Infrastructure

Overview

The most recent and complete infrastructure model documentation is available on Pardee's website. Although the text in this interactive system is, for some IFs models, often significantly out of date, you may still find the basic description useful to you.

The current version of the infrastructure model within IFs was developed in concert with the production of Building Global Infrastructure, the fourth volume in the Patterns of Potential Human Progress series (Rothman et al 2013). Further details on the model and analyses can be found in that volume.

The purpose of the infrastructure model is to forecast the following:

1. the amount of particular forms of infrastructure;
2. the level of access to these particular forms of infrastructure;
3. the level of spending on infrastructure; and
4. the effect of infrastructure development on other socio-economic and environmental systems

The infrastructure model includes parameters that allow users to explore a range of alternative scenarios around infrastructure. These can be used to ask questions such as:

1. What would be the costs and benefits if countries were to accelerate infrastructure development above that seen in the Base Case?
2. What if the unit costs of infrastructure development or infrastructure lifetimes were to differ from the assumptions used in the Base Case?
3. What if the impacts of infrastructure development on economic productivity and health were to differ from the assumptions used in the Base Case? 

Unlike many previous studies, which estimate only the demand for infrastructure, IFs forecasts a path jointly determined by both the demand for infrastructure and the funding available to meet that demand. Therefore, the amount of infrastructure forecasted in IFs in each year explicitly accounts for expected fiscal constraints. Furthermore, the socio-economic and environmental effects of infrastructure feed forward to the drivers of infrastructure demand and supply in future years. 

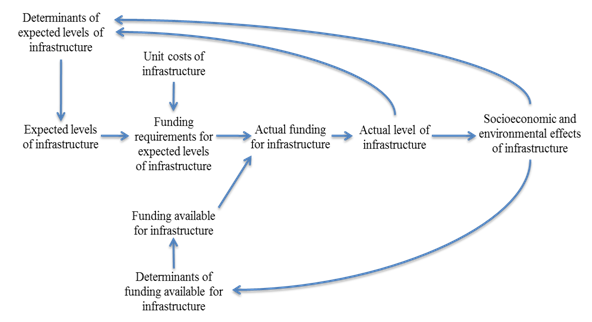
The figure below provides an overview of the infrastructure model within IFs. In brief, the infrastructure modeling in IFs involves moving through the following sequence for each forecast year:

1. Estimating the expected levels of infrastructure
2. Translating the expected levels of infrastructure into financial requirements
3. Balancing the financial requirements with available resources
4. Forecasting the actual levels of attained infrastructure
5. Estimating the social, economic, and environmental impacts of the attained infrastructure 

Each of these steps are described in more detail below.

Structure and Agent System: Infrastructure

System/Subsystem	Infrastructure
Organizing Structure
Stocks	Physical infrastructure, Access rates
Flows	Spending (public and private on ‘core’ infrastructure; public on ‘other’ infrastructure)
Key Aggregate  Relationships  (illustrative, not comprehensive)	Demand for physical infrastructure and access changes with population, income, and other societal changes   More infrastructure helps economic growth and reduces health effects from specific diseases   Public spending available for infrastructure rises with income level   Public spending leverages private spending   Lack (surplus) of public spending on ‘core’ infrastructure hurts (helps) infrastructure development
Key Agent-Class Behavior  Relationships (illustrative, not comprehensive)	Government revenue and expenditure on infrastructure

 

Infrastructure Types

IFs distinguishes between ‘core’ and ‘other’ infrastructure. Core infrastructure refers to those types of infrastructure that we represent explicitly in IFs—roads, electricity generation, improved water and sanitation, and ICT. Other infrastructure refers to those types that we do not represent explicitly—e.g., railroads, ports, airports, and types of infrastructure yet to be envisioned. The choice of what to include as core infrastructure reflects the availability of historical data and understanding of what can be modelled.

Infrastructure Access and Stocks

The table below summarizes the primary variables in IFs related to infrastructure stocks and access. From these and other variables forecasted by IFs, we are able to calculate numerous other indicators—for example, the number of persons with access to electricity.

	Variable Name in IFs (dimensions)	Description	Units
Access	INFRAROADRAI*	Access to rural roads	percentage of rural population living within 2 kilometers of an all-season road
	INFRAELECACC* (rural, urban, total)	Access to electricity	percentage of population with access
	ENSOLFUEL	Solid fuel use	percentage of population using solid fuels as their main household energy source
	WATSAFE* (none, other improved, piped)	Access to improved water	percentage of population with access by type
	SANITATION* (other unimproved, shared, improved)	Access to improved sanitation	percentage of population with access by type
	WATWASTE	Access to wastewater collection connection	percentage of population with wastewater collection
	WATWASTETREAT*	Access to wastewater treatment	percentage of population with wastewater treatment
	INFRATELE*	Fixed telephone lines	lines per 100 persons
	ICTBROAD*	Fixed broadband subscriptions	subscriptions per 100 persons
	ICTMOBIL*	Mobile telephone subscriptions	subscriptions per 100 persons
	ICTBROADMOBIL*	Mobile broadband subscriptions	subscriptions per 100 persons
Physical Stocks	INFRAROAD*	Total road density	kilometers per 1000 hectares
	INFRAROADPAVEDPCNT*	Percentage of roads paved	percentage
	INFRAELECGENCAP*	Electricity generation capacity per capita	kilowatts per person
	LANDIRAREAEQUIP	Area equipped with irrigation	1000 hectares
*Note: Each of these variables has a companion variable with the extension DEM; for example, the variable INFRAROADRAI has a companion variable named INFRAROADRAIDEM. These companion variables indicate the amount of the infrastructure stock or access that would be expected to exist in the absence of financial constraints.

 

Infrastructure Spending

The following table summarizes the primary variables in IFs related to infrastructure spending. As with the access and stock variables, from these and other variables forecasted in IFs, we are able to calculate numerous other indicators—for example, the ratio of total public to private spending on infrastructure. Please note that although we do not represent these other forms of infrastructure explicitly, we do estimate spending on them in order to avoid almost certainly underrepresenting the total demand for infrastructure. This is given by the variable GDS(InfraOther).

Variable Name in IFs	Description	Units
GDS (infrastructure, infraother)	Government consumption, by category[1]	billion dollars
INFRAINVESTMAINT	Total (public plus private) investment for infrastructure maintenance, by type of infrastructure[2]	billion dollars
INFRAINVESTMAINTPUB[3]	Public investment for infrastructure maintenance, by type of infrastructure[2]	billion dollars
INFRAINVESTNEW	Total (public plus private) investment for construction of new infrastructure, by type of infrastructure[2]	billion dollars
INFRAINVESTNEWPUB[3]	Public investment for construction of new infrastructure, by type of infrastructure[2]	billion dollars
[1] The categories are military, health, education, R&D, Infrastructure, InfraOther, Other, and Total. [2] The types of infrastructure included are RoadPaved, RoadUnPaved, ElectricityGen, ElectricityAccRural, ElectricityAccUrban, Irrigation, SafeWaterHH, SafeWaterImproved, SanitationHH, SanitationImproved, WasteWater, Telephone, Mobile, Broadband, BroadbandMobile, and Total. Currently, no cost is assumed for access to Unimproved water, Other unimproved sanitation, solid fuel use, or a wastewater collection connection. [3] Each of these variables has a companion variable, which indicates the amount of public investment that is desired based upon the expected levels of infrastructure.  For INFRAINVESTMAINTPUB, the companion variable is named INFRABUDDEMMNT and for INFRAINVESTNEWPUB, the companion variable is named INFRABUDDEMNEW. The differences between the desired and actual amounts of public investment result from the budgeting process described below. [3] Each of these variables has a companion variable, which indicates the amount of public investment that is desired based upon the expected levels of infrastructure.  For INFRAINVESTMAINTPUB, the companion variable is named INFRABUDDEMMNT and for INFRAINVESTNEWPUB, the companion variable is named INFRABUDDEMNEW. The differences between the desired and actual amounts of public investment result from the budgeting process described below.

 

Forward Links from Infrastructure

Although there are a wide range of potential social, economic, and environmental impacts of infrastructure, we limit our modeling of the direct effects of infrastructure to its effects on economic productivity and a small set of health impacts. Currently, the empirical research on these effects are more advanced—and the effects themselves more amenable to modeling—than the direct effects of infrastructure on factors such as income inequality, educational attainment, or governance. To the extent direct effects and other aspects, such as spending on infrastructure that reduces spending on other categories, affect other systems included in IFs, infrastructure will have a number of indirect effects.

Sources of Infrastructure Data

Infrastructure Stocks and Access

In terms of historical data on infrastructure stocks and access, we can turn to various international organizations with specific emphases. These include the International Road Federation (IRF) for transportation, the International Energy Agency (IEA) for energy, and the International Telecommunication Union (ITU) for telecommunications. No one organization focuses on water and sanitation systems, but a number of different organizations, such as the Joint Monitoring Programme (JMP) of WHO and the United Nations Children’s Fund (UNICEF), the United Nations Statistics Division, and the United Nations Food and Agriculture Organization (FAO), maintain global data related to certain aspects of water infrastructure. The table below summarizes a number of the datasets these groups maintain.

Infrastructure Type	Organization	Spatial Coverage	Temporal Coverage	Infrastructure Coverage
Transportation	International Road Federation	Global	Annual data: 1968–2009	Total road network length, percent of road network paved, and road density
	World Bank	Global	Data for most recent year only	Percentage of rural population with access to an all-season road
Electricity and Energy	United States Energy Information Administration	Global	Annual data: 1980–2010	Total installed electricity generation capacity and generation capacity by energy type
	International Energy Agency	Global	Annual data: 1960–2009	Electricity production by source type; total electricity production; percent of total, urban, and rural population with access to electricity
Water and Sanitation	WHO and UNICEF Joint Monitoring Programme for Water Supply and Sanitation	Global	Annual data: 1990−2010	Percent of population with access to improved, piped, other improved, and unimproved water, and to sanitation facilities
	Food and Agriculture Organization AQUASTAT database	Global	Annual data: 1960–2010	Percent of arable land equipped for irrigation and water use/withdrawals by sector
	United Nations Statistics Division	Global	Data for most recent year available only	Percent of population with wastewater connection and percent with connection to wastewater treatment
Information and Communication Technologies	International Telecommunication Union	Global	Annual data: 1960–2011	Number of telephone mainlines, cell phone subscriptions, broadband subscriptions, mobile broadband subscriptions, and number of computer/internet users

In addition to these primary data sources, the World Bank’s World Development Indicators (WDI) and the World Resources Institute’s Earth Trends databases act as clearinghouses for much of the same data. We can turn also to Canning (1998), Canning and Farahani (2007), and Estache and Goicoechea (2005),who have drawn on these and other sources in attempts to create global databases of infrastructure stocks and access, increase the number of years covered for certain time-series while maintaining consistent definitions, and correct errors. Further, as part of the Africa Infrastructure Country Diagnostic (AICD), the World Bank and the African Development Bank developed an extensive database on infrastructure in Africa. Finally, G. Hughes, Chinowsky, and Strzepek (2009) and Calderón and Servén (2010a; 2010b), among others, have used and modified a number of these databases in their own studies.

Infrastructure Spending

There exist relative little organized historical data on infrastructure spending. In considering public investment in infrastructure (PII), some researchers have used other measures in the Systems of National Accounts, usually fixed capital formation or government outlays by economic sector, as proxies (Agénor, Nabli, and Yousef 2007; Cavallo and Daude 2008; Organisation for Economic Co-operation and Development 2009a; Ter-Minassian and Allen 2004). Lora (2007: 7), however, strongly argued against this practice

because capital expenditures by the central or the consolidated government as measured by the International Monetary Fund’s Government Financial Statistics . . . are a very poor measure of actual PII, which in many countries is mostly undertaken by state-owned enterprises or local governments whose operations are not well captured by this source.

Estache (2010: 67) adds:

Neither the national accounts nor the IMF [International Monetary Fund] Government Finance Statistics (GFS) report a disaggregation of total and public investment data detailed enough to allow identifying every infrastructure sub-sector. In national accounts, energy data cover both electricity and gas but also all primary-energy related products such as petroleum. Similarly, the data do not really distinguish between transport and communication. Water expenditures can be hidden in public works or even in health expenditures.

The World Bank does collect data on private investment in infrastructure in its Private Participation in Infrastructure Project Database. Unfortunately, limitations to this database make us hesitant to rely on it as a primary source of data on infrastructure investment. First, it provides data only on projects in low and middle-income countries in which there is private participation. Second, the amounts in the database primarily reflect commitments, not actual investments. Third, it relies exclusively on information that is made publicly available. Finally, the Bank itself states that it “should not be seen as a fully comprehensive resource.”

This leaves us needing to rely on national, regional, and global studies and reports that provide estimates of infrastructure spending. Given their varied purposes, these studies and reports tend to differ in a number of significant dimensions: temporal coverage; types of infrastructure included; sources of funding (e.g., public versus private); and purpose of expenditure (e.g., new construction versus maintenance). Therefore, we need to be careful in comparing data across studies and in drawing conclusions from them. Even so, they provide a starting point for our exploration. The following table lists a number of these studies and summarizes some of the major elements in their approaches.

Study	Spatial Coverage	Temporal Coverage	Infrastructure Coverage	Source of Funds	Purpose of Expenditure
Trends in Transport Infrastructure Investment 1995–2009 (International Transport Forum and Organisation for Economic Co-operation and Development 2011)	Albania, Australia, Austria, Azerbaijan, Belgium, Bosnia, Bulgaria, Canada, Croatia, Czech Republic, Denmark, Estonia, Finland, , France, Georgia, Germany, Greece, Hungary, Iceland, India, Ireland, Italy, Japan, Korea, Latvia, Liechtenstein, Lithuania, Luxembourg, Macedonia, Malta, Mexico, Moldova, Montenegro, Netherlands, New Zealand, Norway, Poland, Portugal, Romania, Russia, Serbia, Slovakia, Slovenia, Spain, Sweden, Switzerland, Turkey, United Kingdom, United States	Annual data: 1992–2009	Separate data for rail, road, inland waterways, maritime ports, and airports	Combined public and private sources for investment; only spending by public authorities for maintenance	Separate data for investment and maintenance
Africa Infrastructure Country Diagnostic (http://www.-infrastructureafrica.-org/aicd/tools/data) 	Benin, Botswana, Burkina Faso, Cameroon, Cape Verde, Chad, Congo, Côte d’Ivoire, Democratic Republic of the Congo, Ethiopia, Ghana, Kenya, Lesotho, Madagascar, Malawi, Mozambique, Namibia, Nigeria, Rwanda, Senegal, South Africa, Tanzania, Uganda, Zambia	Annual average for one period: 2001–2006	Separate data for electricity, ICT, irrigation, transportation, and water supply and sanitation	Public and private	Separate data for new construction and for operation and maintenance
Infrastructure in Latin America (Calderón and Servén 2010b)	Argentina, Brazil, Chile, Colombia, Mexico, Peru	Annual data: 1980–2006	Separate data for telecommunications, power generation, land transportation (roads and railways), and water and sanitation	Separate data for public and private	Total spending (construction, operations, and maintenance)
Public Spending on Transportation and Water Infrastructure (Congressional Budget Office 2010)	United States	Annual data: 1956–2007	Separate data for highways, mass transit, rail, aviation, water transportation, water resources, and water supply and wastewater treatment	Public only, broken down by (1) federal, and (2) state and local	Separate data for capital expenditures and for operation and maintenance
Infrastructure Development in India and China—A Comparative Analysis (Kim and Nangia 2010)	China, India	Annual data: 1985–2006	Combined data for electricity, water, gas, transport, and communications	Combined public and private	Not stated
Going for Growth: Economic Policy Reforms (Organisation for Economic Co-operation and Development 2009a)	Australia, Austria, Belgium, Canada, Finland, France, Iceland, Ireland, Italy, Netherlands, New Zealand, Norway, South Korea, Spain, Sweden, United Kingdom, United States	Annual averages for four periods: 1970–1979, 1980–1989, 1990–1999, 2000–2006	Aggregate data provided separately for (1) electricity, gas, and water, and (2) transport and communications	Combined public and private	Aggregate investment (from national accounts)
Connecting East Asia: A New Framework for Infrastructure (Asian Development Bank, Japan Bank for International Cooperation, and World Bank 2005)	Cambodia, China, Indonesia, Laos, Mongolia, Philippines, Thailand, Vietnam	Annual data for select years: 1998, 2003	Separate data for transportation, telecommunications, water and sanitation, other urban infrastructure, and power	Separate data for national government, local government, state owned enterprises, and private	Not stated

Dominant Relations: Infrastructure

The dominant relations in the Infrastructure model are those that determine the expected levels of infrastructure stocks and access, spending on infrastructure, and the impacts of infrastructure on health and productivity. The expected levels of infrastructure stocks and access are influenced by socio-economic factors related to population, economic activity, governance, and educational attainment. In almost every case there are also path dependencies that supplement the basic relationships, reflecting the considerable inertia in infrastructure development.

Spending on infrastructure is divided into private and public spending, with the latter further divided into ‘core’ and ‘other’ infrastructure. ‘Core’ infrastructure refers to those types of infrastructure that are explicitly represented in the model; ‘other’ infrastructure refers to those types of infrastructure that are not explicitly represented in the model (see Infrastructure Types). Public spending on core infrastructure, GDS(Infra), is driven by the required spending to meet the expected levels of infrastructure (INFRABUDDEMMNT and INFRABUDDEMNEW), total government consumption (GOVCON), and the demands on government consumption from other categories. Public spending on other infrastructure, GDS(InfraOther), is driven by average GDP per capita (GDPPCP), total government consumption (GOVCON), and the demands on government consumption from other categories. Deficits and surpluses of government funds will affect the actual levels of funds allocated for both core and other infrastructure. The public spending on core infrastructure leverages a certain amount of private spending on core infrastructure, with the amount leveraged depending upon historical relationships found in the literature, which nominally reflect the variation in public and private returns between particular types of infrastructure. Finally, in recognition of the incremental approaches that public budgeting decisions usually follow, our model avoids unusually sharp increases in public spending on infrastructure by smoothing it out over time.

Infrastructure development directly affects multifactor productivity, with this effect being treated separately for non-ICT and ICT related infrastructure. The use of solid fuels in the home and access to improved water and sanitation directly affect human health through their effects on the mortality and morbidity rates of specific diseases—diarrheal diseases, acute respiratory infections, and respiratory diseases.

For detailed discussion of the model's causal dynamics, see the discussions of flow charts (block diagrams) and equations.

Initializing the Infrastructure Data

The IFs preprocessor uses historical data to prepare data for the base year of the model, currently 2010. We describe the general workings of the IFs preprocessor here. However, there are some peculiarities in the infrastructure model, specifically related to the initialization of the variables related to spending on infrastructure.

Because of the paucity and inconsistency of the historical data on infrastructure spending discussed above, IFs does not use actual historical data on spending, but rather estimates spending in the first year of the model based upon data on the stocks of and access to infrastructure after the pre-processor has filled any gaps in the historical data. The procedure is as follows:

• We assume that: 1) the amount of infrastructure requiring maintenance in the base year is given by the level of infrastructure in the previous year (2009) times a factor based on the lifetime of the infrastructure (see table 5 below), and 2) the amount of newly constructed infrastructure is the difference between the amount of infrastructure in the base year (2010) and the previous year (2009).
• Total spending on maintenance, INFRAINVESTMAINT, is estimated as the amount of infrastructure requiring maintenance times the unit cost for each type of infrastructure (see Table 6 below).
• Total spending on new construction, INFRAINVESTNEW, is estimated as the amount of new construction times the unit cost for each type of infrastructure. If the amount of newly constructed infrastructure is less than or equal to zero, spending on that type of infrastructure is set to zero.
• For each type of infrastructure, public spending on maintenance, INFRAINVESTMAINTPUB, and new construction, INFRAINVESTNEWPUB, are estimated by multiplying the total spending by infrastructure specific parameters, infrainvmaintpubshrm and infrainvnewpubshrm , indicating the share of total spending that is assumed to be public.
• The sum of estimated public spending on maintenance and new construction, across all types of core infrastructure, provides an initial estimate of government consumption for core infrastructure, GDS(Infrastructure).
• If, in the first year budgeting process, total estimated government consumption on core infrastructure is reduced, an infrastructure cost adjustment factor, INFRACOSTADJFAC, is calculated as the ratio of the final to the initial value of GDS(Infrastructure). The value of INFRACOSTADJFAC is also used to adjust infrastructure spending in future years. It gradually converges to 1 over the time period given by the parameter infracostadjfacconvtime .
• The initial estimates of INFRAINVESTMAINT, INFRAINVESTNEW, INFRAINVESTMAINTPUB, and INFRAINVESTNEWPUB are each multiplied by INFRACOSTADJFAC to calculate their final values.
• The initial value of public spending on other infrastructure, GDS(InfraOther ), is calculated as a function of average income, GDPPCP, multiplied by INFRACOSTADJFAC. This function is:

 

$GDS(InfraOther)_{r,t}=GDP_{r,t}*(1.8162+0.061*ln(GDPPCP_{r,t})$

GDS(InfraOther) = government spending on other infrastructure in billion constant 2005 dollars

GDP = gross domestic product at market exchange rates in billion constant 2005 dollars

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

Infrastructure Flow Charts

Overview 

The introduction provided an overview of the infrastructure model within IFs, noting that this involves moving through the following sequence for each forecast year. This section describes each of these five steps: 

1. Estimating the Expected Levels of Infrastructure

At the core of our forecasts of the expected levels of infrastructure is a set of estimated equations embedded within a set of accounting relationships. The equations are presented here.

Additional elements beyond the estimated equations are involved in specifying the expected values of infrastructure, and we handle some of these elements algorithmically. For instance, the base year calculated estimations will most often not match exactly the historical data for countries in the base year.^[1] Each country has peculiarities that differentiate it from the “typical pattern”; among the factors not captured by our equations for estimating the base year country values are many aspects of geography, culture, and unique historical development paths. And sometimes, of course, data errors account for such differences.

To deal with this issue of differences between our estimated values and reported data in the base year, the model calculates an additive or a multiplicative country and variable specific shift factor representing that difference; we allow those shift factors to gradually diminish over time, thereby causing countries to approach the expected value function. Among the reasons for allowing convergence is that we quite consistently see that the patterns of higher-income countries are more similar and more like those of our general equations than are those of lower-income countries. On the assumption that countries will seldom abandon infrastructure they have already developed, however, our downward convergence is extremely slow relative to our upward convergence.

A second instance in which we make adjustments to our core estimated equations is when the dynamic trajectory of demand/supply growth in a country in recent years is inconsistent with the forecasts produced by the equations. For instance, a policy-based surge of infrastructure development like that seen recently in China may result in a historical growth rate well above the one that our functions produce in the first years of our forecasting. Making a simplifying assumption that these growth rates will change only gradually, we estimate the growth rate of physical infrastructure stock using the historical data over three to five recent years and incorporate that growth rate in the demand estimation through a moving average-based extrapolative formulation.

We make a final adjustment in those cases where we wish to modify the estimates of expected infrastructure for scenario analysis. This can be accomplished in several ways. First, most of the estimates can be adjusted with the use of a simple multiplier. Second, we can stipulate specific levels for specific types of infrastructure in a specific future year; in this case, the model will automatically forecast a linear approach to the targeted level from the base year. Third, we can modify both the rates at which the country shift factors converge and the levels, in relation to the expected values, to which the shift factors converge. For example, we can drive the shift factors to those of the best performing countries, i.e., those that perform better than expected, by a certain date. This will, in turn, affect the levels to which the physical infrastructures themselves converge (see Standard Error Targeting).

Transportation

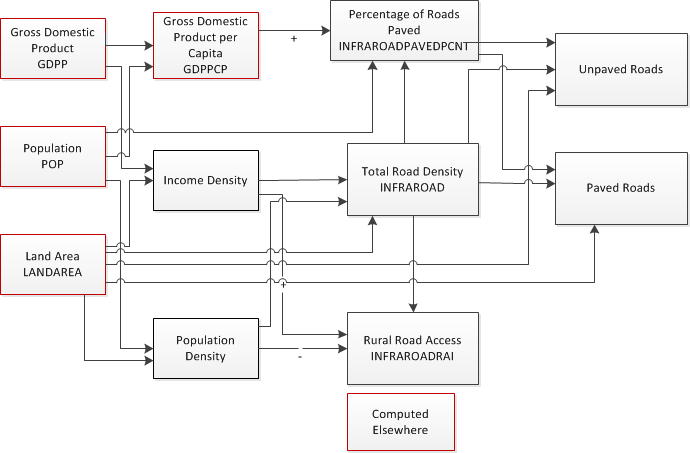
The primary indicators of transportation infrastructure included in IFs are: 1) the total road density in kilometers per 1000 hectares, INFRAROAD, 2) the percentage of roads that are paved, INFRAROADPAVEDPCNT, and 3) the Rural Access Index, INFRAROADRAI, the percentage of the rural population living within two kilometers of an all-season road. From these, we can calculate additional indicators, such as the expected lengths of paved and unpaved roads.

The general sequence of calculations for estimating the expected values of these variables is shown in the figure below. We begin by estimating road density (INFRAROAD) as a function of income density, population density, and land area. The percentage of roads that are paved (INFRAROADPAVEDPCNT) is then calculated as a function of the estimated road density, GDP per capita (GDPPCP), population (POP), and land area (LANDAREA). In parallel, the Rural Access Index(INFRAROADRAI) is calculated as a function of the estimated road density (kilometers per person) and income density (dollars per hectare).

Electricity

Our focus in the energy sector is on the generation and use of electricity. In terms of physical infrastructure, the key indicator we forecast is the level of electricity generation capacity, INFRAELECGENCAP. From the user perspective, we forecast the percentage of the rural and urban populations that have access to electricity, INFRAELECACC(rural) and INFRAELECACC(urban). These access rates, in combination with the forecasts for population and average household size, are used to calculate the number of household connections, which drive the cost calculations described below. Finally, given its connection to electricity access, we also forecast the percentage of the population that uses solid fuels as the main source of energy, ENSOLFUEL. At the moment, no physical infrastructure is associated with solid fuels, so this value does not enter into the cost calculations.

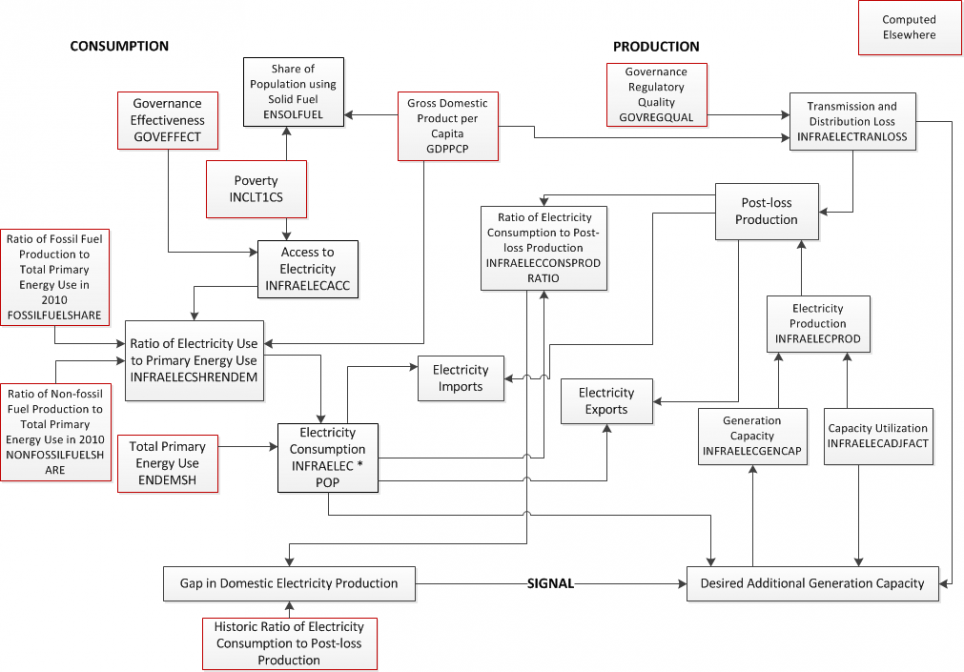
The following figure presents an overview of the submodel that forecasts access to electricity and electricity generation capacity in IFs. It is fully integrated with the larger IFs system, which provides forecasts of critical variables such as energy demand, energy production by primary type, poverty, and governance character. The electricity submodel contains three components—estimating consumption, estimating production, and sending a signal for additional generation capacity in the case of a gap between production and consumption.

Beginning with consumption, we first estimate the percentage of the population with access to electricity (INFRAELECACC). This is forecast as a function of poverty levels (INCOMELT1CS/POP) and a measure of government effectiveness (GOVEFFECT). The levels of access, along with average income (GDPPCP) determine the share of the population using Solid Fuel for heating and cooking (ENSOLFUEL). Next, the levels of access and average income (GDPPCP), along with the historic ratios of fossil fuel and non-fossil fuel production to total primary energy use (FossilFuelShare and NonFossilFuelShare), are used to forecast the expected ratio of electricity use to total primary energy use (INFRAELECSHRENDEM). With this ratio and the level of total primary energy use (ENDEMSH)^[2], forecast elsewhere in IFs, we then calculate the desired electricity use (INFRAELEC * POP).

The amount of domestically produced electricity (INFRAELECPROD) is determined by the existing generation capacity (INFRAELECGENCAP), adjusted by a capacity utilization factor (INFRAELECTADJFACT). We estimate the initial capacity utilization factor for each country based on historical data related to generating capacity and electricity production. Over the forecast horizon, the capacity utilization factor is assumed to converge, over a 50 year period, to a global average value, 0.55, which we derived from current data on generation capacity and production in high-income countries. We also account for transmission and distribution loss (INFRAELECTRANLOSS), which we forecast as a function of average income (GDPPCP) and a measure of governance regulatory quality (GOVREGQUAL). This allows us to calculate post-loss production of electricity.

The desired electricity use can be met by either the domestic post-loss production or imports. Similarly, the post-loss production can be used for either domestic use or exports. At the moment, we assume that the imports are available, when necessary, and that any excess post-loss production can be exported; i.e., we do not attempt to balance the trade in electricity. In parallel, we use the ratio of desired electricity use to post-loss production (INFRAELECCONSPRODRATIO) as a driver of future levels of generating capacity. Each year the computed ratio is compared to a historical value calculated in the pre-processor. We make the simplifying assumption that countries wish to keep this ratio constant over time. A growing ratio implies that domestic consumption is increasing at a faster rate than domestic production, which sends a signal indicating a desire to build additional capacity. A declining ratio implies that domestic consumption is increasing at a slower rate than domestic production. While this could send a signal to remove existing capacity, the model does not do so; rather it calls for no new construction and less than full replacement of depreciated capacity. Over time, this should bring the production and use back into historical balance.

 

Water and Sanitation

Access to Water, Access to Sanitation, and Wastewater Treatment

The key access indicators we include for water and sanitation infrastructure are the percentages of the population with access to different levels of improved drinking water and sanitation and whose wastewater is collected and subsequently treated. The physical quantities include the number of connections providing these services and the amount of land that is equipped for irrigation.

We originally introduced forecasts of access to improved sources of drinking water and sanitation into IFs in support of the third volume in the PPHP series, Improving Global Health (Hughes, Kuhn, et al. 2011), because of the health risks associated with a lack of clean water and/or improved sanitation. We have extended this portion of the model to include forecasts of the share of wastewater that is collected and then treated prior to being returned to the environment. In addition, we have added a component to forecast the area equipped for irrigation.

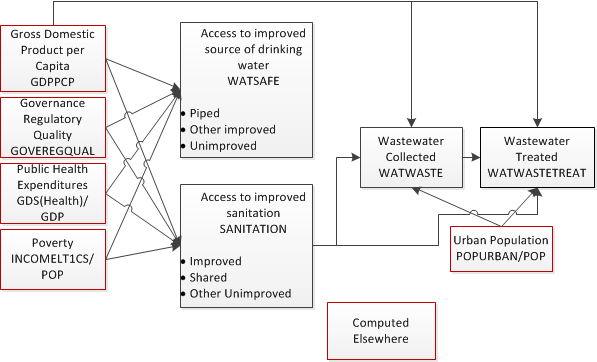
The WHO and UNICEF (2013) use the concept of “ladders” for drinking water sources and sanitation systems. They currently include four steps for both drinking water (surface water, unimproved, other improved, and piped on premises) and sanitation (open defecation, unimproved, shared, and improved). As countries develop, more of their citizens ascend these ladders. We have combined these into three categories each; for drinking water these are unimproved, other improved, and piped; for sanitation, these are other unimproved, shared, and improved. Notably, using international standards, estimates of the total population with access to improved sanitation does not include the shared category.

We forecast the shares of the population in each of the water and sanitation ladder categories using average income, poverty levels (measured as the percentage of the population living on less than $1.25 per day), educational attainment (measured as the average number of years of formal education for adults over 25), and public health expenditures as explanatory variables (see the next figure). These results then feed into the forecasts of the percentage of population with wastewater collection and wastewater treatment.

Finally, these access rates, in combination with the forecasts for population and average household size, are used to calculate the number of safe water, sanitation, and wastewater treatment connections, which drive the cost calculations described below.

Area Equipped for Irrigation

There have been few forecasts of the area equipped for irrigation, and those that do exist tend to be based on very detailed analyses of specific situations. In a recent report from the United Nations Food and Agriculture Organization (FAO) looking out to the year 2050, Bruinsma (2011: 251) stated that the “projections of irrigation presented in this section are based on scattered information about existing irrigation expansion plans in different countries, potentials for expansion (including water availability) and the need to increase crop production.” Another report looking at global agriculture over the next half century (Nelson et al. 2010), this one from the International Food Policy Research Institute, relies on exogenous assumptions of the growth in irrigated area. The authors do not specify the source of these assumptions, but some of the same authors (You et al. 2011) have reported on the irrigation potential for Africa, basing their conclusions on agronomic, hydrological, and economic factors.

Rather than attempt to replicate the level of detailed analysis of most previous studies, we forecast the area equipped for irrigation based on data from the FAO’s FAOSTAT and AQUASTAT databases on historical irrigation patterns and the area that could potentially be equipped for irrigation. These data are incomplete; for area equipped for irrigation, data are provided for 168 of the 186 countries included in IFs, and for the potentially irrigable area, data are provided for 117 of 186 countries. In our examination of these historical data, we found that a number of countries had already reached an apparent plateau in the amount of area equipped for irrigation that was often well below the potential indicated. For example, Argentina’s equipped area has stayed at a bit over 1.5 million hectares since the late 1970s, even though its potential is given as more than 6 million hectares. Why a country saturates below its ultimate potential is often unclear, but one obvious reason for some countries is that they receive enough rainfall to not warrant further irrigation.

In any case, once we have determined an appropriate saturation level for each country and a recent historical growth rate, we assume that the expected area equipped for irrigation gradually approaches the saturation level. The rate of growth starts at the historical growth rate, with the growth rate slowing as the saturation level is approached. The user can modify this path using the parameter ladirareaequipm , which acts as a multiplier. Still, the amount of area equipped for irrigation cannot exceed the specified saturation level for the country.

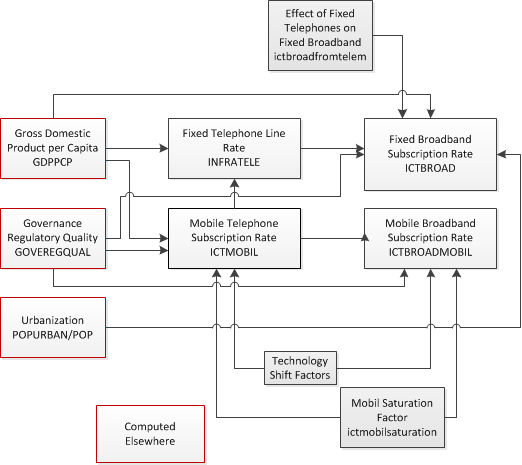
ICT

We forecast four basic indicators of ICT infrastructure: fixed telephone lines, fixed broadband subscriptions, mobile telephone subscriptions, and mobile broadband subscriptions, all per 100 persons. Our forecasts for the expected levels of these different forms of ICT infrastructure are driven in part by cross-sectional relationships with average income and government regulatory quality. As the next figure illustrates, however, there are also interactions among the different forms of ICT.

For each technology, we found strong relationships indicating that usage levels (our proxies in this case for access) increase with rises in average income and governance regulatory quality; in the case of fixed broadband, we also found urbanization to be important, as one might expect for a technology whose installation is supported by population density.

As for the interactions between the different forms of ICT, we start with fixed telephone lines. Given the potential for substitution by mobile telephone lines, we assume that the demand for fixed telephone lines will decline as mobile usage increases. Already we see this happening in the data, especially, but not exclusively, in high-income countries. Our analysis of the historical data indicates a level of approximately 30 mobile telephone subscriptions per 100 persons as the point at which fixed-line telephone decline begins, so we build this into our forecasts algorithmically. We do not expect that fixed telephone line usage will completely disappear. Rather, we assume arbitrarily that it will settle at a low level; this is set by default to 2.5 lines per 100 persons. Furthermore, we also assume that: (1) mobile broadband subscriptions will never exceed mobile telephone subscriptions; and (2) any decline in fixed telephone lines will boost the growth in fixed broadband because countries that have existing investments in fixed-line infrastructure are able to leverage these networks to provide broadband access with rather modest investments.

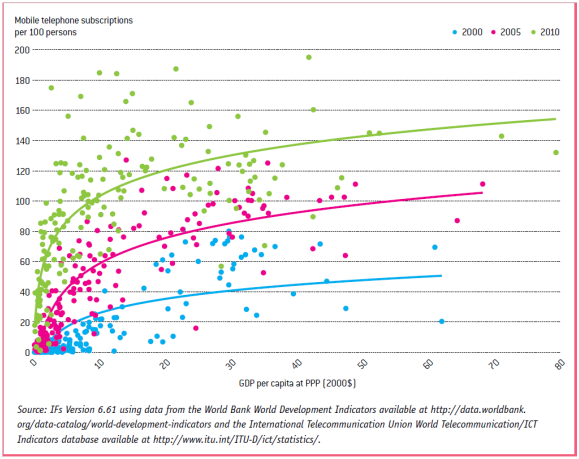
The cross-sectional relationships with income do not remain static across time for mobile phones, fixed broadband, and mobile broadband. The last figure shows this for mobile telephone subscriptions. The individual points reflect historical data for country access rates for the years 2000, 2005, and 2010. The lines are logarithmic curves fit through these data. The upward shift over time reflects advances in information and communication technologies that are making ICT cheaper and more accessible around the world. These advances are, in turn, driven by various systemic factors ranging from product and process innovation to network effects.

In order to capture the effect of this rapid change in our forecasts of future access, we combine the use of the cross-sectional function with an algorithmic approach that simulates the upward shift of the curves for mobile phones, fixed broadband, and mobile broadband. The algorithmic element assumes a standard technology diffusion process in which the growth in penetration rate associated with the technological shift rises from a low annual percentage point increase at low levels of penetration to a maximum at the middle of the range (the inflection point) and falls again as saturation is approached. For each of the three technologies, we have looked at historical patterns to estimate the minimum and maximum growth rates, expressed as annual percentage points of absolute change.

The choice of saturation levels is obviously quite important. Data from the International Telecommunications Union show penetration rates for mobile phones that exceed 100 subscriptions per 100 persons (e.g., approaching 200 in Hong Kong). At the same time, some countries (e.g., Denmark) seem to be reaching a saturation level for fixed broadband well below 100 subscriptions per 100 persons. Uncertainty remains over the proper level of saturation to assume for these subscriptions, and therefore, different researchers use different values. Specifically, we define saturation as 50 subscriptions per 100 persons for fixed broadband and 150 subscriptions per 100 persons for both mobile technologies. In addition, we assume that mobile broadband penetration cannot exceed mobile phone penetration.

Similarly to the other access rates, the numbers of lines and subscriptions per 100 persons, in combination with the forecasts for population, are used to calculate the absolute number of lines and subscriptions, which drive the cost calculations described in the diagram below.

---

[1] Not all countries have data for all indicators included in the model in the base year. IFs includes a preprocessor that uses a series of algorithms that draw on historical data for previous years, the estimated equations, and other factors to initialize these missing data.

[2] ENDEMSH is an adjusted value of ENDEM, which takes into account the differences between the base year values for total primary energy use from historic data and the base year values calculated in the pre-processor, which adjusts for differences between the physical and financial data on energy trade. The ratio of ENDEMSH to ENDEM gradually converges to 1 over a number of years given by the parameter enconv .

2. Translating the Expected Levels of Infrastructure into Financial Requirements

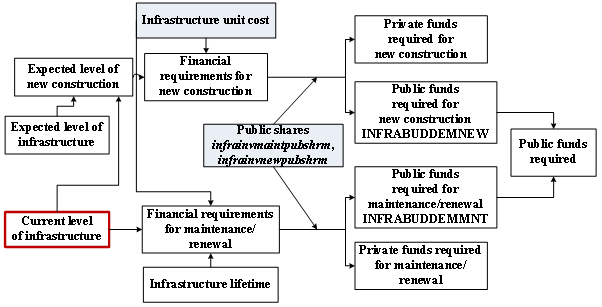
In estimating the financial requirements to achieve the expected levels of infrastructure, we adopt the approach introduced by Fay (2001) and Fay and Yepes (2003) described earlier. In this approach, there are two components to the financial requirements for each type of infrastructure each year. First there is the cost of maintenance/renewal of existing infrastructure. Second, there is the cost of new construction. These then need to be separated into public and private shares. The following figure shows the general process for each type of infrastructure.

Estimating the financial requirements for new construction

For each type of infrastructure, the existing level of physical infrastructure is subtracted from the forecasted level and the difference is multiplied by the unit cost (see the table below for the list of the parameters that store the information on the unit costs). The results are then summed across the different types of infrastructure to calculate the total demand for funding for new construction. In a slight variation, rather than calculate the growth of the physical stock, Stambrook (2006) first calculated the asset value of the existing road stock by multiplying the level of the physical stock by a unit cost. He then directly forecasted the growth of this asset value, which was assumed to be equal to the investment requirements.

Estimating the financial requirements for maintenance/renewal

Although we use the term “maintenance” for this second set of infrastructure funding requirements, different studies use different nomenclature. Bhattacharyay (2010), Fay and Yepes (2003), Kohli and Basil (2011), and Yepes (2005), all use “maintenance”; Chatterton and Puerto (2006) refer to “rehabilitation.” Yepes (2008) refers to “maintenance and rehabilitation.” Finally, G. Hughes, Chinowsky, and Strzepek (2009) provide separate estimates for replacement and for maintenance. In general, however, the methodology for the estimation of the funding requirements is the same across all studies. For each type of infrastructure, the funding is determined as a percentage of the dollar value of the existing infrastructure. The dollar value is given as the amount of infrastructure in physical units multiplied by the same unit cost used for estimating the funding for new construction. The percentage is based on the average lifetime of the particular infrastructure (see Table 6 for the list of the parameters that store the infrastructure lifetimes in IFs). Fay and Yepes (2003: 10) referred to this as “the minimum annual average expenditure on maintenance, below which the network’s functionality will be threatened.” Later authors have more specifically related the percentage to the depreciation rate or average expected lifetime of each type of infrastructure (Chatterton and Puerto 2006; Yepes 2005, 2008).

Separating the financial requirements into public and private shares

In the real world funding for infrastructure comes from both public and private sources, so we separate the funding requirements into public and private components. We assume a specific share of public and private funding for each type of infrastructure. This, in effect, implies that public spending on infrastructure leverages a certain amount of private spending. These shares differ by type of infrastructure, but are constant across countries and time. The share parameters are infrainvmaintpubshrm and infrainvnewpubshrm , each of which is a vector, with the dimension representing the type of infrastructure. The balancing of the financial requirements with the available resources included in IFs and described in the next section only considers the public sector.

Infrastructure Type (unit)	Unit Cost Parameters[1]	Lifetime Parameter
Paved road (kilometer)	infraroadpavedcostlower, infraroadpavedcostm, infraroadpavedcostupper	infraroadpavedlife
Unpaved road (kilometer)	infraroadunpavedcostlower, infraroadunpavedcostm, infraroadunpavedcostupper	infraroadunpavedlife
Electricity generation (megawatt)	infraelecgencostlower, infraelecgencostm, infraelecgencostupper	infraelecgenlife
Rural electricity (connection)	infraelecaccruralcostlower, infraelecaccruralcostm, infraelecaccruralcostupper	infraelecaccrurallife
Urban electricity (connection)	infraelecaccurbancostlower, infraelecaccurbancostm, infraelecaccurbancostupper	infraelecaccurbanlife
Irrigation equipment (hectare)	landircostlower, landircostm, landircostupper	landirlife
Improved water (connection)	watsafeimpcostlower, watsafeimpcostm, watsafeimpcostupper	watsafeimplife
Piped water (connection)	watsafecostlower, watsafecostm, watsafecostupper	watsafelife
Shared sanitation (connection)	sanitationimpcostlower, sanitationimpcostm, sanitationimpcostupper	sanitationimplife
Improved sanitation (connection)	sanitationcostlower, sanitationcostm, sanitationcostupper	sanitationlife
Wastewater treatment (connection)	watwastetreatcostlower, watwastetreatcostm, watwastetreatcostupper	watwastetreatlife
Fixed telephone (line)	infratelecostlower, infratelecostm, infratelecostupper	infratelelife
Fixed broadband (subscription)	ictbroadcostlower, ictbroadcostm, ictbroadcostupper	ictbroadlife
Mobile phone (subscription)	ictmobilcostlower, ictmobilcostm, ictmobilcostupper	ictmobillife
Mobile broadband (subscription)	ictbroadmobilcostlower, ictbroadmobilcostm, ictbroadmobilcostupper	ictbroadmobillife
[1] The actual unit costs can change as a function of GDP per capita (GDPPCP). For a given type of infrastructure, below a given level of GDPPCP, the unit cost takes on the value specified by the parameter ending with ‘lower’. Above a given level of GDPPCP, the unit cost takes on the value specified by the parameter ending with ‘upper’. Between these two values of GDPPCP, the unit cost changes in a linear fashion between the ‘lower’ and ‘upper’ value as a function of GDPPCP. Currently, the lower and upper thresholds for GDPPCP are hard coded in the model and vary by type of infrastructure. [2] The unit cost parameters ending in ‘m’ are multipliers that can be used to change the unit cost directly. [3] As described in the discussion on initializing the infrastructure data for IFs, the unit costs are also multiplied by the variable INFRACOSTADJFAC, which is calculated in the first year of the model as part of balancing the government spending in that year. This variable always has a value between 0 and 1, and gradually converges to 1 over the time period given by the parameter infracostadjfacconvtime .

3. Determining the Actual Funds for Infrastructure Spending

There is no guarantee that the requirements for infrastructure funds will match those made available. In determining whether this is the case, we focus on the public spending for infrastructure. In IFs, government domestic revenues and net foreign aid are summed into government expenditure (GOVEXP), which is then allocated between transfers, (GOVHHTRN - pensions and other social payments) and direct government spending (GOVCON). The latter is divided among broad categories— defense, education, health, research and development, core infrastructure, other infrastructure, and a residual category of other government spending. It is through this process of allocating government revenues that the amount of public funding for infrastructure ultimately is determined. IFs allows some imbalance between revenues and total expenditures year to year, but neither debt nor surpluses can accumulate indefinitely; as their percentages of GDP change, signals adjust revenues and expenditures over time.

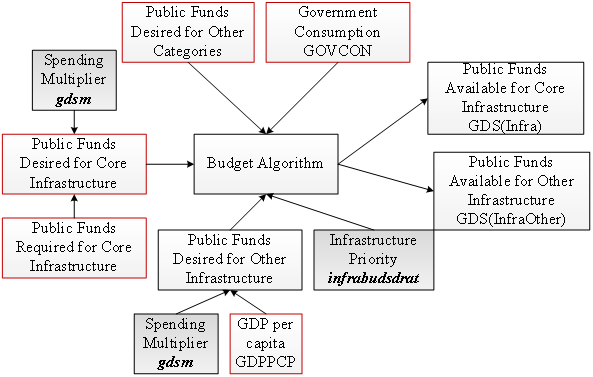
The figure below illustrates how the actual public funds available for core infrastructure are determined starting from the public funds required for core infrastructure estimated in the previous step. During this step, the amount of public funds available for other infrastructure is also determined.

Prior to the budget algorithm, the public funds required for core infrastructure can be modified by a spending multiplier, gdsm(Infrastructure) , to determine the public funds desired for core infrastructure. Similarly, the public funds desired for other infrastructure, which are initially estimated as function of GDP per capita, can be modified by a spending multiplier, gdsm(InfraOther ). Finally, the parameter infrabudsdrat can be used to indicate the priority that should be given to core and other infrastructure in the budget allocation process (it affects both categories equally).

The budget algorithm takes this information, along with the public funds desired for other categories and government consumption to determine the public funds available for core and other infrastructure. First, a fraction, defined by infrabudsdrat divided by 1, of the public funds desired for core and other infrastructure, up to the level of total government consumption, is allocated to these categories and removed from total government consumption (there is a similar parameter, edbudgon , discussed in the Education section of the Help system). The remaining government consumption is allocated to the various categories based upon their desired levels of funding (at this point, the amounts of desired funding for core and other infrastructure does not include the amounts already set aside). In the case of demand-supply mismatches, the subtractions or additions are allocated to each category based on their relative shares of the total desired funding. There is also a minimal level of funds allocated to each category; i.e., each category will receive at least some funds. (Note, the budget allocation process is described in more detail in the governance section of this Help system.)

4. Determining the Forecasted Levels of Infrastructure Spending and Attainment

Once the level of public funds available for core infrastructure is determined, we can forecast the levels of infrastructure that will be attained. If there is a match between the estimated funding requirements and the estimated funding available, the process is fairly straightforward. In the case where there is a demand-supply mismatch, the forecasting becomes more complicated. The following figure presents this process.

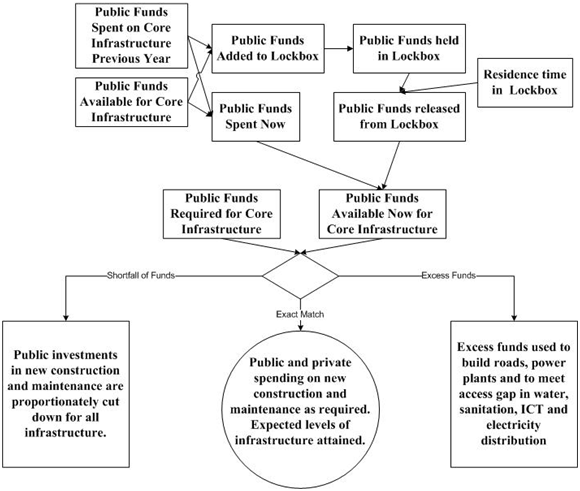
Recognizing that the infrastructure sector may not be able to manage rapid increases in public funding, we first smooth the actual provision of the public funds. Specifically, if the public funds available in the current year dramatically exceed the amount spent in the previous year, a portion of the available funds are held in reserve (in a lockbox). The threshold for this increase is half a percent of GDP. The funds in the lockbox are gradually released over time. The amount released from the lockbox depends on the amount in the lockbox and a fixed coefficient, InfraSpndBoxUnloadFactor, indicating the fraction that can be released in any year. This value is currently hard coded at 0.2. The amount of public funds available in the present year for core infrastructure is, therefore, the sum of the public funds coming out of the budget process for the current year not put in reserve plus the funds released from the lockbox in the current year. This amount is then compared to the public funds required for core infrastructure determined previously.

In the case of an exact match between the public funds available in the present year for core infrastructure exactly matches the public funds required, the amounts of public and private spending on new construction and maintenance/renewal are exactly the amounts required. Similarly, the levels of infrastructure attained exactly match those expected (see again earlier figures on expected levels of infrastructure).

In the case of a budget shortfall, we make three simplifying assumptions. First, we assume that all forms of infrastructure are affected equally; specifically, each receives the same proportionate cut in the amount of public funding received. Second, with the exception of ICT infrastructure (fixed and mobile telephones and broadband), we assume that the amount of private funding is reduced by the same proportion. This is based on our premise, stated earlier, that public funding for infrastructure leverages private spending, so less public funding also means less private spending. We make the exception for ICT because this is a less-tenable assumption for that sector given the degree to which private spending historically has driven ICT development. Specifically, private funding for ICT is not reduced even in the case of a reduction of public funding. Third, we assume that the reductions in funding affect spending on both maintenance and new construction equally. The net result is that there will be less new construction of infrastructure than desired, as well as less maintenance of existing infrastructure. This can lead to an absolute decline in some forms of infrastructure when the new construction is not enough to make up for the amount of infrastructure lost due to inadequate maintenance.

This is slightly altered when targets are set for infrastructure. Here, an algorithm is used that first tries to ensure that the funds are used to provide the levels of construction and maintenance implied by the expected values estimated in the absence of a target. In this way, infrastructures with high targets are not favored over other forms of infrastructure. Any remaining funds are then distributed among all other infrastructure types, with their shares being proportional to the funds required to achieve the expected levels of construction and maintenance implied by the target.

A further effect of a budget shortfall is that when infrastructure stocks do not achieve their expected levels, there is a feedback to our access measures.

When there is a budget surplus, the extra funds go to additional new construction because the maintenance/renewal requirements are already covered. The surplus is spread across the different forms of infrastructure using the following logic. First, r oads and electricity generation are allocated shares of the excess funds determined by their historical shares in total infrastructure spending. Second, the remainder of the excess funds is disbursed among the infrastructures that involve access. They are used to meet the gap to universal (stipulated) access rate with a cap on how much of the gap can be met each year. Private funding is not affected by increases in public funding from “surplus funds.”

Estimating the Social, Economic, and Environmental Impacts of the Attainable Infrastructure

There a number of possible social, economic, and environmental impacts of infrastructure. We divided these into impacts on economic growth, income distribution, health, education, governance, and the environment. Given the limited empirical support for many of these linkages and, thus, a high level of uncertainty about whether and how to represent them, we have limited our inclusion of direct links from infrastructure to the links from infrastructure to economic growth and health. Important indirect linkages supplement the direct linkages that we describe here. For example, the forward linkages from economic growth to environmental impact (via paths such as increased energy use and food demand) and from improved health to demographic change are present in the current model. In fact, the indirect linkages via both of these paths are pervasive across the model.

Impacts on productivity and economic growth

We estimate the impact of infrastructure on economic growth through its effect on multifactor productivity. Most economic models relate aggregate growth to changes in factors of production, typically capital (K) and labor (L), and an additional component, which is variously called the Solow residual, the technological change parameter, total factor productivity (TFP) or multifactor productivity (MFP); here we use the MFP label. Analyses have long shown that MFP can be quite large (Solow 1956; 1957). Within IFs, we treat MFP as an endogenous variable that human capital, social capital, physical capital, and knowledge capital influence (Hughes 2007). Infrastructure is a key component of physical capital, along with natural resources. The impact of the latter is represented through the effect of energy prices on MFP.

In estimating the impact of infrastructure on MFP, we relate the impact to measures of physical infrastructure and not to measures of infrastructure spending. Because of the interaction effects across infrastructure types, we do not attempt to estimate the impact of individual forms of infrastructure but rather estimate the impact as a function of a composite index of infrastructure. Due to the very different historical and expected growth patterns of more traditional infrastructure—transportation, energy and water—vis-à-vis ICT, we create a separate index for ICT and link it to the physical capital component of MFP (MFPPC) in a different way.

Traditional Infrastructure – Transportation, Electricity, and Water and Sanitation

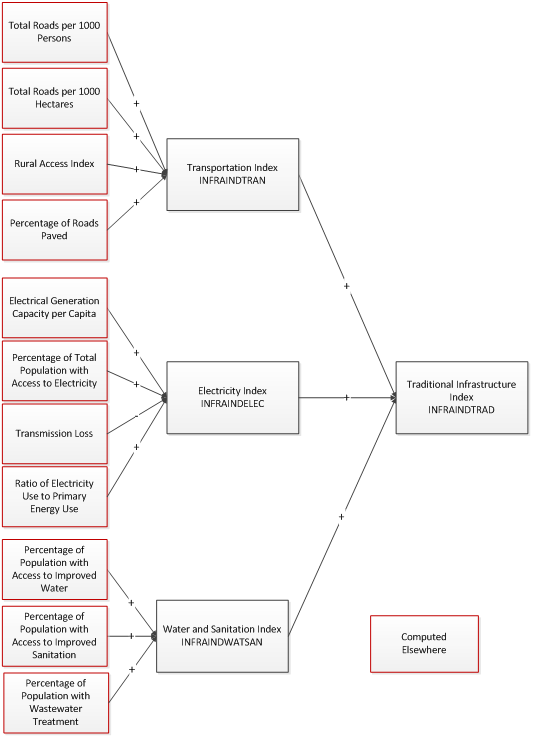
For the more traditional forms of infrastructure—transportation, electricity, and water and sanitation, we first construct a set of component indices—INFRAINDTRAN, INFRAINDELEC, and INFRAINDWATSAN (see the figure below). These are then aggregated into an overall index, INFRAINDTRAD.

In order to construct these indices, we followed the approach presented in Calderón and Servén (2010a). This begins with basic measures of infrastructure, e.g., the number of telephone lines, the amount of electricity generating capacity, and the length of the road network. These measures are ‘standardized’, as follows:

1. If the indicator is not already normalized by a meaningful scaling factor, e.g., land area or total population, calculate an appropriate normalized value. This is based on the notion that, for example, it makes more sense to compare countries based on the number of telephones per person rather than the total number of telephones. The following figure shows the normalized indicators used for each of the component indices.
2. The logarithms of the normalized indicators are calculated.
3. The mean and standard deviation for each of the normalized and logged indicators in the year 2010 are calculated in the pre-processor. These are stored in the vectors INFRAINDTRANCOMPMEANI, INFRAINDTRANCOMPSDI, INFRAINDELECCOMPMEANI, INFRAINDELECCOMPSDI, INFRAINDWATSANCOMPMEANI, and INFRAINDWATSANCOMPSDI, each of which has an entry for each indicator included in the component index.
4. In each forecast year, a z-value for each of the normalized indicators is calculated by subtracting the mean value for the year 2010 and then dividing by the standard deviation for the year. This provides a more standardized measure of the difference across countries and is independent of the original units of measure. If a country has negative (positive) z-value for a particular indicator, this indicates that its level of that indicator is smaller (greater) than it was for the average country in 2010. By definition, the aggregated z-value for the world for each indicator in 2010 is equal to 0.
   

The component indices are then calculated as a weighted sum of the z-values for the normalized indicators used for each of the component indices. The weights are given by the parameters infraindtrancompwt , infraindeleccompwt , and infraindwatsancompwt , where, once again each of these is a vector with an entry for each indicator included in the component index. Finally, the overall traditional infrastructure index, INFRAINDTRAD, is calculated as a weighted sum of the component indices. The weights are given by the parameter infraindtradcompwt , which is a vector with three entries, one for each of the component indices.

As with the z-values for the individual indicators, a negative (positive) value of for one the component indices or the overall index implies that a country ranks below (above) the average country in 2010 for that indicator. Furthermore, by definition, the aggregated value for the world for each index in 2010 is equal to 0.

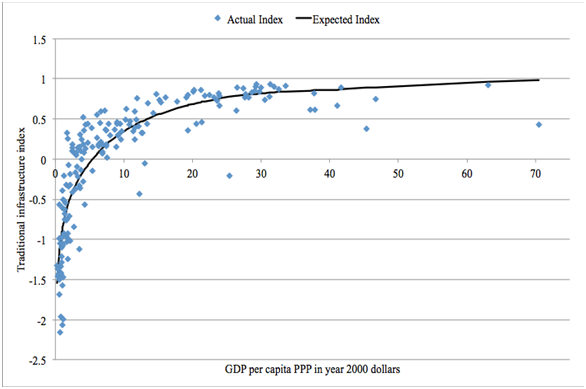
We use the overall Traditional Infrastructure Index to calculate the impact of traditional infrastructure on MFP in the same way as we do for most factors that influence MFP. As described by Hughes (2007: 15–16), we do this by comparing the value of INFRAINDTRAD to the value of INFRAINDTRADEXP, which is calculated using a benchmark function^[1]  that indicates what value we would expect to see for a country given its current level of GDP per capita (see the figure below). A country whose index falls above (below) the benchmark value receives a boost to (reduction from) its MFP. For example, Gabon and Latvia have similar levels of GDP per capita in 2010, but Latvia’s Traditional Infrastructure Index falls well above the benchmark line, while Gabon’s falls well below. Thus, the former will receive a boost to its MFP due to traditional infrastructure, while the latter will receive a reduction.

The size of the boost or reduction depends on the distance from the benchmark value, INFRAINDTRAD – INFRAINDTRADEXP, and a factor relating this distance to productivity, which is given by the parameter mfpinfrindtrad . Calderón and Servén (2010a: i35) presented a value of 2.193 as their estimate of the increase in annual average growth rate of GDP per capita for an increase in 1 unit of their index. Based on this, we use a default value of 2 for the effect of traditional infrastructure on MFP. Specifically, if the value of the Traditional Infrastructure Index for a country is a full point above its expected value in a given year, it would receive a 2 percentage point boost to its MFP, which roughly translates into the same increase in growth in GDP per capita, over the coming year. The model user can change this value, allowing for exploration of the sensitivity of model results to the traditional infrastructure parameter.

ICT

The ICT Index, INFRAINDICT ^[2] , is calculated as a weighted average of the subscription rates for three of the four different kinds of ICT – mobile phones, fixed broadband, and mobile broadband. Since the subscription rates for mobile phones and mobile broadband saturate at 150 per 100 persons, their values are first multiplied by 2/3 so that they range from 0 to 100. The weights are given by the parameter infraindictcompwt , which is a vector with three entries, one for each of the component indices. By default, these values are set to 1, indicating equal weighting.

When considering the impact of ICT infrastructure on MFP, using the same approach as for traditional infrastructure would be problematic. Our formulation for forecasting ICT infrastructure includes a technology shift factor. Therefore, any relationship between GDP per capita and the expected level of ICT would not remain stable over time; for example, a country with a GDP per capita of $5,000 in 2015 would be expected to have more ICT infrastructure than a country with a GDP per capita of $5,000 in 2010.

We therefore associate the growth contribution from ICT advances with annual changes in the ICT Index, rather than with the level of the index as we do for traditional infrastructure. We multiply the annual unit change in the ICT Index by the parameter mfpinfrindict . Qiang, Rossotto and Kimura (2009: 45) estimated that each 10 percent increase in broadband penetration in developing countries increased the growth rate of per capita GDP by 1.38 percentage points (by 1.21 percentage points for developed countries) during the 1980 to 2006 period. We arbitrarily reduced the impact by using a default value of 0.8 because our index is a mixture of several types of ICT infrastructures, not all of which might have as strong an impact on economic productivity as does broadband. Thus, a 10 point increase in the value of the ICT index would result in a 0.8 addition to MFP, or an approximate increase of 0.8 percent in GDP per capita.

There is one obviously questionable implication of this approach. When a country reaches saturation in the ICT Index, it will no longer receive a productivity boost from ICT. Given the current rapid increase in mobile telephones and mobile broadband that together make up two-thirds of the ICT Index, we see in most scenarios a near-term boost to MFP from ICT in much of the world, followed by little or no contribution later in the horizon. Our uncertainty with respect to appropriate treatment of the longer-term contribution of ICT points to one of the limitations of trying to forecast rapidly changing technologies.

Impacts on health

There are many ways in which infrastructure can affect human health. We have chosen to limit our inclusion of these effects to a small set, specifically the impact of (1) unsafe water, sanitation, and hygiene directly on diarrheal diseases, and indirectly on diseases related to undernutrition; and (2) indoor air pollution on respiratory infections, such as pneumonia, and respiratory diseases, such as chronic obstructive pulmonary disease. These health outcomes are influenced directly by infrastructure via our measures of access to improved sources of drinking water and sanitation and the use of solid fuels in the home. These measures serve as proxies for the environmental health risks linked to infrastructure in IFs. We explored these effects in a previous volume in this series, Improving Global Health (B.Hughes, Kuhn, et al. 2011: 95–100), and have some confidence in the reasonableness of our results.

Our approach for estimating the impact of these health risks is described in the health documentation. Therefore, we provide only a brief overview here. In general, we compare the forecasted values of these infrastructure indicators to values that we would anticipate based only on income and educational attainment (distal drivers). If the estimated and expected values differ, we adjust the levels of mortality and morbidity for the associated diseases forecasted based only on the distal drivers. For example, if the levels of access to improved sources of water and sanitation are higher than expected, we reduce the mortality rate from diarrheal diseases. The amount by which the mortality rate is reduced is based on the analysis presented in the Comparative Risk Analysis work of the World Health Organization (Ezzati et al. 2004). This general approach, comparing forecasted values with expected ones and translating the difference into impact in a forward linkage, is fundamentally similar to the method described above for linking infrastructure development and economic productivity.

---

[1] This benchmark function is actually the combination of two functions: 1) INFRAINDTRADEXP = -0.881 + 0.519 * GDPPCPPP at levels of GDPPCPPP below $5000 and 2) INFRAINDTRADEXP = 2.767 + 0.225 * GDPPCPPP at levels of GDPPCPPP above $40000, with blending between these two thresholds.

[2] A separate index, INFRAINDICTZ , is also calculated following the same approach as for the component indices of traditional infrastructure. This is only used for display purposes.

Infrastructure Equations

Overview

The primary equations in the infrastructure model in IFs are those for estimating the expected levels of infrastructure stocks or access. Each of the estimated equations relates one aspect of physical infrastructure to specific economic, structural, and demographic drivers; in some cases these equations also include other types of infrastructure, creating explicit linkages across those infrastructures. While a number of earlier studies did provide equations for forecasting future levels of some of the types of physical infrastructure we include, we chose to undertake our own analyses for the purposes of this volume. This allowed us to use more recent data to drive the relationships than earlier studies and to better integrate the resulting relationships within the broader IFs system.

Our choices of the driving variables ultimately included in the equations were influenced by theoretical considerations, previous efforts, the availability of data, and, of course, the analytical results themselves. These factors also influenced our choices of functional forms. In particular, for variables that have natural minimums and maximums, such as the percentage of population with access to electricity, we use functional forms that guarantee that the forecasted values fall in this range.

The basic equations shown below provide only the initial estimates of the expected levels of the specific infrastructure stock or access. The final values are adjusted based upon a number of algorithmic and scenario-specific processes, including the use of shift factors, multipliers, extrapolative formulations, targeting processes. Some key aspects of these algorithmic processes, including key parameters available to the user for scenario development, are provided below the definitions of the variables used in the basic equations. Finally, the nature of the data used for estimation, the model fitted, and the R-squared values for a fit of the predicted against the actual historical values used for our estimations are also provided.

As with the flow charts, this section presents the equations grouped by the four categories of infrastructure: transportation, electricity, water and sanitation, and ICT. Unless specified otherwise, in all of the following equations, the subscripts r and t refer to region/country and time/year, respectively. 

For help understanding the equations see Notation.

Equations: Transportation Infrastructure

The estimated equations for transportation infrastructure in IFs are: 1) the total road density in kilometers per 1000 hectares, INFRAROAD, 2) the percentage of roads that are paved, INFRAROADPAVEDPCNT, and 3) the Rural Access Index, INFRAROADRAI, the percentage of the rural population living within two kilometers of an all-season road. From these we can calculate other transportation indicators. 

Total road density

$ln(INFRAROAD_{r,t})=-2.539+0.483*ln({\frac {GDPP_{r,t}}{LANDAREA_{r,t}}})+0.183*ln({\frac {POP_{r,t}}{LANDAREA_{r,t}}}-0.102*ln(LANDAREA_{r,t})$

INFRAROAD = road network density in kilometers per 1,000 hectares

GDPP = gross domestic product at purchasing power parity in billion constant 2005 dollars

LANDAREA = land area in 10,000 square kilometers (million hectares)

POP = total population in million persons

• uses extrapolative formulation: extmafuncroad, extmaposnconvtimeroad, extmaposnroad
• additive shift factor: RoadDensShift, downward shift over 300 years, upward shift over 40 years
• multiplier: infraroadm
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• pooled cross-sectional data, OLS regression, R-squared = 0.79

Percentage of total roads that are paved

$INFRAROADPAVEDPCNT_{r,t}={\frac {100}{1+e^{-(-1.022+0.833*GDPPCP_{r,t}+0.756*POP_{r,t}-0.726*LANDAREA_{r,t}-0.267*INFRAROAD_{r,t}})}}$

INFRAROADPAVEDPCNT = road network, paved percent in percentage

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

LANDAREA = land area in 10,000 square kilometers (million square hectares)

POP = total population in million persons

INFRAROAD = road network density in kilometers per 1,000 hectares

• uses extrapolative formulation: extmafuncroadpaved, extmaposnconvtimeroadpaved, extmaposnroadpaved
• additive shift factor: INFRARoadPavedPcntShift, downward shift over 500 years, upward shift over 50 years
• multiplier: infraroadpavedpcntm
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• pooled cross-sectional data, OLS regression, R-squared = 0.45

Rural Access Index

$INFRAROADRAI_{r,t}=100*e^{-3.558+1.328*ln({\frac {GDPPC_{r,t}*1000}{LANDAREA_{r,t}}})+0.239*ln(INFRAROAD_{r,t}*{\frac {LANDAREA_{r,t}*1000}{POP_{r,t}}})}$

INFRAROADRAI = Rural Access Index, percent of rural population living within 2 kilometers of an all-weather road in percentage

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

LANDAREA = land area in 10,000 square kilometers (million square hectares)

POP = total population in million persons

INFRAROAD = road network density in kilometers per 1,000 hectares

• additive shift factor: INFRAROADRAIShift, downward shift over 500 years, upward shift over 50 years
• there is currently no multiplier for INFRAROADRAI
• targeting parameters: infraroadraitrgtval, infraroadraitrgtyr, infraroadraisetar, infraroadraiseyrtar
• value is not allowed to decline unless lack of finance for maintenance
• cross-sectional data, OLS regression, R-squared = 0.51

Equations: Energy Infrastructure

Percentage of urban population with access to electricity

$INFRAELECACC(urban)_{r,t}={\frac {100}{1+e^{-(1.144-4.858*{\frac {INCOMELT1CS_{r,t-1}}{POP_{r,t-1}}}+0.837*GOVEFFECT_{r,t})}}}$

INFRAELECACC(urban) = percent of urban population with access to electricity in percentage

INCOMELT1CS = population with income less than $1.25 per day, cross sectional computation in millions

POP = total population in million persons

GOVEFFECT = government effectiveness using the World Bank WGI scale, shifting it 2.5 points so that it runs from 0-5 instead of from -2.5 to 2.5

• additive shift factor: INFRAELECACCShift(R%, Urban), downward shift over 500 years, upward shift over 50 years
• multiplier: infraelecaccm
• targeting parameters: infraelecacctrgtval, infraelecacctrgtyr, infraelecaccsetar, infraelecaccseyrtar
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• cross-sectional data, GLM regression, R-squared = 0.68

Percentage of rural population with access to electricity

$INFRAELECACC(rural)_{r,t}={\frac {100}{1+e^{-(-0.500-6.925*{\frac {INCOMELT1CS_{r,t-1}}{POP_{r,t-1}}}+0.858*GOVEFFECT_{r,t})}}}$

INFRAELECACC(rural) = percent of urban population with access to electricity in percentage

INCOMELT1CS = population with income less than $1.25 per day, cross sectional computation in millions

POP = total population in million persons

GOVEFFECT = government effectiveness using the World Bank WGI scale, shifting it 2.5 points so that it runs from 0-5 instead of from -2.5 to 2.5

• shift factor: INFRAELECACCShift(R%, Urban), downward shift over 500 years, upward shift over 50 years
• multiplier: infraelecaccm
• targeting parameters: infraelecacctrgtval, infraelecacctrgtyr, infraelecaccsetar, infraelecaccseyrtar
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• cross-sectional data, GLM regression, R-squared = 0.77

Ratio of electricity use to total primary energy demand

$ENELECSHRENDEM_{r,t}=0.979*GDPPCP_{r,t}^{0.275}*INFRAELECACC(national)_{r,t}^{0.492}*FossilShare_{r,t=1}^{-0.077}*NonFossilShare_{r,t=1}^{0.123}$

where

$FossilShare_{r,t=1}={\frac {ENP(oil)_{r,t=1}+ENP(gas)_{r,t=1}+ENP(coal)_{r,t=1}}{ENDEMSH_{r,t=1}}}$

$NonFossilShare_{r,t=1}={\frac {ENP(hydro)_{r,t=1}+ENP(renew)_{r,t=1}}{ENDEMSH_{r,t=1}}}$

ENELECSHRENDEM = ratio of electricity use to total primary energy demand, in percentage

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

INFRAELECACC(national) = percent of total population with access to electricity in percentage

FossilShare = ratio of fossil fuel production to total primary energy demand in base year, as a fraction

NonFossilShare= ratio of hydroelectric and renewable energy production to total primary energy demand in base year, as a fraction

ENP = energy production for oil, gas, coal, hydro, and other renewables in billion barrels of oil equivalent

ENDEM = total primary energy use in billion barrels of oil equivalent

• uses an extrapolative formulation: extmafuncenelecshr, extmaposnconvtimeenelecshr, extmaposnenelecshr
• no shift factor
• multiplier: enelecshrendemm
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• cross-sectional data, OLS regression, R-squared = 0.65

As described in the flowchart for electricity the value of ENELECSHRENDEM is used to calculate the value of desired electricity use, given by INFRAELEC * POP, where INFRAELEC is electricity consumption per capita in kilowatt-hours and POP is total population in million persons. INFRAELEC is in initially calculated as:

$INFRAELEC_{r,t}=ENELECSHRENDEM_{r,t}*{\frac {ENDEM_{r,t}*EnDemDFRIVal_{r,t}*17,000}{POP_{r,t}}}$

INFRAELEC = electricity consumption per capita in kilowatt-hours

ENDEM = total primary energy use in billion barrels of oil equivalent

EnDemDFRI = a multiplicative shift factor based on the ratio of the actual energy consumption in physical units in the historical data to the apparent energy consumption calculated in the pre-processor as part of adjusting the physical data to match the financial data on energy imports and exports; this converges to a value of 1 over a number of years given by the parameter enconv

17,000 = the conversion factor from barrels of oil equivalent to kilowatt-hours

POP = total population in million persons

• an additional multiplicative shift factor, InfraElecRI, which converges over 40 years to a value of 1, is used to further adjust the estimate of INFRAELEC

Percentage of electricity lost in transmission and distribution

$INFRAELECTRANLOSS_{r,t}=e^{(3.125-0.026*GDPPCP_{r,t}-0.125*GOVREGQUAL_{r,t})}$

INFRAELECTRANLOSS = transmission and distribution loss as a percentage of total electricity production, in percentage

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

GOVEREGQUAL = government regulatory quality using the World Bank WGI scale, shifting it 2.5 points so that it runs from 0-5 instead of from -2.5 to 2.5

• uses extrapolative formulation: extmafuncelectran, extmaposnconvtimeelectran, extmaposnelectran
• additive shift factor: INFRAELECTRANLOSSShift, converges downward over 50 years, upward over 500 years
• multiplier: infraelectranlossm
• bound between 3 and 90
• 'pooled cross-sectional data, OLS regression, R-squared = 0.85 '

Percentage of population primarily using solid fuels for heating and cooking

$ENSOLFUEL_{r,t}={\frac {100}{1+e^{-(2.823+0.166*GDPPCP_{r,t}+0.032*INFRAELECACC(national)_{r,t})}}}$

ENSOLFUEL = ratio of electricity use to total primary energy demand, in percentage

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

INFRAELECACC(national) = percent of total population with access to electricity in percentage

• multiplicative shift factor: ENSOLFUELShift; never converges
• multiplier: ensolfuelm
• targeting parameters: ensolfuelsetar, ensolfueltrgtyr, ensolfuelsetar, ensolfuelseyrtar
• hold switch: ensolflhldsw, fixes value of ENSOLFUEL at initial year value
• cross-sectional data, GLM regression, R-squared = 0.8

Equations: Water and Sanitation Infrastructure

Percentage of population with access to improved drinking water and sanitation

For access to water and sanitation, we use a nominal logistic model to determine the share of the population in each category of access. For both water and sanitation, the number of categories is 3. For water these are no improved access, other improved access, and piped; for sanitation they are other unimproved access, shared access, and improved access.

The values p_i shown below represent the share of population with access to each of these categories. The resulting values of p_iwill all fall between 0 and 1 and sum to 1. These are then multiplied by100 in order to obtain values that range between 0 and 100 and sum to 100.

$P_{i}={\frac {S_{i}}{1+\sum _{i=1^{S_{i}}}^{2}}}$

for i = 1 to 2

and

$P_{3}=1-\sum _{i=1^{P_{i}}}^{2}$

where

$S_{i}=e^{(a_{i}+\sum _{j=1}^{n}b_{i,j}*x_{j})}$

for i = 1 to 2

n is the number of explanatory variables

Estimated coefficients
	Intercept	EDYRSAGE25 r,t	GDPPCP r,t	INCOMELT1CS r,t / POP r,t * 100	GDS(health) r,t / GDP r,t * 100
Water
s0	0.47200933	-0.4414453	-0.7033376	0.0253734	-0.1616335
s1	1.17414971	0.13867779	-1.1508133	0.01181508	-0.2769033
Sanitation
s0	0.73081107	-0.6420051	-0.4497351	0.02170283	-0.1562885
s1	-2.1593291	0.22539909	-0.3555466	0.02823687	-0.1579957

EDYEARSAGE25 = mean years of education for adults over the age of 25, in years

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

INCOMELT1CS = population with income less than $1.25 per day, cross sectional computation in millions

POP = total population in million persons

GDS(health) = government expenditure on health in billion constant 2005 dollars

GDP = gross domestic product at market exchange rates in billion constant 2005 dollars

• additive shift factors: WATSAFEshift and SANITATIONShift; converge over watsanconv years for high and low categories; for intermediate categories, convergence time is 20 years for positive shift factors and 50 years for negative shift factors
• multipliers; watsafem and sanitationm
• targeting parameters: sanitationtrgtval, sanitationtrgtyr, sanitnoconsetar, sanitnoconseyrtar, sanitimpconsetar, sanitnoconsetar, sanitnoconseyrtar, watsafetrgtval, watsafetrgtyr, watsafehhconsetar, watsafeimpconsetar, watsafenoconsetar, watsafenoconseyrtar,
• hold switches: watsafhldsw and sanithldsw, , fixes value of WATSAFE and SANITATION at initial year value
• values are normalized so that the three categories for water and sanitation each sum to 100
• pooled cross-sectional data, nominal logistic regression, R-squared = 0.85 for safe water, 0.87 for sanitation

Percentage of population with wastewater collection

$WATWASTE_{r,t}={\frac {SANITATION(improved)_{r,t}}{1+e^{-(-2.4+0.043*GDPPCP_{r,t}+0.042*{\frac {POPURBAN_{r,t}}{POP_{r,t}}})}}}$

WATWASTE = percent of population with wastewater collection, in percentage

SANITATION(improved) = percent of population with access to improved sanitation, in percentage

POPURBAN = urban population in million persons

POP = total population in million persons

• uses extrapolative formulation – coefficients are hard coded
• additive shift factor: WatWasteColShift; converge upward over 25 years, downward over 250 years
• multiplier: watwastem
• no targeting parameters
• value is not allowed to exceed SANITATION(improved)
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenanc
• pooled cross-sectional data, OLS regression with country random effect, R-squared = 0.34

Percentage of population with wastewater treatment

$WATWASTETREAT_{r,t}={\frac {100}{1+e^{-(-2.482+0.038*GDPPCP_{r,t}+0.029*WATWASTE_{r,t})}}}$

WATWASTETREAT = percent of population with wastewater treatment, in percentage

WATWASTE = percent of population with wastewater collection, in percentage

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

• additive shift factor: WatWasteTreatShift; converge upward over 25 years, downward over 250 years
• multiplier: watwastetreatm
• targeting parameters: watwastetreatsetar. watwastetreatseyrtar (no targeting parameters for absolute targets)
• value is not allowed to exceed WATWASTETREAT
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• pooled cross-sectional data, GLM regression, R-squared = 0.59

Equations: ICT Infrastructure

Fixed telephone lines per 100 persons

$INFRATELE_{r,t}=1.030+2.554*GDPPCP_{r,t}-0.033*GDPPCP_{r,t}^{2}$

INFRATELE = fixed telephone lines per 100 persons

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

• uses extrapolative formulation – parameters are hard coded
• no shift factor
• multiplier: infratelem
• no targeting parameters
• when ICTMOBIL reaches 30, if INFRATELE > 2.5 value will fall to level of 2.5 over time period given by infrateledtfp: if INFRATELE < 2.5, then can continue to grow
• cross-sectional data, OLS regression, R-squared = 0.70

 

Mobile telephone subscriptions per 100 persons

$ICTMOBIL_{r,t}=43.938+23.919*ln(GDPPCP_{r,t})+1.405*GOVREGQUAL_{r,t}$

ICTMOBIL = mobile phone subscriptions per 100 persons

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

GOVEREGQUAL = government regulatory quality using the World Bank WGI scale, shifting it 2.5 points so that it runs from 0-5 instead of from -2.5 to 2.5

• additive shift factor: MOBILshift; converge upward over 100 years, no convergence downward
• multiplier: ictmobilm
• targeting parameters: ictmobilsetar. ictmobilseyrtar (no targeting parameters for absolute targets)
• tech shift parameters: ictmobiltecinflection, ictmobiltechighrt, ictmobilteclowrt
• saturation level: ictmobilsaturation
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• cross-sectional data, OLS regression, R-squared = 0.53

 

Fixed broadband subscriptions per 100 persons

$ICTBROAD_{r,t}=-12.581+2.534*ln(GDPPCP_{r,t})+6.496*GOVREGQUAL_{r,t}$

ICTBROAD = fixed broadband subscriptions per 100 persons

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

GOVEREGQUAL = government regulatory quality using the World Bank WGI scale, shifting it 2.5 points so that it runs from 0-5 instead of from -2.5 to 2.5

• additive shift factor: BROADshift; converges over 100 years (both upwards and downwards)
• multiplier: ictbroadm
• targeting parameters: ictbroadsetar, ictbroadseyrtar (no targeting parameters for absolute targets)
• urbanization increases growth using parameters ictbroadurimpmin and ictbroadurimpmax
• as INFRATELE falls, this boosts growth of fixed broadband using the parameter ictbroadfromtelem
• tech shift parameters: ictbroadtecinflection, ictbroadtechighrt, ictbroadteclowrt
• saturation level: given by ictbroadcap (not in common block, currently hard coded as 50)
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• cross-sectional data, OLS regression, R-squared = 0.74

 

Mobile broadband subscriptions per 100 persons

$ICTBROADMOBIL_{r,t}=-21.827+9.139*ln(GDPPCP_{r,t})+9.357*GOVREGQUAL_{r,t}$

ICTBROADMOBIL = mobile broadband subscriptions per 100 persons

GDPPCP = gross domestic product per capita at purchasing power parity in thousand constant 2005 dollars

GOVEREGQUAL = government regulatory quality using the World Bank WGI scale, shifting it 2.5 points so that it runs from 0-5 instead of from -2.5 to 2.5

• additive shift factor: BroadMOBILshift; converge upward over 100 years, no convergence downward
• multiplier: ictbroadmobilm
• targeting parameters: ictbroadmobiltrgtval, ictbroadmobiltrgtyr, ictbroadmobilsetar, ictbroadmobilseyrtar
• tech shift parameters: ictbroadmobiltecinflection, ictbroadmobiltechighrt, ictbroadmobilteclowrt
• saturation level: ictmobilsaturation
• value is not allowed to exceed ICTMOBIL
• value is not allowed to decline in the absence of a target or multiplier or lack of finance for maintenance
• cross-sectional data, OLS regression, R-squared = 0.70