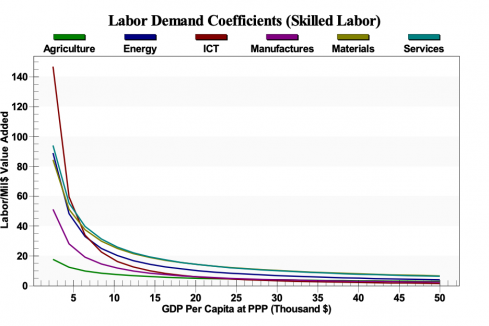
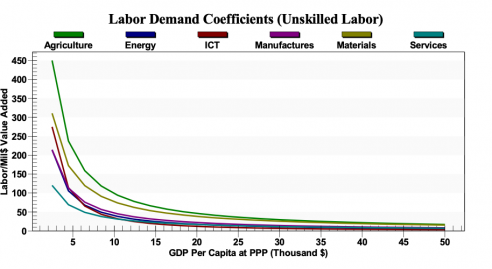
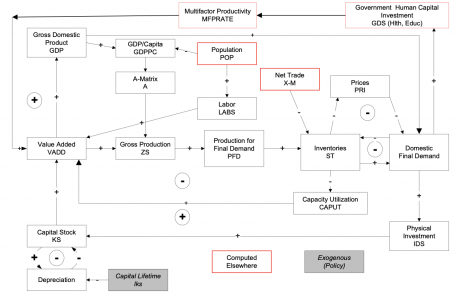
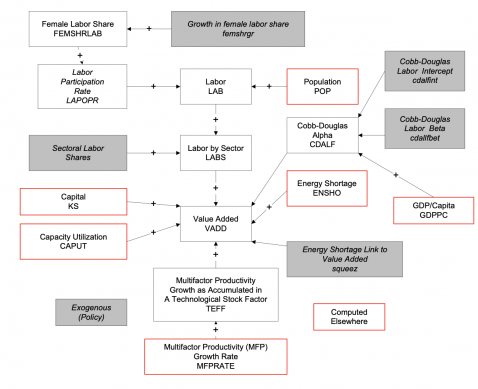
Economics
1 Introduction: Foundations
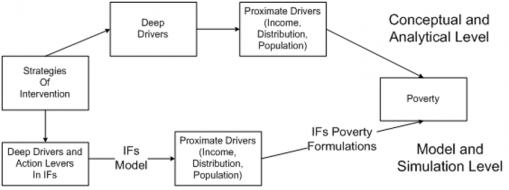
This section provides a brief introduction to the full IFs forecasting system before turning to an identification of three major and in combination unique features of IFs economic model: its production function, social accounting matrix, and equilibration dynamics. Subsequent sections will elaborate those elements of the economic model before documenting some additional aspects of that model, including its bilateral elaboration of trade and other international flows, its labor market, and its representation of the informal economy. Two additional sections address its representations of inequality and poverty. Supplemental appendices provide additional information about data foundations and present some block diagrams of the model.
1.1 The Broader IFS Context of the Economic Model
Since well before the promulgation of Sustainable Development Goals (SDGs), the philosophy underlying the IFs project has been that multiple global issues benefit greatly from integrated analysis and action. Such issues, as in the SDGs, cut across the general categories of (1) human development (demography, health, education, and basic income levels), (2) social organization and development (socio-political stability, equity and governance with economic advance), and (3) sustainable development (protection of the environment against climate change and other damage). Figure 1.1 roughly maps the models of the IFs system to the SDGs organized in the three issue sets. IFs includes multiple hard-linked models, including demographic, education, health, economic, infrastructure, governance, international politics, agriculture, energy, and environment sub-systems. Across its integrated components IFs can generate alternative scenario forecasts for 188 countries through 2100, including the Base Case scenario.
International Futures (IFs) falls generally into the categories of “world models” (Hughes 1985) and “integrated assessment models (IAMs)”. Its uniqueness lies partly in the extent of its issue coverage, allowing a large range of basic research opportunities and applied policy analysis. The software system has an easy-to-use interface. Also it is publicly and freely available on-line (at https://www.ifs.du.edu/ifs/frm_MainMenu.aspx). See also information on the Pardee Center at https://korbel.du.edu/pardee
Across time there have been numerous descriptions of the entire IFs system (Hughes 1999, 2001, 2016, and 2019: Hughes and Hillebrand 2006). Those, especially Hughes (2019), put it in the context of other world models and integrated assessment models. Briefly surveying in this subsection the models of IFs and some of their interconnections with each other and the economic model sets the stage for more extended explanation of the economic model. Because variables in the other models drive and/or are driven by the economic model, understanding those connections helps understand it.
Figure 1.1 The models of the International Futures (IFs) system and related SDGs. Source: Hughes, Hanna, et al. (2021).
The human development models facilitate the use of IFs in long-term economic forecasting. For instance, consistent with single-year time steps in the economy’s recursive structure, the structure of the demographic model is cohort-component and sex-specific with single-year cohorts that advance over time as the economic model does. The health model provides mortality calculations in 15 subcategories across communicable, non-communicable and injuries categories (Hughes, Kuhn, Peterson, Rothman and Solórzano 2011; Hughes, Kuhn, Peterson, Rothman, Solórzano, and Mathers 2011; Hughes et al., 2015; Kuhn, et al. 2016), using data from the Global Burden of Disease project. Fertility calculations draw upon infant mortality from the health model and on years of adult educational attainment from the education model (Dickson, Hughes, and Irfan 2010). The demographic model also forecasts migration patterns (Cantore and Cali 2015), which affect remittances in the economic model.
The education model also has cohort-component and sex-specific representation. Single-year cohorts of individuals progress through primary, lower secondary, upper secondary, and tertiary education. Very important to the economic model, they also carry years of formal education through adult years of working life. Together, the demographic model provides potential labor supply numbers to the economic model, while the health and education models provide variables that help determine economic productivity. Together with the demographic, health, and education models, the economic model and its attention to national and global income distribution (Hillebrand 2008) have been used to study prospects for reducing poverty and making progress toward other SDGs (Hughes and Irfan 2007; Hughes, et al. 2008; Milante, Hughes and Burt 2016; Moyer and Bohl, 2019; Hughes et al. 2020; Moyer and Hedden 2020; and Moyer et al. 2022).
The partial equilibrium agriculture model represents crop, meat, and fish categories. The energy model (Hughes 1986) has six categories of renewable and nonrenewable energy. Those two models are tightly integrated with the general equilibrium economic model, providing information on supply and demand for the first two of its six economic sectors. In turn, the general model provides investment allocations to the agriculture and energy models. In addition, the partial equilibrium models have a large role in calculations of variables within the environmental model that affect economic growth, including atmospheric carbon level (Hughes et al., 2011; Birkman et al 2012.
The socio-economic models are closely interlinked with each other and with models at the human development and sustainability levels of Figure 1.1. Governance, including levels of stability and instability (Hughes, et al., 2014; Joshi, Hughes, and Sisk 2015; Bowlsby et al. 2019) affects economic growth. Government finance affects health and education variables that also affect economic growth. That finance also has a key role within infrastructure (Rothman et al., 2013), the model for which represents the changing stock of transportation, electricity, water and sanitation, and information/communication technology infrastructures. That infrastructure again affects economic productivity. International relations help shape international flows of foreign assistance and remittances; in interaction with trade (Hillebrand 2010) they shape current account and international debt/asset balances, important economic variables. Future economic growth and broad global transitions (Hughes 1997; Gordon et al. 2011) depend also on technological advance; IFs has increasingly developed technology representatons (Hughes and Johnston 2005; Moyer and Hughes 2012; Hughes et al. 2017; Scott et al. 2022).
Long-term economic growth models differ on many dimensions. While some models rely primarily on statistical estimation of growth patterns from historical data, others build somewhat more heavily on elaborated representation of structural drivers of growth. For instance, the Bayesian latent factor model used by Muller Stock, and Watson (2022) is highly statistical; it was fitted to global GDP per capita data back to 1900. In contrast, and somewhat more like IFs, the economic models that have been used to generate the economic forecasts for the five Shared Socioeconomic Pathways have had more structural representation. For instance, they include production functions representing variables such as educational attainment and trade openness; see Crespo Cuaresma (2017) and Dellink Chateau, Lanzi and Magné (2017).
This sketch of the broader IFs system has laid foundations for focused elaboration of the economic model, beginning with a general survey of it.
1.2 The Economic Model
The International Futures (IFs) system’s economic representation is a global, annually recursive dynamic general equilibrium model, integrated extensively with all other models of IFs.
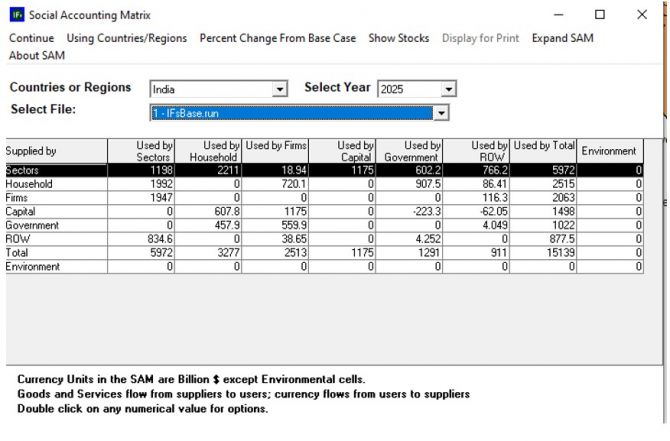
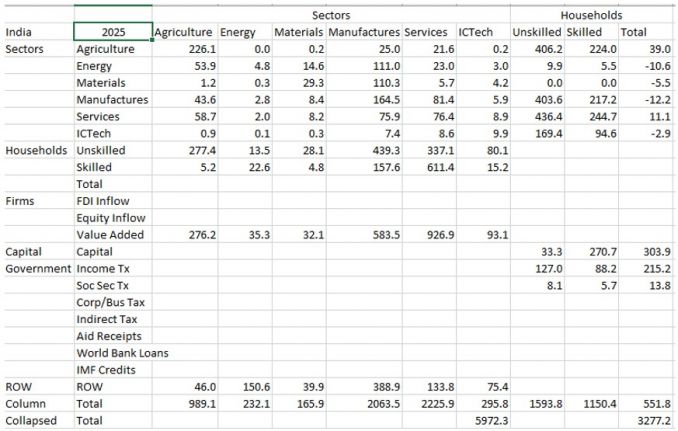
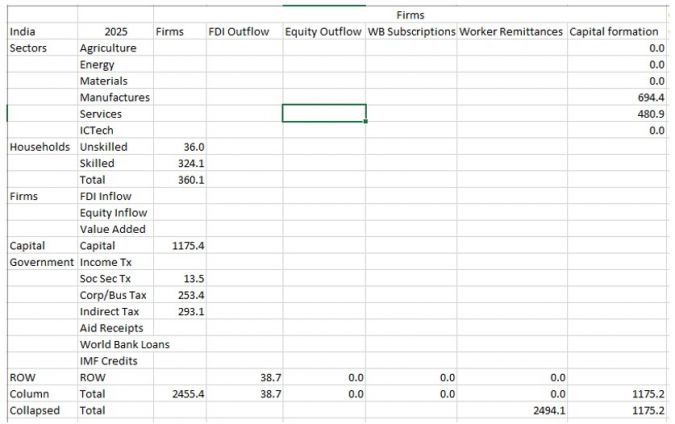
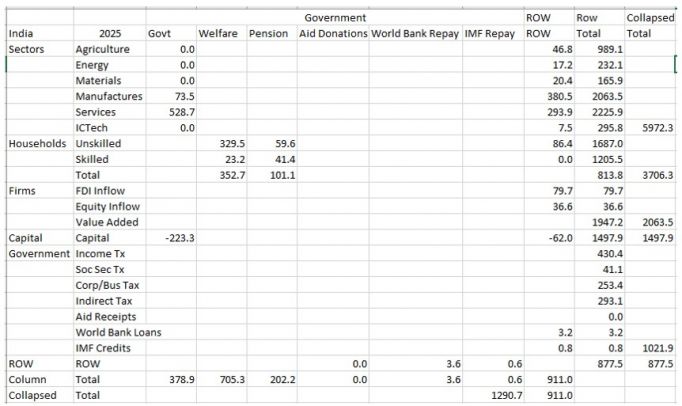
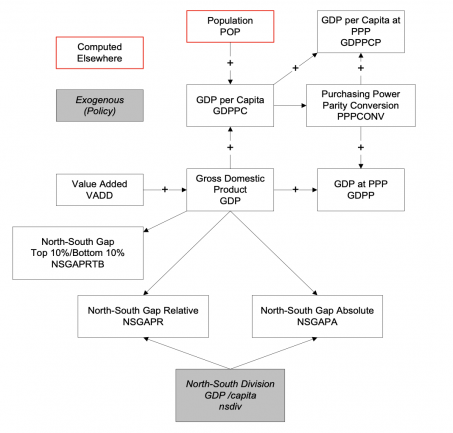
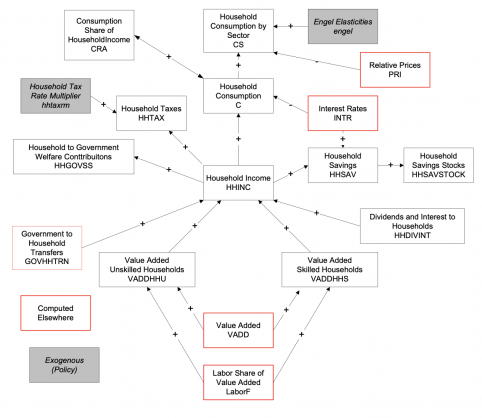
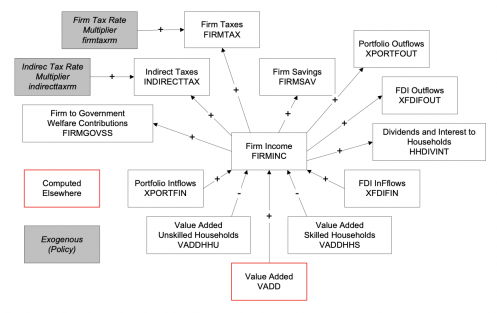
It draws on two general economic modeling traditions.[1] The first is the dynamic growth model of classical economics. In that tradition production functions play a central role. Consistent with that, within IFs the growth rates of labor force, capital stock, and multifactor productivity largely determine the overall magnitude of production and therefore of the economy. The second tradition is the general equilibrium model of neo-classical economics. The modeling of general equilibrium often involves a representation of social accounting matrices (SAMs). SAM-based models typically represent alternative equilibrium states for financial flows among actor categories via either comparative static analyses or as change across time in response to selected drivers. IFs contains a six-sector (agriculture, raw materials, energy, manufactures, services, and ICT) equilibrium-seeking representation of domestic supply, domestic demand, and trade. The goods and services market representation is embedded in a larger social accounting matrix structure that introduces the behavior of household, firm, and government agent classes and the financial flows they determine.
Three significant features differentiate IFs from most other models with these characteristics (Hughes 2019). First, the representation in IFs of economic growth is responsive to an unusually extensive set of productivity drivers, as well as to capital and labor. It is quite common in production functions to endogenize response of labor productivity or total factor productivity to education, R&D expenditures, and trade openness. Typically, modifiers of conditional convergence processes across countries represent such responsiveness (e.g. Crespo Cuaresma 2017; Dellink et al. 2017). IFs adds to these variables multiple other drivers including health, governance quality, infrastructure, and climate change (Hughes and Narayan 2021). This feature facilitates representing positive feedback loops or synergies across the broader IFs model system; for instance, expenditures on water and sanitation infrastructure can increase economic growth and, in turn, enhance capacity for additional investments in watsan or elsewhere.
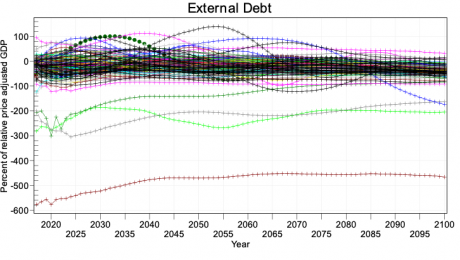
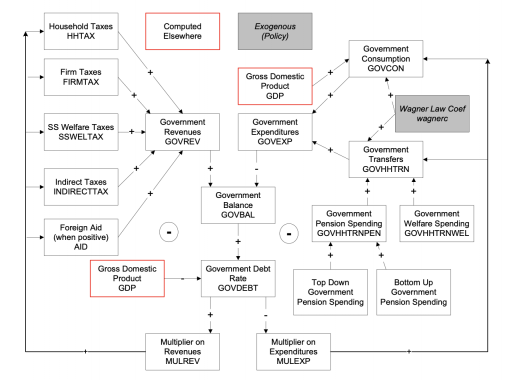
Second, the social accounting system of IFs has an especially extensive representation of government revenues and expenditures. One reason for this is that expenditures on education, health, and infrastructure (in addition to those on the military and R&D) hard link the IFs economic model to other large-scale IFs models in those issue areas. Because many policy analyses involve such expenditures, their representation facilitates tying developmental advance to spending, including also accounting for trade-offs and negative feedbacks. In support of initializing multiple streams of government revenue and expenditures (including transfer payments), IFs draws heavily on data from the International Monetary Fund, the World Bank, and the OECD. Hughes, et al. (2020) describe the complexity of the “nowcasting” within IFs that assures internal consistency of monetary and other data in the system’s base year, a capability that uses an integrated data preprocessor that can quickly process data updates across all models in IFs. Social accounting in IFs also has an extensive representation of international flows, augmenting trade with foreign aid and migration with associated remittances.
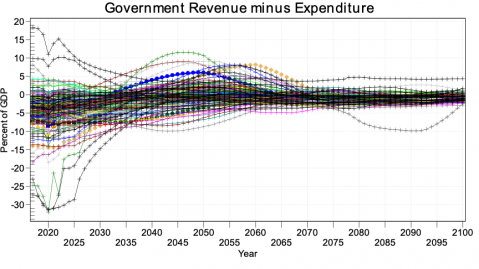
A third unusual feature of IFs is its representation of economies as chasing equilibrium across time rather than achieving it each year―while maintaining accounting consistency. Hence, for instance, IFs uses annual rise and fall in inventory stocks to generate price signals to the supply and demand sides of markets (domestically and internationally), and it uses net government debt and asset stocks to provide signals for changes in expenditures and revenues across time. Whereas SAMs focus on annual flows, this approach more generally underlays that flow matrix in IFs with a second and supportive matrix representation of financial stocks. This representation avoids the necessity of specifying closure rules in each time step for the equilibrations and facilitations scenario analysis with interventions on both demand and supply sides of agent behavior.
Several additional features are important within and because of the broader IFs system linking the economic model to other models within IFs. For instance, separate partial equilibrium models of agriculture and energy in physical terms produce values of production and trade that, when converted to currency, override the respective computations in the multi-sector economic model, while the accounting across sectors in that model provides realistic tradeoffs that constrain investment and shape the availability of it in the physical models. Also, a representation of the size of the informal economy across time allows calculation of its changing impacts on productivity and government revenues. Further, feedback of global warming to GDP and productivity builds on the approaches of Nordhaus and Moffat (2017) and Dietz and Stern (2015).
The structure of IFs also recognizes that short-term dynamics of economic growth differ from long-term dynamics. For instance, COVID-19 has disrupted economic growth and there is still uncertainty concerning (1) the degree to which the disruption is a relatively short-term fall in capacity utilization that will rebound post-pandemic and (2) how much of the growth loss represents factors such as reduced investment or obsolescence of capital stock and changing labor participation that will persist long after its end. Parameterization in IFs facilitates alternative scenarios.
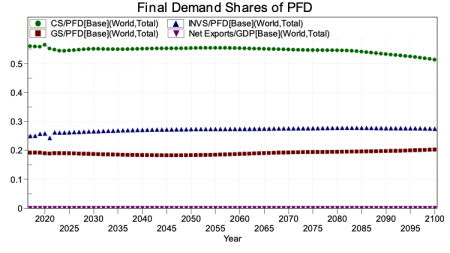
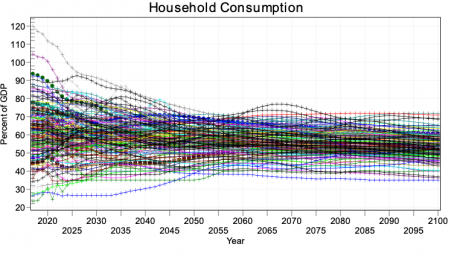
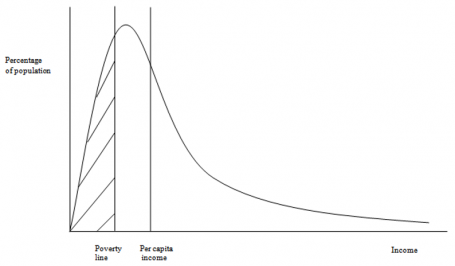
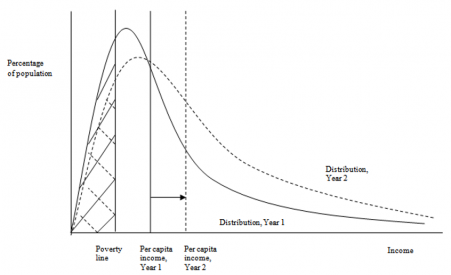
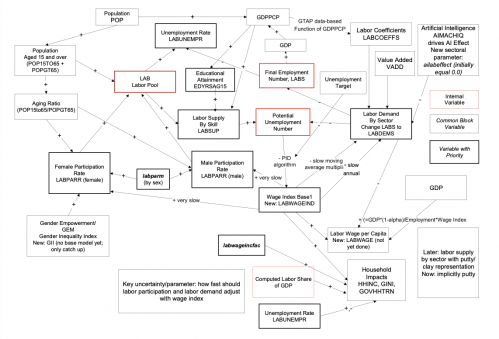
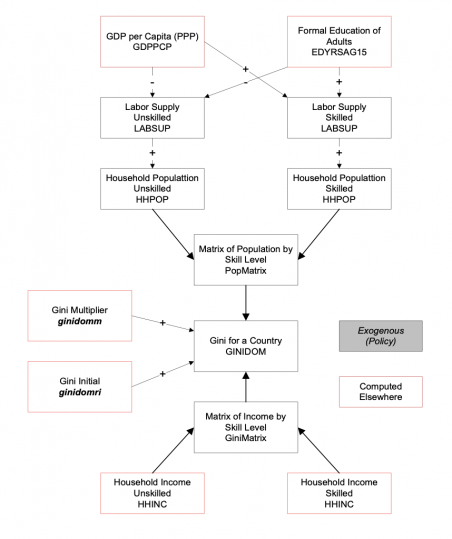
Also very important for the analysis done with the IFs system, including across the Sustainable Development Goals, the representation of household consumption in the SAM, in combination with the IFs educational model’s projections of the skill levels of those households, facilitates endogenized computation of changing income distributions. Average consumption and distribution provide the proximate foundations for forecasting of poverty in IFs, while the broader model represents their distal drivers. In general, the structures and usage of IFs have devoted a great deal of attention to such representations of human development, as well as to socioeconomic change and sustainability. Representation of both the labor market and the informal economy also support that attention.
Further, the inclusion with the IFs system of a “data preprocessor” supports continuous updating of a very large data base and automated recalculation of initial conditions and many parameters. The system’s user-friendly interface and open-source status have long contributed to widespread use, feedback, and enhancement. This documentation of the economic model “nexus” of IFs ranges across all these features of the system.
[1] Fardoust and Dhareshwar (2013) provide a useful review of past long-term economic forecasting efforts particularly within the World Bank, their successes and failures, and factors to consider in efforts going forward.
2 Goods and Services Market Supply Side and Economic Growth
Before turning to economic demand and financial flows within the social accounting matrix (SAM) and then moving to explanation of intertemporal dynamics, this section treats the supply side of the economic model.
2.1 Introduction
The goods and services market sits within the larger social accounting matrix that tracks financial flows among households, firms, and the government and that shapes the demand side of the market. The economic growth portion of the goods and services module responds to endogenous labor supply growth (from the demographic model with attention to participation rates, especially of women), endogenous capital stock growth (with a variety of investment level influences), and a mixture of endogenous and exogenous specification of advance in drivers of multifactor or total factor productivity (terms used interchangeably here). The productivity formulation represents a combination of generalized convergence and country-specific elements that together create a conditional convergence formulation.
Two "physical" or "commodity" models in IFs, agriculture and energy, have structures very similar to each other and to the economic model. Their partial equilibrium structures optionally, and by default in the Base Case and almost all other scenarios, drive supply and demand calculations of those sectors within the goods and services market module.
2.2 The Production Function: Overview
The core Cobb-Douglas equation for the production function computes value added (VADD) in each economic sector from sector-specific values of total factor (or multifactor) productivity (TEFF), capital (KS), labor (LABS), and capacity utilization (CAPUT), initially set exogenously (caputtar) and changed over time dynamically in response to inventory stock levels (see Section 4). A time-constant scaling factor (CDA) assures that value added is consistent with data the first year. The function requires sectoral exponents for capital (AlphaS) and labor that, assuming constant returns to scale, sum to one within sectors. Within IFs, gross domestic product (GDP) is the sum across sectors of valued added. Although the production function for VADD can serve all sectors of IFs, the parameters agon and enon act as switches. When their values are one, which is the default, production in the agricultural and primary energy sectors, respectively, are determined in the larger, partial equilibrium models and the values then override the computation of gross sectoral production (ZS). See this documentation (Section 3.3.1.2 within the SAM description) for explanation of how gross production from those models is used in association with intersectoral flows to compute value added for those sectors.
2.2.1 IFs Documentation Notation
IFs variable names accessible in the interface appear in upper case italics, while parameter names appear in bolded and italicized lower case. Variable names that appear in mixed case reflect other calculations local to the model code. The local variable names shown in documentation equations may differ somewhat from those in the code for clarity of presentation.
Subscripts:
- r is country/region (regions can be groups of countries or subregions within them)
- c is age category/cohort
- d is cause of death
- e is energy type
- f is food type
- g is government spending sector
- h is household type by skill level
- i is infrastructure category
- l is land category
- p is sex
- s is economic sector
- sk is skill level of labor
- wd is water demand sector
- ws is water supply sector
- t is time, and will not generally be shown unless the equation involves more than one time-step, e.g. with a lag from the preceding year (t-1), or referring to initial conditions (t=1)
2.3 The Production Function Continued
A later subsection of this documentation explains the drivers of investment and capital formation (net of depreciation). Investment is endogenously computed as part of the social accounting matrix structure and within the model’s equilibration system. A subsequent section elaborates the labor model of IFs with its attention to demographic structure and age-sex work-force participation rates.
The focus here will be on the multifactor (total factor) productivity term. That term is especially important in IFs because it is responsive to the dynamics of most of the other models in IFs, including those representing education, health, infrastructure, and governance. Solow (1956) long ago recognized that the standard Cobb-Douglas production function with a constant scaling coefficient in front of the capital and labor terms was inadequate because the expansion of capital stock and labor supply leave a large portion of economic growth unexplained. It then became standard practice to represent an exogenously specified growth of technology term in front of the capital and labor terms as "disembodied" technological progress (Allen 1968: Chapter 13). Romer (1994) began to show the value of unpacking such a term and specifying its elements in the model, thereby endogenously representing this otherwise very large residual, which we can understand to represent the growth of multifactor productivity (MFP).
In IFs that total endogenous productivity growth factor (TEFF) is the accumulation over time (hence a stock like labor and capital) of annual values of growth in multifactor productivity (MFPGROWTH).
There are many components contributing to growth of productivity, and there is a vast literature around them. See, for example, Barro and Sala-i-Martin (1999) for theoretical and empirical treatment of productivity drivers; also see Barro (1997) for empirical analysis (or McMahon 1999) for a focus on education
In the development of IFs there was a fundamental philosophic choice to make. One option was to keep the multi-factor productivity function very simple, perhaps to restrict it to one or two key drivers, and to estimate the function as carefully as possible. Suggestions from other modeling efforts include focusing on the advance of education, the extent of global connections of a national economy, the availability/price of energy, and the growth in electronic networking and the knowledge society.
The second option was to develop a function that included many more factors known or strongly suspected to influence productivity and to produce a more integrated representation of the function, using empirical research by others and within the project to aid the effort as much as possible. The advantages of the second approach include creating a model that is much more responsive to a wide range of policy levers over the long term. The disadvantages include inevitable complications with respect to overlap and redundancy of factor representation, as well as some considerable complexity of presentation. Because IFs is a thinking tool and an extensively integrated multi-model system, the second approach was adopted, and the production function has become an element of the economic model that will be subject to regular revision and enhancement. See Hughes and Narayan (2021) for an elaboration of the IFs approach as documented here, including explanation of parameterization of driver contributions.
The decision to represent so many productivity influencing variables led to another difference between IFs and many other economic models. Most often the representation of education, for example, is as a multiplier of labor in the production function. Rather than embed each of the multiple productivity drivers of IFs with only either capital or labor (and many, like infrastructure, clearly affect both), all contributions to productivity are represented within a dynamic elaboration of the Solow residual, i.e. as disembodied technological progress.
Stylistically (not using variables names in IFs code), there are four determinants of the growth of multifactor (or total factor) productivity, as indicated below and elaborated in following sub-sections.
The first two contributions represent the conditional convergence process at the core of TFP growth (Abramowitz 1986 and Baumol 1986 provided foundations for the theory of convergence). The first of those two (the Convergence Base Terms) is commonly represented in long-term economic models (e.g., Cuaresma 2017; Dellink et al. 2017) and itself has two components in IFs: (1) the technological progress of systemic leadership or mfpleadr (that role is assigned to the United States, although one can imagine it shifting to China or elsewhere over time; the parameter could be used in scenario analysis in many ways, even including the replication of Kondratieff or “long” waves) and (2) a catch-up technology premium term (MFPPREMIUM) specific to countries and typically related to their GDP per capita as a proxy for ability to adopt and adapt technology (see Johnson and Papageorgiou (2020) for analysis of convergence including its temporal intermittency and variation across country clubs).
The second general contribution driving growth in multifactor productivity (Conditional Convergence Modifications) is quite different in IFs than in other long-term economic models, at least with respect to its extensive elaboration. Specifically, it is the sum of four component elements that can accelerate or slow the conditional convergence process for each country. Those four components, each related to multiple variables in IFs and elaborated in subsequent discussion, represent the degree to which each country’s development of human (MFPHC), social (MFPSC), physical (MFPPC), and knowledge (MFPKN) capital, respectively, are above or below the level of development typically associated with the country’s GDP per capita. If above typical values, convergence is accelerated, and if below, convergence is retarded.
The third contribution driving productivity (Correction Factors) includes two correction terms, one specific to countries (MFPCORS) and one global (MFPGloCor). These can also be thought of as fixed effects terms that represent differences between model-based calculations of productivity growth in the base year and empirical analysis of that growth.
The final contribution contains three parameters that facilitate exogenous control of change in MFPGROWTH for scenario analysis (mfpbasgr, mfpbasinc, and mfpadd). Again, subsequent sub-sections will provide explanation.
In understanding the drivers of economic growth within and across countries and in structuring the IFs representations of productivity and growth, it is essential to have data and measurement of historical productivity and GDP growth patterns. The IFs system includes TFP data series from both the Penn World Tables (Feenstra, Inklaar,and Timmer 2015), also looking to the Conference Board (Erumban and de Vries 2016), which have been used in building the IFs formulation and in historical analysis of it.
Especially for the computation of the correction factors, but also for analysis of some of the other productivity driving factors to be explained below, it is necessary to have an estimate of the basic or core economic growth rate of the country, one that is not influenced by shorter-term events such as cyclical recessions or a pandemic like COVID. The computation of that core growth rate is done in two steps.
First, using historical GDP data the data preprocessor computes a long-term growth rate for each country (igdpr) that, while labeled an initial GDP growth rate, is a propensity for country-specific growth. Having it is important to initialization of the production function and MFP growth formulation, including the conditional convergence representation and the computation of correction factors. Note that igdpr is identified as a parameter in the use of IFs, allowing users to change the computed value easily for scenario analysis. The calculation of igdpr looks to the most recent 20 years of data and near-term future estimates of economic growth (from the IMF), computing average rates of growth in the earliest 15 of those and the latest 5 of those and then computing an average of the two values, weighting them equally and thereby giving more importance to more recent years. It was decided to exclude the years 2020-21 from this computation because COVID’s impact on growth in those years is not representative of the long-term growth patterns and the prospective advance of productivity. One great advantage of having the computation in the preprocessor is that rebasing of the IFs system automatically will continue to update the value of igdpr across time.
Second, even when quite a long historical period is used (with a length that considerably exceeds short-term business cycles and across a 20-year period that is sometimes felt to represent a real-estate-based cycle), countries can experience even quite long periods when GDP growth is greatly disrupted for reasons that we can reasonably expect not to continue. The pattern in Venezuela since the 1999 election of Hugo Chávez is an example. It is very improbable that the long-term growth potential of any country is less that the growth of population; it is possibly a bit more. Therefore, IFs calculates a corrected value of igdpr (igdprcor) that is set at the maximum of igdpr and the population growth rate (POPR) of the country in the base year plus a parameter for the minimum per capita rate assumed to be applicable (minpcgr). In default the value of that parameter is 0.0, but it allows flexibility in scenario analysis.
The following subsections will elaborate each of the four terms in the function that computes productivity growth.
2.4 The Core Representation of Productivity Convergence
As indicated, the Convergence Base Terms consist of two elements, a rate of technological advance at the system’s leading edge (mfpleadr) and a premium percentage productivity growth rate relative to the leader, MFPPREMIUM, which can be negative for some countries. (The rate in the leader's ICT sector gradually convergences over time to that of the service sector.)
PremTechComp is the name of a function in IFs, driven by the GDP per capita at purchasing power parity (GDPPCP). It computes the technology premium for all countries relative to the annual growth contribution that mfpleadr makes for the leader.
Representation of the function that links GDP per capita to the extent of convergence and divergence relative to the system leader is challenging in part because of the debates that have characterized the literature as to whether the global system’s pattern has been one of divergence or convergence. Pritchett (1997) in writing about “Divergence, Big Time” across well over a century reinforced the argument of many political economists of the time that convergence was very much not the dominant pattern. Even much more recently Johnson and Papageorgiou (2020) argued much the same. In contrast, Hughes and Narajan (2021) traced the shift of global patterns from divergence to convergence near the beginning of the new century and others have also found that shift to be very strong (Patel, Sandefur, and Subramanian 2021). Moreover, contrary to the notion of an invariant or very frequent middle-income trap, these studies suggest more commonly an inverted-U pattern of change in the convergence premium.
Given both the debate within the literature and the relative recency of the seeming global shift from divergence to convergence, the IFs system, which once hard-coded an inverted-U pattern of convergence, has been changed to structure endogenously in the model base year the PremTechComp function using data on world-wide patterns of economic growth in recent years. In the first model year the endogenous calculation of MFPPREMIUM uses igdprcor, mfpleadr, and calculations of labor and capital growth in the production function to compute average values (WBGroupCorrect) for the productivity growth increment in the function above relative to that of the leader within each of the four World Bank country income groupings (low, lower-middle, upper-middle, and high).
The average values of GDP per capita at PPP for each of the World Bank groupings (WBGroupGDPPCP) are also computed in the base year from that pattern in data of recent years. These averages of GDPPCP and computed technological growth premium relative to the system leader are four points that, with interpolation between them, create a conditional convergence function. When the base year for IFs was 2015 and 2017, those values did strongly suggest the inverted-U pattern of convergence across country-specific GDPPCP that began to prevail after about 2000 (the values of the points are visible to model users in techconv). As the model is rebased in future years, however, that pattern may change again. One last specification of importance in using the algorithm for future years is that countries with GDPPCP above that of the leader are assumed in function PremTechComp to have progressively higher negative values of convergence premium. Some, like countries heavily dependent on oil exports are unlikely in the long run to maintain their premium.
2.5 Accelerating and Slowing Conditional Convergence
Given the basic or core representation of conditional convergence as a function of the technological advance of the system leader and the pattern of convergence (or divergence) across other countries, all other terms in the computation of MFP growth across time (MFPGROWTH) are additions or subtractions relative to that core representation. Some of those terms, to be discussed later, are correction factors related to historical growth patterns or exogenous intervention points for scenario analysis. By far the most important increments or decrements are those identified earlier as Conditional Convergence Modifications.
As indicated earlier, those modifications are grouped into four clusters of variables across many of the other models in the IFs system; the clusters are identified as human capital, (MFPHC), social capital (MFPSC), physical capital (MFPPC), and knowledge capital (MFPKN).
The general logic relating each cluster of variables to the growth of multifactor productivity is the same. Each cluster aggregates several variables that generally contribute to productivity. For each variable, such as average years of adult education in the human capital cluster, there is an expected value and an actual value. It is the difference between actual and expected values that gives rise to a quantitively specific positive or negative contribution to productivity and growth.
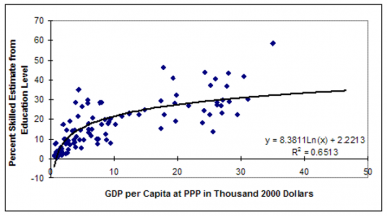
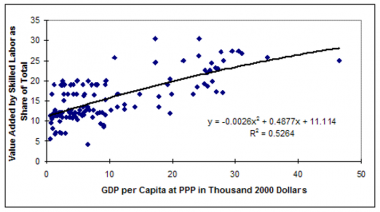
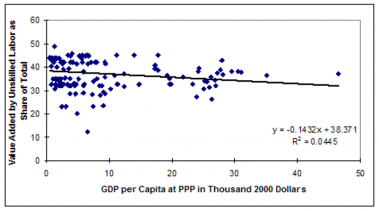
Most expected values are identified in a relationship with GDP per capita at PPP. That is, there is a tendency for most developmentally supportive variables to advance in a rough relationship of structural development with each other and with GDP per capita (Kuznets 1959 and 1966; Chenery and Syrquin 1975; Syrquin and Chenery 1989; Sachs 2005). To the degree that they do, such advance can be understood to be consistent also with the overall technological advance of the country. If, however, a variable such as years of formal education attained by adults exceeds the typical or expected value for a country at a given level of GDP per capita, we can expect that variable to add something more to productivity. Similarly, falling behind the expected value could retard productivity advance. To illustrate and emphasize this point, even a country for which adult education levels advance could find that education is not keeping up with the advance in other developmental variables including GDP per capita and find that its education levels move from contributing to productivity enhancement to decrementing that productivity enhancement.
2.5.1 Driver Cluster 1: Human Capital
In the human capital cluster there are six variables that add to or subtract from the human capital (MFPHC) term: the educational spending contribution (EdExpContrib), the years of adult education contribution (EdYrsContrib), the quality of adult educational attainment contribution (EdQualContrib), the boost from life expectancy years (LifExpEdYrsBoost) assumed to generate (via mfpedlifexp) extra years of education, the stunting contribution (StuntContrib) related to undernutrition of children, the disability contribution (DisabContrib) related to morbidity from the health model, and vocational education contribution (edVoccontrib) resulting from growth (or decline) in vocational share of lower and upper secondary enrollment,. The first six of these seven drivers have a similar formulation while the formulation for vocational education is slightly different. The first six, as computed often from extended formulations and even other models of the IFs system (as with life expectancy, computed in the health model) are compared with an expected value. In the case of disability, the expected value is set to the world average level (WorldDisAvg), but all other expected values (EdExpComp, EdYrsComp, EdQualComp, LifExpComp, and StuntingComp) are computed as functions of GDP per capita at PPP. As the provision of vocational education does not follow any common pattern or trend and is rather a matter of policy choices made (or will be made) by the particular country, it was not possible to calculate an expected value for this variable. We have instead computed the vocational education contribution from changes in vocational share over time with appropriate moving averages to capture the lag required in materializing such contribution and to smooth out the contribution over time. (Note: In the base case of the model, vocational shares do not change and as such EdVocContrib is zero).
In each case a parameter drawn from study of the literature and/or our own analysis converts the difference between actual and expected into a positive or negative contribution to MFP. (Because of the recursive structure of IFs, some terms rely on variables from the previous time step, estimated from the current time step with the parameter representing corrected core GDP growth, namely igdprcor.)
2.5.2 Driver Cluster 2: Social Capital
The logic of comparison of actual with expected values of six social capital drivers of productivity is the same as that described above for human capital. The six are economic freedom as in the Fraser Institute measure (EconFreeContrib), government effectiveness as in the World Bank measure (GovtEffContrib), corruption as in the Transparency International measure (CorruptContrib), democracy as in the Polity project measure (DemocPolicyContrib), freedom as in the Freedom House measure (FreedomContrib), and conflict as in the IFs project's own measure tied in turn to the work of the Political Instability Task Force (ConflictContrib). In each case other than that for conflict, the expected values (EconFreeComp, GovEffectComp, CorruptComp, DemocPolityComp, and FreeComp) are computed from functions with GDP per capita at PPP. In the case of conflict, the expected value is set at the base year's value (and the comparison is reversed because lower conflict values contribute positively to MFP). A significant amount of the foundational work behind the forecasting of governance related variables including conflict can be found in Hughes et al. (2014).
2.5.3 Driver Cluster 3: Physical Capital
The logic of the physical capital cluster is again parallel to that of the human and social capital clusters and involves the comparison of an actual (that is, IFs computed) with an expected value. The formulation for MFPPC can take several forms depending on the value of a switching parameter (inframfpsw) but the standard form involves four contributions, from traditional infrastructure (InfraTradContrib), ICT infrastructure (InfraICTContrib), other infrastructure spending level (InfOthSpenContrib), and the price of energy (EnPriceTerm). The last term is included because higher prices of energy can make some forms of capital plant no longer efficient or productive.
In the case of this cluster only the expected value of the traditional infrastructure index (InfraIndTradComp) and the expected value of other infrastructure spending (InfraOthSpendComp) are computed as most other cluster elements are, namely as a function of GDP per capita at PPP. In the case of the ICT index contribution, the technology has been evolving so rapidly that there is not really a basis for an expected value with some stability over time. Instead, the expected contribution from ICT is computed using a moving average value of change over time, so that faster rates of change contribute more to MFP if the moving average expected value lags behind the actual. In the case of the energy price term, the expected value is set equal to the energy price in the first year of the model run. As with variables in other clusters, a single parameter links the discrepancy between actual and expected values to MFP. A significant amount of the foundational work behind the forecasting of infrastructure related variables including conflict can be found in Rothman, et al. (2014).
2.5.4 Driver Cluster 4: Knowledge Capital
Following the pattern of other MFP driver clusters, the one for knowledge accumulation includes terms that compare actual model and typical or expected values and use parameters to translate the differences into increments or decrements of MFP. In this case the three terms represent R&D spending (RDExpContrib), economic integration via trade with the rest of the world (EIntContrib) and the tertiary graduation rate in science and engineering (EdTerSciContrib). In the first and third cases the expected values (RDExpComp; EdTerGRSciEnComp) are functions of GDP per capita at PPP. In the second instance, there is no clear relationship between extent of economic integration and GDP per capita, so the model compares a moving average of trade openness (exports plus imports as a percentage of GDP) with the initial value of openness (because trade is computed later in the computational sequence for each year, the values of trade variables lag one year behind those of the production function). Given the extreme global range of trade openness, the elasticity term itself in this relationship is variable, with values decreasing when initial openness is greater (that is, countries that start with less openness gain more from the same percentage point increases in it). Given computational sequence, values of EDTERGRSCIEN and some of the other actual terms are lagged.
2.5.5 Parameterization and Interaction Effects
The aggregation of so many driving variables into the representation of total factor productivity raises two interrelated methodological issues: parameterization of each variable’s contribution to modification of the core computation of productivity convergence and the interaction effects among those contributions.
The IFs project efforts to address these issues fall into three categories: (1) looking to the literatures around the contributions to productivity of individual variables and clusters of them; (2) extended statistical analysis of our own across the multiple variables in the four clusters; and (3) an arbitrary reduction of especially large increments and decrements associated with any of the four clusters.
Attention to literature supports the development and use of IFs. With respect to parameterization of the contributions of variables to productivity change, that attention has been constant across time. Illustratively, Barro and Sala-i-Martin (1999: 433) estimated that a 1.5% increase in government expenditures on education translates into approximately a 0.3% increase in annual economic growth. Globerman (2000) reviewed empirical work on the private and social returns to R&D spending and found them to be in the 30-40% range; see also Griffith, Redding, and Van Reenen (2000). The Handbook of Development Economics (especially volume 2) is a rich font of information on the empirics of growth. Hughes (2005) documented the original creation of the structure and its parameterization based mostly on existing literature.
Hughes and Narayan (2021) documented an extensive statistical analysis of drivers of change in total factor productivity within the IFs project. Much of that work was focused on analyzing and addressing multicollinearity in an approach involving so many driving variables. The project has dealt in part with this by selecting conservative values for the parameters when studies indicate possible ranges of contribution of the variables to productivity and/or growth.
Another concern is that a very large or extreme advance by one or a small subset of variables could have inappropriately large impacts of productivity given the fundamental conceptual foundation of the approach in the notion that development involves widespread and reinforcing structural changes across many variables. To limit this possibility, we have created an algorithmic function (MFPContribAdj) that adjusts the multiple MFP contributions and dampens especially high positive or negative contributions among the four cluster terms (MFPHC, MFPSC, MFPPC, and MFPKN).
2.6 Correction Factors in Computation of Productivity Growth Rate
As elaborated earlier (Section 2.2) and shown again in the equation below, in computing the sector-specific stock of multifactor or total factor productivity (TEFF), the endogenous growth of that every year (MFPGROWTH) is the sum of four contributions. The first two of those discussed to this point are the Convergence Base Terms (from the productivity growth of the technological leader and the GDP per capita based convergence term) and the Conditional Convergence Modifications of those (tied to patterns of change in human, social, physical and knowledge capital). Given discussion above of those two, it is possible now to move to the third, Correction Factors. Those factors include a country- and sector-specific correction factor (MFPCORS) and a global correction factor (MFPGLOCOR). MFPCOR is a value added-weighted average across sectors of MFPCORS. The corrections to sector-specific MFPGROWTH are required to assure that the base rate of aggregate economic growth for a country/region that is unexplained by capital and labor growth in the model’s base year can be attributed to the representation of productivity.
The computation of MFPCORS in the base year has five steps:
1. Determination of each country’s basic propensity for annual economic growth (already done/explained and put into igdprcor, see Section 2.2). What remains to be done is the computation of sector-specific basic growth rates (SectorGr).
2. Initial calculation of sector specific MFP’s contribution to growth (MFPGROWTH) from that basic propensity by subtracting out the sector-specific capital and labor contributions to value added growth as predicted from SectorGr.
3. Initial calculation of sector-specific correction (MFPCorSI) factors by comparing that initial calculation of MFPGROWTH with the endogenous computations of the Convergence Base Terms and the Conditional Convergence Modifications.
4. Using the sector-specific corrections and base year value added terms to compute a global correction factor (MFPGLOCOR) that is not specific to country or sector as an extra check on matching all drivers of MFPGROWTH with global growth.
5. Final computations of country and sector specific correction factors (MFPCORS) for use in MFP forecasts of future years.
The following sub-sections elaborate these steps.
2.6.1 Specifying Long-Term Economic Growth Propensity by Sector
Although igdprcor represents total national economic growth, growth in value added will vary by sector. It may be especially different between agriculture and other sectors, but IFs does not have a strong sectoral growth database. There is reason to believe, in particular, that the growth in the agricultural sector is likely to be different from and normally less that than in other sectors. IFs internally computes a sectoral economic growth rate (SectorGR) that ties the estimated value added growth of the agricultural sector to the preprocessor estimated growth rate of yield (TGRYL). For higher-income countries (with a GDP per capita above $5,000) it sets the agricultural sector’s growth rate at that yield growth level; it assumes that lower income countries depend more heavily on expansion of land as well as yield and sets the sectoral growth rate at twice the yield growth rate (and at least half of igdprcor). For other sectors the growth rate is set at igdprcor. The resultant deviation of growth in agricultural value added from igdprcor is spread proportionately across all other sectors to assure no change in national total growth expectation. Because its earlier surge of growth has ended, an additional block of code bounds growth in all Chinese sectors at 8.5%.
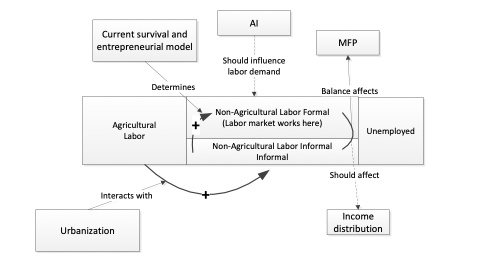
Attention to differential sectoral growth rates is important because of their differential labor productivity and the migration of labor across sectors. Many lower-income countries are experiencing a significant process of population migration from rural to urban areas with an associated movement of labor from agriculture to other sectors where that labor and associated capital produce more value added (albeit often with interim movements into the less productive informal economy, an issue returned to in Section 7). IFs represents these migration and labor shift processes. If the initial structuring in IFs of economic growth drivers including the correction terms within MFPCORRECT did not take them into account, forecasts of economic growth in years after the base year would very rapidly accelerate beyond the core rate imbedded in igdprcor. In fact, even with attention given in the base year initialization to adjustments of SectorGR representing this intersectoral growth accelerating process already underway and therefore showing up in igdprcor, growth projections for many lower-income countries in IFs show further acceleration of economic growth across much of the first half of this century. These model formulations will benefit from continued attention and review to understand the degree to which such acceleration is an insight rather than a weakness in representation.
2.6.2 Calculation of MFP Growth by Sector
Given an estimate of sector-specific, long-term growth propensity for value added (SectorGR), it is possible to compute a “predicted” time-independent value added VAddPred) as that of the base year plus that core value of sectoral growth.
Given this expectation for sectoral growth, to compute the contribution of MPF to that growth by sector (MFPGROWTH) we must also estimate and back out the long-term contributions of the capital and labor terms in the Cobb-Douglas function to sectoral growth propensity.
In aggregate for a country, the long-term growth rate in capital stock is determined by the ratio of gross capital formation (IGCF) to GDP, which covers both depreciation of and addition to capital. IFs uses a function called “Investment Ratio Versus Capital Growth Rate” to compute a total country-specific rate of growth for capital stock (KGroComp), net of depreciation, and assigns that to each sector (KGroCompS). During project tuning with the model it was determined that the value produced by the stylized function was too high; it is arbitrarily cut in half with the sectoral calculation.
The need to adjust the net capital growth estimate appears to have roots in three limitations that additional data on sectoral capital stock, investment, and rates of change in value added would help address. The first limitation is related to the use of the above function based on aggregate national investment rate for computing estimates of the net change in sectoral capital stock. Ideally, we would want to begin with historical data on sectoral capital stocks. The second limitation is estimating gross investment to sectors (IDS), together summing to gross aggregate national investment (IGCF), based on sectoral value-added shares of the total national value added. Ideally, we would also want data on sectoral investment. The third limitation is the use of those sectoral investment values to compute sectoral capital stock in the first year; that is done using sectoral depreciation rates as the inverse of the sectoral lifetime of capital (lks) and the sectoral estimates of net change in capital stock (KGroCompS).
The good news is that having these initial conditions and relationships, even if not as strongly rooted in data as desired, it is possible to compute an estimate of the propensity for contribution of annual change in capital stock to economic growth (KContrib). That estimate needs to use a value also for the Cobb-Douglas parameter on capital (PCDAlf).
Moving to labor, the long-term propensity for growth rate in the size of the labor force (LfGr) is primarily determined by the growth of population (POPR), the initial share of females in the work force (FemShrLabI), and the growth rate of the female share (FemShrGr).
Having rate of growth of the labor force allows computation of labor’s propensity for contribution to sectoral value-added growth in the same way as is done for the capital contribution, but it uses the forward-looking labor term parameter (1-PCDAlf). A small adjustment term is added to the basic growth of labor to capture the slow increase in skilled labor share (LabFGroRateAdj).
Finally, having (1) sectoral value added that long-term growth would be expected to generate and (2) the anticipated contributions to that growth of capital and labor, it is possible to isolate the growth rate that would be necessary from MFP (MFPGROWTH) to generate the predicted value added given core sectoral growth rates.
2.6.3 Computing an Initial Country and Sector Specific Correction
At this point it is possible to compute an initial estimate of the country-sector specific correction factors (MFPCorSI) because all of the terms that are supposed to drive MFPGROWTH in future years have been determined. These include the Conditional Base Terms, namely the technological or MFP growth rate for the leader (mfpleadr) and the convergence premiums for countries (MFPPREMIUM), as well as the four elements of Conditional Convergence Modifications (increments or decrements from MFPHC, MFPSC, MFPPC, and MFPKN, driven by many other variables of the IFs system).
2.6.4 Computing a Global Correction Term
The sector-specific, value-added weighted sum across countries and sectors of these discrepancies in calculation of MFP contributions relative to the calculation of the MFP growth to be explained will inevitably be non-zero given the many factors that underly the forecasting of economic growth and the many uncertainties around each. It could well be that there are systematic issues/errors in the formulation. One way of knowing that and of building in a correction is to sum the entire country-sector set and to compute the percentage of global GDP (the sum of VADD) within a global error and correction factor (MFPGLOCOR).
2.6.5 Computing the Final Country and Sectoral Specific Connection
Adjusting for the global correction factor assures that the Base Case forecast of global growth will, at least in the early years, not be significantly different from that the recent years on which the calculations of igdpr (and therefore VADDPred and MFPGROWTH in the first year) were based.
After that global adjustment there will remain differences between the values expected for those of individual countries and sectors, and those will be maintained in the final version of the MFPCORS correction factor that is computed in the base year and used in calculation of MFPGROWTH in future years.
Thus, in the base year the following equation for MFPGROWTH will continue to hold.
2.6.6 Exogenous Parametric of MFP beyond the base year
In years beyond the base year, the model allows Exogenous Interventions (adjustments) to MFPGROWTH. There are three parameters (with zero values as the default) that allow the model user much additional control over assumptions of technological advance. The first is a basic parameter (mfpbasgr) that allows a global growth increment or decrement; the second is a parameter (mfpbasinc) that allows either a constant rise or slowing of growth rate globally, year by year, where zy is the count of the model run years across time. The final exogenous term is a frequently-used parameter (mfpadd) allowing flexible scenario intervention for any country/region. The addition of these exogenous terms completes the formulation of MFPGROWTH to be used in years beyond the first, tying that formulation back to the initial introduction of it in Section 2.2 of this documentation.
In years beyond the first, the correction factor is gradually reduced to zero across time (the period specified by mfpconv) with the presumption that the full forecasting formulation is fundamentally strong and that even the 20-year base period on which igdprcor was based will have had its own idiosyncrasies. This convergence assumption has significant implications for model behavior because it tends (1) to slow down growth in countries (like China) that have had a burst of growth beyond that which the rates of the leader and the catch-up factor would lead us to anticipate and (2) to speed up growth in countries (like the transition states of Central Europe) that have suffered a reduction similarly unexpected by the basic formulation.
2.7 Monitoring Productivity Across Time
Additional variables in IFs facilitate the monitoring of elements of productivity across time. Most important is MFPRATE, which maintains all elements in MFPGROWTH except the four conditional convergence adjustment terms. MFPRATET is a VADD weighted sum of it for each country. Note: in the first model year MFPRATE is used in multiple steps in the creation of the MFPPREMIUM function, in the initial correction factor calculation, and in the final correction factor equation; the variables it incudes change across these steps, but its final calculation is consistent with the equation for subsequent years.
The model code for MFPGROWTH in years beyond the first uses MFPRATE rather than spelling out its components. Thus
where
Some additional variables facilitate monitoring of changing productivity levels:
MFPBAS is a country-specific average of MFPRATE values smoothed across time using a moving average of value added (SmVADD). Contrast it with MFPRATE, which uses annual VADD rather than SmVADD.
MFPCOR is a country-specific average of MFPCOR values smoothed across time using a moving average of value added (SmVADD).
MFPTOT is a sum of MFPBAS, the four conditional convergence modification terms and MFPCOR.
2.8 Issues and Modifications of Productivity and Growth
2.8.1 Changing Factor Contributions and Returns: CDALF
The Cobb-Douglas exponent (CDALF) of the production function is known to change over long time periods, generally giving somewhat less weight to capital (and therefore less return to it) as an economy becomes more capital intensive and therefore richer (see, for instance, Thirlwall 1977: chapter 2).
The GTAP project data provided the basis for an estimation of this relationship. The resultant cross-sectionally estimated function, in combination with data on sectoral differences in capital share, allow the computation of sectoral capital shares (AlphaS), normalized (with value added VADD) so as to generate CDALF for the total economy. A parameter (salpha) represents a generic pattern of capital share variation across production sectors.
where
Because the Cobb-Douglas exponents affect not just the relative contributions to production capital and labor but also the shares of GDP that firms and households receive, it will also significantly affect the financial flows within an economy, an issue to which we return in the discussion of the social accounting matrix.
2.8.2 The Relationship of Partial Equilibrium Models to the General Model
IFs normally does not use the economic model's equations representing MFP and production for the first two economic sectors, because the agriculture and energy models provide gross production for them (unless those sectors are disconnected from economics by setting the agon and/or enon parameters to zero). Instead, the two physical models provide gross production, translated to value terms with prices, back to the economic model. A later section of documentation (see 3.1.1.2) provides discussion of gross production and its relationship to value added and intersectoral flows.
In addition to this impact of the physical models on the production side of the economic model, there is one more of importance. Physical shortages of energy may constrain actual value added in each sector (VADD) relative to potential production. Economists typically do not accept such shortages as a real-world phenomenon because (at least in theory) prices rise to clear markets; yet during periods like the 1970s when governments intervened in those markets, such shortages do appear and they can in some IFs scenarios. In those situations, IFs assumes that energy shortages (ENSHO), as a portion of domestic energy demand (ENDEM) and export commitments (ENX), all calculated in the energy model, lower actual production in all sectors through a physical shortage multiplier factor (ShoMF). A parameter/switch (squeeze) controls this linkage and can turn it off.
where
2.8.3 The Economic Impacts of Climate Change
The energy and agriculture models (documented separately) produce carbon dioxide emissions from fossil fuel usage and changes in forestation levels that raise atmospheric levels and global temperatures (WTEMP). The changes in WTEMP have direct impact on agricultural yields, as does to a lesser degree the carbon fertilization of increased atmospheric levels. This passes through to agricultural production levels and enters the economic model as gross production of the agricultural sector, as discussed earlier. In addition, rising temperatures have complex implications for the broader economy, the focus here (see also Hughes 2019).
An issue that representations of climate impact in dynamic models must address is the extent to which damage to the economy occurs only in discrete time periods and the extent to which damage in any given year carries forward with implications for future years also, thus compounding the impact over time. In modeling it is simple to represent damage with a multiplier on the production function affecting each period’s GDP individually, and Nordhaus (2016) has taken this approach with DICE. Economic damage in a single period can, however, lower investment, and therefore capital stock and knowledge in the longer term (although it can also be argued that such damage often mobilizes unused resources, an element of adaptation). Elaborating cumulative and compounding impact, Dietz and Stern (2015: 579–580) argued that climate-related economic damage directly affects and reduces the stock of existing capital (e.g., direct damage to it or abandonment in instances such as sea-level rise) and even associated multifactor or total factor productivity (TFP). Use of a model like DICE or FUND with the addition of capital and productivity stock damage to that affecting annual production (a flow) can considerably increase the assessment of potential climate change cost at end of century to as much as 20 percent of GDP (Stern 2007, using PAGE02). An OECD study (2015: 81–84) also addressed this issue. That study’s analysis, using a version of the DICE model and directing 30 percent of annual damage to TFP and the rest to annual GDP, reduced annual GDP at the end of the century relative to a no-impact baseline by about 11 percent.
In IFs a switch (climeconimpsw) turns on the impact of climate for the nonagricultural economy. That switch, set on by default, activates a statistically aggregated approach for impact of warming on sectors of the economy other than agriculture (the impact of climate change on crop production and gross agricultural production is computed in the agriculture model and fed to the general economic model as described earlier). For non-agricultural and non-energy sectors IFs computes the magnitude of economic damage (CLIMECONIMP) resulting from the change in global temperature (WTEMP) relative to the temperature of the initial model year. The formulation is similar to the quadratic equation of cost-benefit models like FUND, DICE, and PAGE and computes the damage as a percentage of GDP, using linear and quadratic terms. The parameterization for those two terms (climeconimplin and climeconimpsq) looks to the work of Nordhaus and others. CLIMECONIMP is actually computed in the IFs environmental model, but we show that computation here because of its important use in the economic model in adjustment of both value added and productivity.
The damage reduces value added (VADD) by sector (which is an annual flow term), relative to the previous computation of it in the Cobb-Douglas function (reported below as VADDPrev, but in the IFs code VADD is on both sides of the equation’s code line).[1]
The difference in the equation above between climate impact in the current versus the first year of the model is actually carried inside the model via an internal variable (ClimImp) and put into ECGRCLIMGDP to help users of IFs see the size of the annual impact.
As discussed, it is possible that climate-related impacts are not only on annual production (with some future impact via reduced savings and investment), but also directly on capital stock and/or total factor productivity (TEFF). IFs uses another parameter (climeconimpstk) that is turned on by default to represent the portion of economic damage that might affect productivity as previously calculated (TEFFPrev) and driven over time by MFPGROWTH. Because TEFF is a stock term, the change in it is driven by year-to-year differences in the level of economic impact. The magnitude of the accumulated parameterized impact of climate change on TEFF is shown to the model user in the variable ECGRCLIMTEF.
IFs does not deal well with some of the challenges that face all modeling of climate change impact. For instance, it does not explicitly represent the impact increased weather volatility or extreme events, although those affects can be presumed to appear in the broader logic of climate impact via the parameterization of it from sources that do focus on the broad range of climate impacts.
With respect to time horizons, most analyses of climate impact on the economy stop at 2100 as does that in IFs. But atmospheric carbon increases will persist much longer. It is for this reason that analysis with FUND can extend through 3000 and that with PAGE through 2200. A central purpose of those models is to determine the social cost of greenhouse gas emissions, often conceptualized as the long-term cumulative cost per ton of current carbon dioxide equivalent emission, with final values often computed by applying a discount rate to future costs. The purpose of the analysis of economic impacts in IFs is to close the loops that connect the economy, climate change, and all other models in the IFs system.
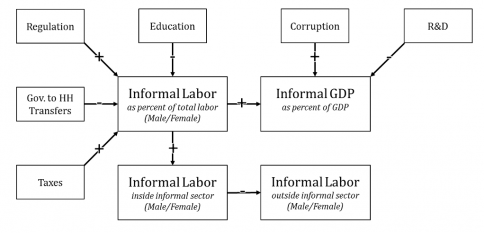
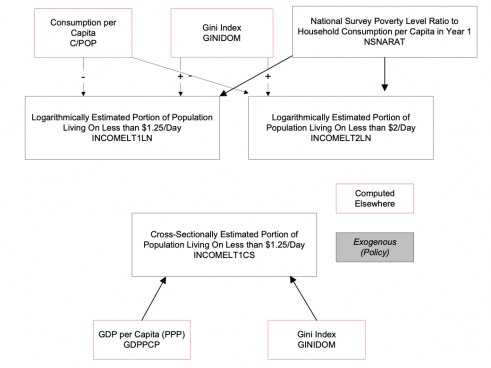
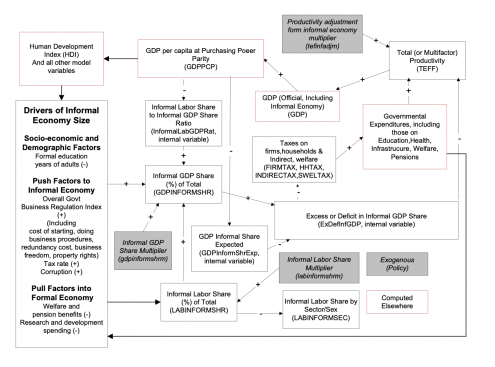
2.8.4 The Economic Impacts of the Informal Economy
Section 7 of this documentation details the representation of drivers of the informal economy. Here we focus on the effects of that informality on economic productivity and therefore growth. Whereas climate change is progressing from a relatively low base of impact and therefore is affecting both immediate GDP and underlying productivity patterns that historically were less or even little affected by it (for instance, little impact on igdprcor), economic informality has long been with us and is already baked into historical levels and growth rates of GDP. Thus, the representation of climate change economic impact in IFs significantly builds on absolute levels of it and represents the impact of increase in those for both GDP and productivity, whereas the representation of informality impact looks much more to changes (and often reductions) of that impact on productivity alone, letting those impacts then pass through to GDP.
We have structured the forward linkages from informality so that the model user can drive them with either the size of the informal economy (GDPINFORMSHR) or the size of the shadow economy (GDPSHADOWSHR) with differences in concepts and database described in their documentation. The logic of economic impact is the same in either case. Which concept and forecasts of change are used depends on the value of the shadow economy switch (gdpshadowon). If that parameter is 0 (the default) the driver is the informal economy share; if it is 1, the driver is the shadow economy share.
The fundamental driver of changes in economic productivity is the excess or deficit in the informal GDP share (ExDefInfGDP), relative to an expected value. This approach thus has much in common with that of modifications to productivity related to human, social, physical and knowledge capital.
We elaborate here the manner in which that excess or deficit affects total (or multifactor) productivity. Section 3.4.1.2 within the subsequent documentation of the social accounting matrix will then turn to the manner in which it affects taxation and therefore government revenues and expenditures.
The key to the productivity linkage is to recognize that an informal economy (or a shadow economy but to a much lesser degree) has the tendency, particularly in developing countries, to generate an official GDP that is lower than the potential GDP (PotentialGDP), because labor is employed with less capital and less efficiency in the informal sector. The magnitude of this productivity cost of informality (InfCost) can be illustrated by the fact that the data for some economies suggest that while 60 percent or more of labor can be informal, only 20 percent of GDP might be informal. This illustratively suggests that each unit of informal labor in such a country is used only about one-third as productively as is formal labor (we compute the ratio as the inverse, suggesting that each surplus unit of informal or shadow economy in this example could have a productivity cost of 3; we further bound that ratio so that it cannot exceed 3 or fall below 1, not shown below).
If gdpshadowon=0 then
else
It is important to emphasize, however, that the productivity and GDP growth rates in the basic IFs model already reflect the size of each country's informal GDP share and whatever drag or boost that share is giving to growth. Moreover, normal patterns of change in the informal GDP share (and that the share tends to decrease over the long-run with advance in adult formal education and/or GDP per capita), are essentially already built into the long-term dynamics of productivity change in IFs, for instance the basic growth rate and the conditional convergence or catch-up of productivity in developing countries with higher income countries. Thus, our attention here is not to the basic impact of informality on growth, but the incremental impact that deviations from the normal or expected size of the informal sector and the normal or expected change in that size might have on productivity. We can refer to such deviation as excess or deficit informal GDP share (ExDefInfGDP).
This point is so important that it bears rephrasing and repeating in only slightly different language. Why is this excess or deficit important? The dynamics of the IFs system's basic forecasting of economic productivity and GDP and of government revenue and expenditure patterns are all built on historical patterns and estimated functions that represent the normal processes within countries of gradual reduction of informal economy size with socioeconomic development. Thus, a normal decrease over time in the informal economy size should not be allowed to further affect the dynamics of productivity (or government finance). Similarly, if a country has a persistent and stably larger or smaller informal economy than would be expected at its level of socio-economic development, with GDP per capita at PPP serving as a proxy for that—it should have normal productivity and finance dynamics. It will be countries that change the share of the informal economy relative to their expected values with development, and that therefore demonstrate changes in the excess or deficit of the informal GDP share relative to expected share (ExDefInfGDP) that will alter their expected development pattern.
To compute the excess or deficit informal share we need only to explain the calculation of the expected share (GDPInformShrExp). That calculation uses a function estimated against GDP per capita at PPP, namely "GDP/Capita (PPP 2011) Versus Informal Share of GDP (Most Recent) Log." The same is true for the shadow economy and its share.
Over time this expected level is then subtracted from forecasts of the informal share, and the difference is divided by 100 to calculate the excess or deficit (ExDefInfGDP) in the extent of informal activities in ratio rather than percentage terms.
If gdpshadowon=0 then
else
What might be the potential GDP of an economy with an informal share that is larger than expected? We can calculate that by multiplying the Official Economy (GDP) by the excess or deficit share (ExDefInfGDP) and by the unit informal cost (InfCost), adding that to base share of the official economy—the base share is the official economy minus that excess or deficit informal portion and should not be understood to be entirely formal, but rather to be the expected core mix of formal and informal. Important Note: For ease of understanding, the equations shown below, down to the calculation of TefInfAdjustFac, are presented with a discussion of variables PotentialGDP, OfficialGDP, and TefInfAdjust that are not actually used in the code; but the underlying logic of the code and the presentation here are identical.
To illustrate this more concretely, if a country had an official economy of $100 billion, but 20 percent of that were "excess" informal economy, the base economy would be $80 billion. If the unit cost of excess informality were a factor of 3, the excess $20 billion of informal economy could potentially (were it formalized without additional implications, which it will have and which are also represented in IFs) become $60 billion and boost the potential GDP to $140 billion. Thus the calculation of the potential GDP in the formula above would be 100*(1-0.2) + 100* 0.2*3 = 80+60=140.
For the calculation further below of impact on productivity of reducing (or increasing) this potential GDP, we need a ratio of the official to potential GDP and will need to look at that ratio over time. Getting that ratio only requires a re-ordering of the terms in the above equation:
We call the ratio of official to potential GDP the (potential) adjustment factor for the total factor productivity and thus economy (TefInfAdjust).
Again, we can clarify by extending our concrete illustration above. For that economy the right hand side is 1/((1-0.2)+0.2*3)=1/(0.8+0.6)=1/1.4=0.714. Assume that the country were able to reduce its excess informal economy to 10 percent. The equation would then become 1/((1-0.1)+0.1*3)=1/(0.9+.3)=1/1.2=0.833.
If the country accomplished this reduction (which might take 10 or 20 years to do, of course), what would be the impact on economic production? Basically, it should be able to boost the overall magnitude of production by 0.833/0.714=1.167, that is, by 17 percent.
The change in the official/potential ratio from year-to-year (TefInfAdjustFac) is what will affect the stock of productivity and economic growth. The model user can also modify the impact with an adjustment multiplier parameter (tefinfadjm).
In the model code, we then feed that change (TefInfAdjustFac) into the variable that the model maintains for total factor productivity (TEFF). That variable is a stock, so that it carries over from year to year and has been adjusted already by other drivers of productivity before it is adjusted below by the informal economy term. Thus, our example country making a 10 percent reduction in excess informal GDP over 10 years might actually make a 1.6 percent change for each of the 10 years. Those annual changes would cumulatively affect TEFF in such a way that after 10 years, the total impact should be roughly that of the 17 percent computed above (roughly, because compounding and internal model dynamics would change that somewhat). TEFF is maintained by economic sector (s), so the changes in informality relative to expected values are implicitly assumed to affect all sectors identically.
The variable TEFF is a multiplicative term in the production function and the computation of value added and GDP. Thus, any change in TEFF feeds through to GDP in the same proportion.
2.9 Exogenous Control of Economic Growth
While IFs can endogenously compute economic growth for all countries and all years, there are at least two circumstances that call out for exogenous overrides of such computation: (1) when data exist for economic growth in the early years after the base year of the model; while the Pardee Center regularly advances the base year as new data become available, the IMF, other organizations, or national governments often have released data or estimates for some subsequent years; (2) analysts wish exogenously to specify GDP growth rates for future years and/or countries in order to explore the secondary effects of those; for instance, in exploration of the five Shared Socioeconomic Pathways (SSPs), which are often used in analysis of climate change, sets of exogenous GDP series exist for them across all countries through 2100.
In both cases, the mechanism for specifying GDP growth exogenously is use of the parameter gdprext (GDP growth rate, external), which overrides the model calculations whenever its value is greater than -65 (minus 65%). The preprocessor sets the value to minus 100 whenever there is no country-year value for GDP in the data series table where it looks for GDP values (e.g. SeriesGDP2011 for model runs using the GDP series based in 2011 dollars). Users of the model can also specify values greater than -65 in any scenario (.sce) file or via the scenario interface form of IFs.
Even in years for which economic growth is specified exogenously, the model needs to advance its calculation of labor supply (driven by demographics and participation rates as explained in a subsequent section of this documentation) and capital stock (changed with investment and depreciation). Theoretically it would be possible to assign the explanation for any discrepancy between endogenously and exogenously computed growth rates to either of those stock variables. Instead, given the wide range of forces that affect change in total factor productivity, the change in growth needed to accommodate an exogenous growth rate discrepancy is assigned to it (TEFF).
The absolute value for GDP increase or decrease that would be generated endogenously without an exogenous override is always first put into ActualGDPInc. The absolute value of GDP increase or decrease needed (across all sectors) to assure the growth rate specified by gdprext is computed by applying that exogenous rate to the sum of the value added terms from the previous year (because GDP is equal to the sum of value added terms across all sectors). That exogenously generated value is put into NeededGDPInc.
The difference between NeededGDPInc and ActualGDPInc is assigned to the productivity growth of the various sectors so as to achieve gdprext. This assignment is made in IFs, however, only to productivity levels in the “non-physical” sectors. That is, no adjustments for exogenously specified GDP growth rates are applied to productivity or production levels in the agriculture and energy sectors, where their growth rates can if desired separately be changed by other parameters in the respective partial equilibrium models. Thus, the difference between NeedeGDPInc and ActualGDPInc is put into a variable representing the absolute adjustment needed in the nonphysical sectors so as to generate the exogenous growth rate (NeededNonPhyAdj). Dividing that value by the sum of the endogenously computed value addeds of only the non-physical sectors generates a ratio (AdjGr) of change needed in those sectors (AdjGr is put into GDPADJ so that model users can see the adjustment size). To account for that change in TEFF requires only a multiplication of it by 1 plus that ratio. If the feeding of physical information from agriculture and/or energy to the full economic model is turned off, which is not the case by default, the adjustment can be spread to those sectors also.
s = 3,4 ... nsector, if agon and enon = 1; s = 1,2 ... nsector if agon and econ
2.9.1 Early Years
The Pardee Center routinely draws upon releases by the IMF of the World Economic Outlook to pull in its database estimates of GDP growth rates in recent years and for a few years into the future (generally 3-5 years). The data preprocessor of IFs uses those estimates to specify values of gdprext for those years. Unless scenarios like the SSPs specify values for GDP and/or its growth for years beyond the horizon of the IMF, the model then resumes computing economic growth (GDPR) endogenously
2.9.2 Long Term Scenario Analysis Including SSPs
In the same manner that IMF growth estimates can be put into IFs to exogenously specify GDP growth forecasts for the early years of scenario runs with IFs, other scenario sets can determine growth for longer periods. Using the ENV-Linkages model, the OECD has provided five sets of projections for the Shared Socioeconomic Pathway scenarios (SSPs) that extend through the 2100 horizon of IFs. Prepackaged .sce files (see SSP1.sce, etc.) exist in the IFs structure (a scenario folder) to run those projections in association also with demographic, education, income distribution, and other operationalizations of the SSPs for optional use.
Users can introduce other exogenous scenarios across the entire IFs run horizon as desired. The method for specifying a long-term GDP series is to set the parameter ifsexomodelid in an .sce file or via the model interface to a value other than the default of 0. That parameter will then be used inside the model (in a subroutine called ReplaceVarWithExogenousForecastxReg that sits in Function2) to access a table in IFs.mdb called IFsExogenousVars. Inside that table as of early 2023 were multiple lines for each of the 5 SSP scenarios. Each line in that file points for a specific variable in IFs (e.g. POP or GDPPCP) to a table inside IFsHistSeries that contains the exogenous SSP exogenous values for that variable. As of early 2023 there were 16 lines for each of the SSP scenarios, allowing those 16 variables to be overwritten exogenously in the model. Any new exogenous scenario added (e.g. using numbers “6” or higher, can point also to tables in IFsHistSeries for exogenous override of any or all of those variables. The code in IFs must, however, be written to accept exogenous override of any specific variable, so desire to exogenize any additional variables can require model code addition. In early 2023 there were numerous other scenario lines in IFsExogenousVars with pointers to variables to be specified exogenously for other projects underway within the Pardee Center.
A second parameter, ifsexomodeltype specifies whether the data series provided for exogenous use contain absolute values (=1) or annual percentage change (=2).
2.10 Short Term Shocks to Growth, as with COVID-19
The economic model of IFs was structured for long-term analysis. For that reason, the supply side is especially well developed via the Cobb-Douglas function and the elaboration of multifactor productivity change across time.
A capacity in IFs for representing shocks to economic growth was built in response to the COVID-19 pandemic in 2020-21. Although the logic developed is generalizable to other exogenously specified shocks in other years, the representation as of early 2023 is hard coded to that time period. The ability to introduce such shocks required model changes on the supply side (notably around the capacity utilization (CAPUT) term of the production function, a term that is not often in long-term economic models but was already in IFs because of its structuring to chase equilibrium across time rather than to reach it in each time cycle. It also required attention to the demand side of the model, notably to the response of household consumption and aggregate economic investment.
The internal variable COVIDShock turns the logic on (=1) or off (=0) to allow runs of the model with a No COVID scenario as well as with various COVID scenarios. COVIDShock is set to 1 in year 2020 (currently hard-coded) if the value of gdprext is less than 0 for the United States in that year.
Although IFs was built as a long-term forecasting system, GDP growth rates vary substantially across countries and years and can be negative. IFs was not, however, constructed to address the aftermath of a massive and widespread economic shock like those from economic crises or a pandemic. As indicated in a previous subsection of this documentation concerning the use of exogenous GDP growth rates, the variable representing the stock of total factor productivity (TEFF) accumulates the endogenously calculated portion of exogenously specified economic growth that is not accounted for by changes in capital stock and labor supply. Without change to that logic, a downward shock to GDP growth would persist in all future years because of its 100% absorption by TEFF.
Short of physical destruction in warfare, the economic impacts of even the most severe economic shocks cannot be represented entirely, and often not even largely, in terms of their elimination of labor supply, destruction of capital stock (although financial shocks can make some of it obsolescent), or reduction of the overall long-term productivity of labor or capital. Instead, shocks often interrupt production with reversable reduction of capacity utilization. IFs includes a capacity utilization term (CAPUT) in the production function that normally varies little across time. Coding for the COVID shock uses a parameter (tfpshockadjshr) that specifies the share of the shock that adjusts TEFF downward, assigning the rest of the shock’s impact to capacity utilization.
Reduction of both productivity and capacity utilization have longer-term implications. In the case of productivity reduction, a significant portion of it has indefinite duration. Another portion is, however, recovered over time because of the structure of the conditional convergence modifications in IFs. As laid out earlier in this documentation, most elements in that structure, including educational attainment of adults and life expectancy as a summary measure of health, contribute positively or negatively to productivity depending on their relationship to a value “expected” at their level of GDP per capita at PPP (represented in a cross-sectionally estimated relationship). Thus, a decline in productivity and therefore GDP boosts the net positive contribution of those elements (unless the shock also sets them back) and facilitates productivity recovery over time.
The mechanisms by which capacity utilization recovers are different and involve the larger set of dynamics around equilibration of supply and demand sides of the economy. (See the later documentation in this manuscript of the social accounting matrix structure and of equilibrating dynamics.) In general terms, there is some moving average-based inertia in the representation of household consumption behavior. A reduction in growth of production and household income from labor associated with it therefore does not reduce growth of consumption as much; the result is some reduction in inventories. That feeds forward to both increased prices and to higher capacity utilization via structures that use an equilibrating structure in IFs elaborated later in this manuscript to chase equilibrium; both rising prices and capacity utilization help boost production and replenish inventories. With the introduction of the capability to represent short-term shocks to capacity utilization via the tfpshockadjshr parameter, the structure around CAPUT was enhanced to increase its equilibration contribution. Specifically, the adjustment to capacity utilization is subsequently smoothed in a function named CapacityUtil (itself calling a function called ADJSTR to assist in the smoothing).
With the same logic, a bounce back of capacity utilization can in some instances also give rise to a surplus of production relative to consumption demand, potentially setting up oscillatory behavior (as in business cycles). Yet, in some sectors (such as services), inventories are difficult or imspossible to build and carry forward; thus, the representation of reaction to supply shocks also motivated a new algorithmic structure to depreciate/eliminate inventories above desired levels. Further, investment behavior can often be perversely disequilibrating in the face of capacity surpluses, because reduced prices and interest rates can lower incentives to invest; reduced investment lowers demand for goods and services, further raising inventory stocks. Model structure was somewhat adjusted to represent implicit “look ahead” capacity to respond to higher inventories from shocks with rising investment, thereby helping to absorb the surpluses.
The IFs system remains long-term oriented, but the use of tfpshockadjshr is an important augmentation of that orientation. Use of it in future shorter-term analysis would require attention to the hard-coded setting of the COVIDShock variable and of the years of that shock.
2.11 GDP at MER and PPP
Gross regional or national domestic product (GDP) is the sum of value added across sectors, which needs to equal the sum of production for final demand across sectors (see the later discussion of the social accounting matrix).
The GDP per capita (GDPPC) at market exchange rates (MER) and the economic growth rate (GDPR) follow easily.
The basic GDP figures for the model are represented in constant dollars of a particular year and at official exchange rate values. It is important, however, to forecast the value of GDP and GDP per capita at purchasing power parity levels as well (GDPP and GDPPCP). Although data releases of purchasing power data are done only periodically and are associated with particular years, they reflect a constantly ongoing process of change in the relationship of MER and PPP data that long-term forecasting should reflect.
To do that in IFs we compute a country-specific purchasing power parity (PPP) conversion variable (PPPCONV). Data sources provide values for the model’s base year. IFs uses a cross-sectional analysis-based analytic function that relates GDP per capita at MER to that at PPP to compute change in the conversion value over time. This is a generally unique feature in IFs because most long-term economic models maintain a constant relationship between GDP at MER in constant dollars and PPP based on the year set for the constant dollar value of GDP; those models change the relationship only when they change the constant dollar value year. As suggested, the actual relationship in countries around the world between MER and PPP value changes continuously.
As GDP per capita of a country converges with that of the system leader and the country becomes more active in the global economic system, the ratio of GDP at PPP and that at MER (which can be considerably above 1.0 for low-income countries) tends to erode toward 1.0. In IFs the calculation of PPPCONV is the product of two terms (BaseRatio and ConversionRatioCurrent). The BaseRatio builds on a ratio from the base year of the data-based GDP per capita at PPP to the value that is produced by the cross-sectional function (“GDP/Capita Versus GDP/Capita at Purchasing Power Parity (2000) Power Function”). It is thus what in IFs is often referred to as a multiplicative “shift factor” and can represent peculiarities for the country of the base year or data limitations that tend to disappear over time (a statistical “fixed effect” the drivers of which change over time); hence we converge it toward 1.0 over 100 years. The ConversionRatioCurrent responds to changes in GDP potential per capita (at MER) over time (actual GDP per capita having not yet been computed in the flow of model calculations) and will automatically tend to converge to 1.0 as the GDP per capita of countries move closer to that of the system leader, the United States.
GDP (and its value-added shares) take a third form in IFs called “relative-price adjusted” GDP or GDPRPA. The SAM section of this documentation explains and uses this form.
2.12 Indicators
The economic model computes several indicators of interest to many IFs users. These include global product (WGDP), global product per capita (WGDPPC), an absolute measure of the per capita GDP gap between more developed (D) and less economically developed (L) regions (NSGAPA), and a ratio measure of the same gap (NSGAPR). A parameter (nsdiv) establishes the GDP per capita at MER dividing point in thousand constant dollars between more and less developed.
In an algorithmic procedure the system also computes a ratio of the GDP per capita (MER) in the countries that by average GDP per capita make up the richest 10 percent of global population to those that populate the bottom 10 percent (NSGAPRTB).
2.13 Methodological Note: Algorithmic Adjustment of Forecasts in IFS
Economic growth rate in the goods and services market is only one area in IFs where specification of initial values for variables using formulations (statistically estimated or based on standard computational structures) often produces values that differ from historical data in the base year. That is the first of three challenges for forecasting across the time horizons supported by IFs. The second is that computations using such formulations can generate patterns of change in early years of forecasting that differ substantially from patterns evident in the data from recent years. Third, it is very common in the long term that formulations generate problems including exceeding reasonable limits (e.g. percentage values below zero or above 100%), failing to saturate smoothly to such limits, or saturating at values that exhibit unreasonable patterns across the 188 countries of the IFs system.
There are many reasons for such forecasting challenges. There are also a variety of approaches for addressing such issues, but in general terms they require building algorithmic structural wrappers around even the best estimated and/or most strongly grounded theoretical specifications. The subsections below consider the three challenges sequentially by time horizon.
2.13.1 Initial Condition-Related Forecast Challenges
Calculations by IFs in the model’s base year, even using formulations estimated with high statistical significance, will almost invariably produce values that differ from data. These are essentially the country-specific residuals in the estimation or more theoretically founded specification. There are a variety of explanations for and treatment of those residuals in correction of those discrepancies in the first year and forecasting over time.
In the base year itself, it is simple to compute either an additive or multiplicative factor that adjusts the computed value to the base year’s data value and to protect the data value IFs almost always does that adjustment. In the IFs project these have been labeled “shift factors” internal to the model and in documentation. Additive shift factors are heavily used and are more easily understood to be the residual term between the value of a variable in the model computed the first or base year and the data value for that first year. They are always the more appropriate of the two adjustments when a forecast variable can take positive and negative values (like net foreign aid receipts) or zero values. The key issue becomes what to do with those shift factors across time and that depends heavily upon the interpretation of them. Among interpretations:[2]
· Data for many of the variables in IFs are differentially and often somewhat poorly gathered by countries or other original sources; they may often even be estimated. Over many years processes for and quality of data gathering (e.g. via surveys) has tended to improve and that suggests the likelihood that such “poor data” residuals or errors will be reduced over time within the data source.
· There may be “fixed effects” at work. For instance, the status of women in a society can shift a country’s value on a variable (e.g. with respect to educational enrollment or fertility rates) away from the pattern captured in a function estimated across all countries. But what are often referred to as fixed effects in statistical estimation often do change and erode over longer periods of time like the century-long horizon of IFs. Many might better be labeled “eroding effects” than fixed effects.
· There may be “random effects.” For instance, the level of public spending on infrastructure within countries can move up and down as a percentage of GDP in response to changes in government leadership related to preferences of a political party or of specific personnel in leadership roles. In combination with fixed effects these are sometimes referred to in modeling as “mixed effects”.
· There very often is “omitted variable bias” within a model specification, the omission of variables that, often not even identified, cannot be categorized as fixed or random effects.
Based on substantive knowledge of the issue area and specific variable, a judgment can be made with respect to whether to leave the shift factor in place over the entire time horizon or to gradually eliminate it and move forecasts for the variable toward the general values of the formulation. As with the correction factor for productivity’s contribution to economic growth rates (MFPCORS), explained in a previous sub-section, a common representation in the IFs model is a gradual convergence of additive shift factors to zero or multiplicative factors to 1.0. The presumption underlying that convergence is that poor data gathering gradually improves, fixed effects tend to erode toward global patterns, and random effects average out over time. The time period for the convergence is inevitably a matter or subjective judgment hopefully substantively informed by consideration of the possible explanation for residuals, and most are set in IFs to be fairly long because data inadequacies and fixed effects in particular tend to be slow to change; longer periods also to avoid rather sudden and unexplainable shifts (or transients) in model behavior.
2.12.2 Early Year Variations From Historical Patterns
A second common temporal adjustment issue in forecasting is that values produced by a formulation in relatively early years (for instance through the period of the sustainable development goals or even to mid-century) can exhibit a trajectory different from the pattern of recent data years. This is a “growth-pattern transient” rather than a “base-year-value transient”. A large portion of the variables in IFs do not exhibit growth-pattern transients. This is because many of the core driving formulations for those variables are functions of GDP per capita at PPP and the patterns of change in those variables with GDP per capita are rather uniform across countries.
One formulation where this is not the case is the growth of GDP itself, tied in IFs to the Cobb-Douglas production function, as described in earlier subsections. Because the drivers of that function (including change in capital stock, active labor force size, and the wide range of drivers of multifactor productivity) are themselves so complex, and because economic growth is subject to so many random effects (e.g. fiscal and monetary policy or inventory accumulation across business cycles), it would be highly improbable that the formulations underlying economic growth would produce values for economic growth rates in early years that are highly consistent with the pattern of the years preceding the base year. For that reason, IFs uses data to compute an initial GDP growth rate parameter igdpr that averages across data from recent years and uses it to compute national and global correction factors within the Cobb-Douglas formulation to assure that the values computed in earlier years of forecasting bear a reasonable relationship in the base case run to the historical patterns.
A related situation that can complicate the generation of early year forecasts consistent with historical patterns is when statistically-estimated driving functions become very complex. For instance, the statistical estimation of variables using multiple drivers (e.g. educational attainment as well as GDP per capita) has value because it provides multiple handles for policy intervention analysis and estimation can have high statistical significance and explanatory power with respect to the historical data. Yet, many such driving variables can be highly correlated; the resultant multicollinearity can create model formulations that are subject to some instability with respect to forecasting, particularly if the addition of driving variables were to result in signs for some drivers opposite to what the drivers would have in simple relationship with the forecast variable (a formulation to be avoided).
In all such instances, formulations, whatever the combination of structural logic and estimation they are built upon, are likely to produce patterns of forecasted change over time that are inconsistent with historical patterns in the data unless there is some use in early model forecast years of information about those historical data. The forecasting system can benefit greatly from algorithmic structural wrappers that combine information about individual driver and/or forecast variables with others and with that historical information.
2.13.3 Longer Term Forecast Behavior Issues
Looking beyond issues around the base year of the model and the early forecast years, the longer-term poses another set of temporal model issues. Some of these are very simple, including the assurance that percentage variables do not fall below zero or rise above 100 percent. Such boundary conditions are used throughout IFs; in many cases hard boundaries have been replaced with algorithmic functions that smooth final approaches to those boundaries.
Other long-term issues are much more complex. For instance, when multiple dependent variables being forecasted have complex interrelationships, driver formulations, whether structurally built-up like that for GDP and its growth or statistically estimated, will often generate long-term results that can be inconsistent with historical patterns and/or inconsistent with other forecast variables within the interrelated set. Examples include government spending in any category (e.g. health as a focal point) when other spending (e.g. on education or infrastructure) must in some algorithmic way be integrated into the forecasting system of total spending. Another example is within education when spending patterns across primary, secondary, and tertiary levels have obvious trade-offs and countries may have quite different and idiosyncratic priorities. Still another is across categories in the ladders for water and sanitation when the advances in the percentage of population access to one category of access (e.g. to safely managed watsan) must always mean that there is a reduction in the percentage of population for whom highest ladder-rung access has in earlier years been a different category.
Among approaches to handling interrelated dependent variable sets in the long-term, simple normalization of all within the set to a total variable is common in IFs. That approach is used within government consumption; whenever a scenario increases one target (e.g. health), all categories can be normalized to total spending. Another approach is to give special priority to one DV within the set (e.g. safely managed watsan) and to adjust forecasts of other DVs in the set accordingly.
Household consumption in IFs illustrates another approach. It is common when forecasting household consumption patterns across different categories of goods to use Engel elasticities that indicate decreasing consumption expenditure shares on food, rising and then falling spending shares on manufactured goods, and rising spending shares on services. That approach was used across many generations of IFs, but it tended to produce rather different late-in-the-century patterns of expenditures for households in different countries even at similarly high levels of household income per capita, as well as nearly eliminating all spending except that on services. These results were in part because of weak data for initial conditions on household consumption patterns and in part because the basic approach with Engel elasticities was built primarily for forecasting efforts over shorter horizons. A better approach for IFs in the long run proved to be specifying a pattern of consumption across the economic sectors at very high levels of household consumption with converging national patterns to that target pattern as per capita consumption rises.
3 Social Accounting Matrix (SAM)
A social accounting matrix (SAM) integrates a multi-sector input-output representation of intersectoral flows within an economy into the broader system of national accounts (SNA), thereby broadly representing flows of funds among societal agents/institutions and, via the balance of payments, also with the outside world. Richard Stone is the acknowledged father of social accounting matrices, which emerged from his participation in setting up the first systems of national accounts or SNA (see Pesaran and Harcourt 1999 on Stone’s work and Stone 1986). Many others have pushed the concepts and use of SAMs forward, including Pyatt (Pyatt and Round 1985) and Thorbecke (2001). So, too, have many who have extended the use of SAMs into new frontiers. One such frontier is the additional representation of environmental inputs and outputs and the creation of what came to be known as social and environmental accounting matrices or SEAMs (see Pan 2000). Another very productive extension is into the connection between SAMs and technological systems of a society (see Khan 1998; Duchin 1999). It is fitting that the 1993 revision of the System of National Accounts by the United Nations began explicitly to move the SNA into the world of SAMs.
The SAM of IFs is an integral part of a dynamic general equilibrium-seeking model. The structural representation is a variant and to some degree an extension of the computable general equilibrium (CGE) model structures that often surround SAMs. In wrapping SAMs into CGEs, Stone was also a pioneer, leading the Cambridge Growth Project with Alan Brown. That project placed SAMs into a broader modeling framework so that the effects of changes in assumptions and coefficients could be analyzed, the predecessor to the development and use of computable general equilibrium (CGE) models by the World Bank and others. Some of the Stone work continued with the evolution of the Cambridge Growth Model of the British economy (Barker and Peterson, 1987). Kehoe (1996) reviewed the emergence of applied general equilibrium (GE) models and their transformation from tools used to solve for equilibrium under changing assumptions at a single point in time to tools used for more dynamic analysis of societies.
The approach of IFs is both within these traditions and an elaboration of them on five fronts. The first elaboration is in universality of the SAM representation. Most SAMS are for a single country or a small number of countries or regions within them (e.g., see Bussolo, Chemingui, and O’Connor 2002 for a multi-regional Indian SAM within a CGE). The IFs project has created a procedure for constructing relatively highly aggregated SAMs from available data for all countries it represents, relying upon estimated relationships to fill sometimes extensive holes in the available data (see documentation on the IFs data preprocessor, including that in Supplemental Appendix A). Jansen and Vos (1997: 400-416) refer to such aggregated systems as using a "Macroeconomic social Accounting Framework." Each SAM has an identical structure and they can therefore be easily compared, linked, or aggregated (e.g., for regions of the world).
The second elaboration is connecting the universal set of SAMs through representation of the global financial system. Country-specific SAMs generally treat the rest of the world as a residual category. Because IFs contains SAMs for all of its countries, it is important that their rest-of –the-world representations are mutually consistent. Thus, exports and imports, foreign direct investment inflows and outflows, international borrowing and lending by governments, and many other inter-country flows must be globally balanced and consistent.
The third elaboration is a representation of financial stocks as well as flows. Both domestically and internationally, many flows are related to stocks. Representing these stocks is very important from the point of view of understanding long-term dynamics of the system because stocks such as household financial assets, government debt, IMF credits, World Bank loans, reserve holdings, portfolio investment, and capital stocks facilitate and constrain future flows.
The IFs stock framework has been developed with the asset-liability concept of standard accounting methodology. The stock framework is an important extension of the normal social accounting flow matrix, and the cumulative flows over time among the agents will determine the stocks of assets or liabilities for all agents. If the inflow demands repayment or return at some point in future, it is considered a liability for that agent and an asset for the agent from which the flow came. For example, in IFs, if a government receives loans (inflow) from other countries, the stock of those loans is a liability for the recipient government and an asset for the country or countries providing the loans.
The fourth elaboration is temporal and builds on the third. The SAM structure described here has been embedded within a long-term global model. The economic module of IFs has many of the characteristics of a typical CGE, but the representation of stocks, flows, and related agent-class driven behavior in a consciously long-term structure introduces a quite different approach to dynamics. Instead of elasticities or multipliers on various terms in the SAM, IFs seeks to build agent-class behavior that often is algorithmic rather than automatic. To clarify this distinction with an example: instead of representing a fixed set of coefficients that determine how an infusion of additional resources to a government would be spent, IFs partially endogenizes such coefficients, linking them to such longer-term dynamics like those that shape the demand for government spending in the education, health, and infrastructure models of IFs. Similarly, the stock of household assets affects temporally dynamic division of income into savings and consumption. Section 4 will discuss how stocks of assets and liabilities help drive the behavior of agent classes in shaping the flow matrix.
The fifth and final elaboration has already been touched on. In addition to the economic model, the IFs forecasting system includes other models relevant to longer-term forecasts and SAM dynamics. For example, demographic, education, health, agriculture, and energy models all provide inputs to the economic model and SAM, as well as responding to behavior within it. The effort is to provide a dynamic base for forecasts well into the 21st century. It is important to quickly re-emphasize that such forecasts or projections are not predictions. Instead, they are scenarios to be used for building and exploring possible alternative longer-term futures.[1]
3.1 Structural Overview of the SAM and Representation in IFs
Two steps can lay out SAMs conceptually and provide an overview of the SAM structure in IFs. The first of those is an explanation of the input-output matrix foundation of social accounting matrices and the second is an elaboration of the full SAM structure. After completion of this conceptual and representational overview, the documentation will elaborate the SAM elements in turn for households, governments, and firms.
3.1.1 The Input-Output Table Foundation
3.1.1.1 Conceptual Structure: General and in IFs
The roots for accounting of financial flows reach back to Francois Quesnay’s Tableau économique in 1758 and Léon Walras’s work on general equilibrium theory in 1874, but it was Wassily Leontief who pushed forward the modern representation of the input-output table in Nobel prize-winning work (Leontief 1951). Table 3.1 is the OECD’s representation of the elements in an input-output table, which it describes as showing the “sale and purchase relationships between producers and consumers within an economy”[2]
An important part of the I-O matrix that connects the production and consumption elements is the square in the upper-left corner that represents intersectoral flows (37-by-37) in the OCED illustration and 6-by-6 for each country in the IFs system. Each column contains the input or “intermediate” requirements (in terms of expenditures for those inputs) used in the total production of the economic sector represented by the column total. Dividing each cell in that sub-matrix by the total monetary value of the production or output of the sector therefore generates a matrix representing the mixture and magnitude of inputs per unit of output, thus the production technology of the sector. In fact, the resultant coefficient matrix for the entire square sub-matrix is generally called the technology matrix and labeled as the A-matrix.
The difference between the sum of the absolute values in each column of the submatrix and the total production of the sector is the value added by capital and labor in the production process. That value added is what the Cobb-Douglas production function computes (see again Section 2.2) and that the alpha exponent in that production function divides between the firms and households that provide the capital and labor. As we shall see when we turn to the larger social accounting structure surrounding the I-O matrix, those returns to firms and households and their interactions with each other and with government and the outside world constitute the larger financial flows of the SAM.
One other important element of the SAM as shown in Table 3.1 from the OECD is the structure to the right of the intersectoral flow submatrix under the heading of “final expenditure.” The summed value in each row across the delivery of a particular sector’s goods or services to other sectors, to firms labeled as industry in the table (for instance, for investment in new capital stock), to households and government for consumption labeled as domestic demand, and to other countries via exports is the total value of the output production for the sector (equivalent to the sum of the rows for the sector’s inputs looking down that sector’s column). As the OECD figure also indicates, the output calculation of GDP as the sum of the value added (looking down columns) can be supplemented by the expenditure calculation of GDP as the sum of the deliveries of each sector to firms, households, government, and net exports.
3.1.1.2 In IFs: Gross production, intersectoral flows, and production for final demand
The discussion of the general conceptual structure of the input-output matrix provides the basis for explaining the approach in IFs for elaborating values of the matrix. In each country that approach requires a technology (sub)-matrix (A-matrix) representing the units of intersectoral flows in each column for each unit of production at the bottom of the column (including also the value added). We discuss below the endogenous calculation of changing A-matrices in the IFs approach (AMat), which differs from the more common exogenous provision of the matrices.
Given that technology matrix and the value added (VADD) in each sector from the production function, the standard approach for determining total or gross production (ZS) in each sector is to divide the value added by 1 minus the row sum of the column. The inverse of 1 minus the A-matrix is generally called the Leontief inverse.
The production functions of the partial equilibrium models for agriculture and energy provide calculations of ZS instead of VADD. When the agon and enon switches are turned on (the default, we therefore compute VADD using a reordered calculation of the equation above.
This reordered calculation is done following the calculation of VADD for all sectors in the economic model and the adjustment of sectoral VADD values by the impact of climate change (see Section 2.2 for discussion of that impact). In the agricultural model ZS is adjusted by the impact of climate change on yields and that adjustment will therefore pass through to the override calculation of VADD indicated above.
Given gross production and the A-matrix we can compute intersectoral flows (INTS).
One important variation to the use explained above of the A-matrices in IFs (with the basic dynamic determination of those matrices explained in the next subsection) is for the agriculture sector. In the partial equilibrium agriculture model some of the gross production of crops is directed explicitly to feed demand for animals (FEDDEM), back into producing crops via usage including as seeds (FMDEM), and into industrial uses such as cotton for fabrics (INDEM). These variables are essentially the intersectoral flows related to the usage of crop production. In the economic model the changing ratio (AgINTSFLows) of these to food demand for crops (FDEM) is a better, physically-based calculation of changing intersectoral flows within the agricultural sector than is the first row of the A-matrix. It therefore is used to change the base year’s value of the coefficients for the sector used in the above calculation of VADD and INTS.
Production available for final demand (PFD) is the residual of gross production minus the sum delivered to all columns in the intersectoral flow matrix. That variable, typically not given much attention in economic modeling, is important in IFs because comparing it with the actual level of final demand generated by other models and formulations in IFs determines the annual adjustment to inventory stocks. Those stocks are an essential variable in the model dynamics, as described in Section 4.
3.1.1.3 Computation of A-matrices
GDP per capita-linked generic A-matrices are created in the preprocessor of IFs. To build them the IFs project turned to the IO matrices collected in the Global Trade Analysis Project. That database includes extensive data, including IO matrices, for 127 regions/individual countries across 57 sectors in GTAP 8; every version tends to increase geographic coverage and sectoral numbers have risen. With origins in 1992 of the now global project at the agricultural economics department of Purdue, GTAP heavily represents agricultural sectors. Narayanan, Aguilar and McDougall (2012) documented GTAP 8 (see also earlier versions including Dimaranan and McDougall (2002) for GTAP 5). As of early 2023 and this writing, GTAP 10 was used in IFs and the release by GTAP of version 11 was imminent.
The preprocessor of IFs (Hughes and Irfan 2006; Hughes et al. 2020) processes the IO matrices of GTAP to create those needed by IFs. One aspect of that involves collapsing the sectors to those of IFs (currently 6) using a concordance table. Even more importantly, however, the preprocessor generates from the most recent GTAP files within IFs a set of nine generic IO matrices to represent the average technical coefficient pattern of countries at different levels of GDP per capita. The generic matrices are calculated as unweighted averages of matrices for all countries with GDPs per capita in categories established by lower-end breakpoints of $0, $175, $375, $750, $1,500, $3,000, $6,000, $12,000, and $24,000.
The assumption behind the generic IO matrices is that countries at different GDP per capita levels typically use different types of technology. The resultant IO matrices bear this out in ways that seem intuitively plausible. For example, Tables 3.2 and 3.3 show (using earlier data from GTAP 5) the technical coefficient matrices for extreme levels of GDP/capita, below $100 and above $24,000, respectively. Note, for instance, how much lower a share of manufactures goes into the agricultural sector in the richest countries relative to the poorest (reading across the rows), and how much more of the IC sector goes back into the IC sector in richer countries.
These generic matrices are used for two purposes. First, they are used for estimating values for countries of IFs that are NOT in the GTAP data set. Second, they are used in the dynamic calculations of the model. As countries rise in GDP/capita, interpolations between matrices above and below their level allow us to gradually change the technology matrix representing each country.
GTAP also provides data on return to factors of production in each sector, including land, unskilled labor, skilled labor, and capital. More recent versions of GTAP have expanded the number and type of households and labor, but because of the data challenges faced by GTAP in that elaboration the IFs project continues to collapse those into skilled and unskilled categories. These returns represent value added and are very important data for the value-added blocks of the SAM. The preprocessor also collapses GTAP production factor data into the economic sectors of IFs and computes generic shares of the factors in value added by GDP per capita category, using the same unweighted average technique used for the IO coefficients. Once again, the generic value-added shares are used both to fill country holes in the GTAP data set and to provide a basis for dynamically representing changes in those shares as countries develop.
The changes across the levels of GDP/capita appear reasonable. Note, for instance, the general shift of return to skilled from unskilled labor and the increase in returns to labor in total for the manufacturing and ICT sectors (at the expense of capital and other inputs).
The equations for value added and income in household categories can be found in our subsequent discussion of households as agents. Although the GTAP data by no means provide everything that was needed for the generation of universal SAMs, the GTAP fully understands the great utility of SAMs (Brockmeier and Arndt 2002) and provides several primary data inputs that serve our purposes and those of many other economic models.
Further, the GTAP data and the GDP per capita threshold approach is used in the preprocessor to compute a generic table for labor demand coefficients by sector, distinguishing skilled and unskilled labor. These are stored in the IOLaborCoefs table of IFs.mdb and are available for the computation of labor demand in the economic model. More generally, most GTAP data are stored in the IFs.mdb table of the system
3.1.2 The SAM Elaboration
In language from the OECD, the input-output table shows the “sale and purchase relationships between producers and consumers within an economy.”[3] Around that core, the broader social accounting matrix represents the multiple financial flows among the household, government, firm, and foreign actor agent categories. Again, it is useful both to consider that pattern of flows in stylistic aggregate form and to see the approach to representing them in IFs.
3.1.2.1 Conceptual Structure
Figure 3.1 begins to suggest the character of a SAM by portraying selected flows among the agent categories: households, enterprises or firms, government, and the rest of the world.
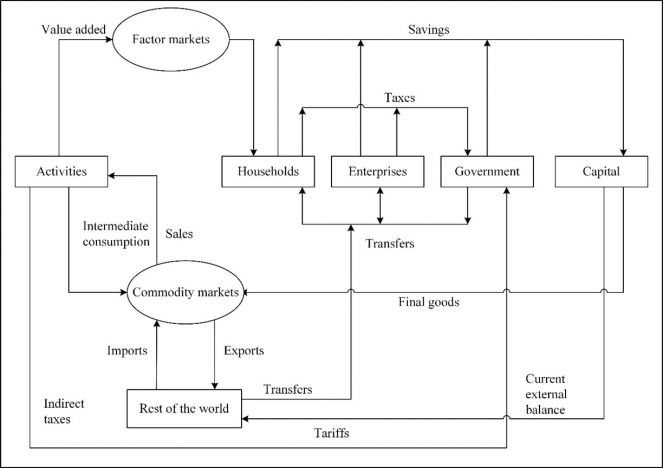
The stylized social accounting matrix in Table 3.6 elaborates the spectrum of linkages between the production (or activity) and expenditure sides of a socio-economic system.
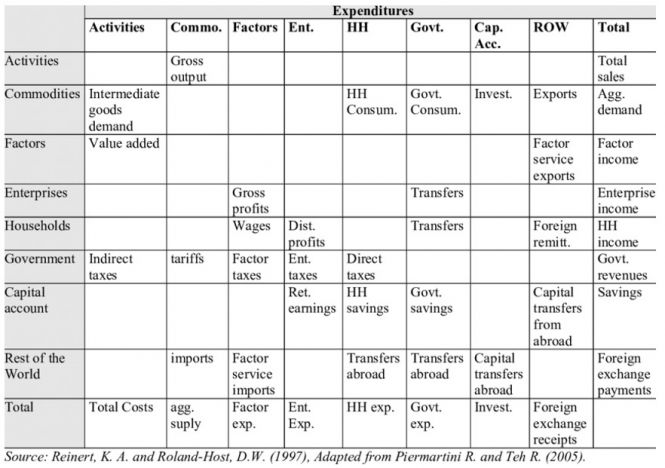
3.1.2.2 In IFs: The SAM
The SAM structure of IFs is much like that of Table 3.6. IFs presents it to the user at two very different levels of aggregation. Table 3.7 shows the highly aggregated form for India in 2025.
Tables 3.8A-C show the disaggregated form. Together the matrix across the three figures effectively shows almost all the different flows represented in IFs. The remaining subsections of this documentation section devoted to the SAM in IFs will focus in turn on the flows involving households, government, firms, and international actors.
Although this vast network of flows is fundamentally important to IFs, it becomes only meaningful in forecasting when placed in the context of dynamics generating temporal changes in them. The specification of them in the remainder of this section will lay the foundation for explaining the dynamics in IFs, and subsequent sections (notably Section 4 on equilibration dynamics) will elaborate them.
3.1.3 Relative price adjustment of value added and GDP
Although the IFs model represents prices in real terms (no monetary sector and no inflation), there are relative sectoral price changes (PRI). Some of those can be quite dramatic over time, especially in the agricultural and energy sectors where the equilibration of physical representations of supply and demand, in combination with dramatic changes in factor endowments such as fossil fuel resources, can swing those prices. Such relative price swings can, in the real world significantly raise or lower the value added in those sectors and for economies as a whole, especially for countries s heavily dependent on energy production and trade. Changes in relative prices in heavily exported sectors provide terms of trade gains or losses and therefore effectively higher or lower relative incomes to some countries than others. Consider what the sharp rises in oil prices did for oil-exporting countries in the 1970s and 1980s. Even in “constant dollars” their economies became effectively much larger, giving additional effective income and purchasing power to governments, households and firms.
It is impossible to understand changes in financial flows even in a model based in constant currency without representing those relative price changes. Commonly this might be done by juxtaposing real gross national income (GNI) with real GDP. The IFs system incorporates the international flows that undergird GNI. It calculates a variation of GDP often called real GDI or Gross Domestic Income that represents the impact of relative price changes across sectors (see Macdonald 2010). In IFs that is done by explicitly representing both relative-price adjusted value added (VADDRPA) and relative price adjusted GDP (GDPRPA) and using those terms rather than VADD and GDP in representations of social accounting within and across countries. GNI differs from GDP largely in terms of the accounting for financial inflows and outflows from abroad; those enter the IFs SAM in multiple ways, including the addition of foreign aid inflows to government revenues.
The relative-price adjusted version of value added is the normal value added from the production function weighted by world sectoral prices (WP); the prices are lagged a year because of the recursive model structure.
The sum of those adjusted value addeds across sectors produces the relative-price adjusted GDP (GDPRPA), effectively equivalent to real GDI. The utility of this variable can be seen, for instance, in countries, like Saudi Arabia, that are heavily dependent on energy exports. Large swings in the relative price of the energy sector can dramatically affect the relative-price adjusted GDP and national expenditure patterns. We therefore carry this variable forward from the goods and services market into the more encompassing social accounting matrix representation.
A further variation on GDPRPA is a potential calculation of it (GDPPOTRPA), which assumes full use of production capacity.
3.2 From Economic Production to the SAM: Household and Firm Earnings
The gross earnings of households (HHINCEARN) and firms (FIRMEARN) are the primary bridge from economic production in the goods and services market to the social accounting matrix. Those are determined by the shares of capital and labor in the production function, that is by the sector-specific exponents on capital (CDALF) and labor (1-CDALF when returns are constant to scale). That is, with an increase in both inputs by 1 percent, output would increase by 1 percent and, if CDALF were 0.4, 60 percent of the output rise value would be attributable to labor and, ceteris paribus, 60 percent of the added value would accrue to the households (across unskilled and skilled household types, h) providing that labor. Thus, a fundamental identity maintained by IFs is that:
where stylistically the following is true:
The computation of household and firm earnings is considerably more complex within IFs than in the stylized equations because household earnings by skill level (and thus possible changes in unskilled and skilled shares of earnings and societal income distribution) are built upward across sectors, taking into account the changing use of unskilled and skilled labor across sectors and the wages paid by skill level and sector. Specifically, an initial calculation of the household earnings by skill level and sector (VADDHHUi and VADDHHSi) is a product of the amount of labor employed in each sector (LABEMPS) and the wage rates by sector and skill level (LABWAGES).
The level and pattern of employment across sectors is endogenously determined across time in the labor market discussed later in this documentation. However, the wage rates by skill level within each sector (LABWAGES) are as of this writing computed only in the first year and the values not changed over time, thus keeping the wage rate differentials for skill levels within sectors constant. The first year’s division of wages within sectors by skill level (LABWAGESSHRSKL) is also constant across time after being built in the preprocessor from GTAP data (but only used in the first year’s computation of LABWAGES). Acemoglu (2002) suggests that the ratio of shares going to skilled and unskilled workers will change over time, often with demand for skilled workers rising with technical advance (and therefore normally with GDPPCP) and supply rising slower or faster in different time periods and conditions. The code includes an iterative procedure around the calculation below to assure that the wages of skilled workers are at least 5 percent above those of unskilled workers.
The above initial calculations over time of value added by household type and sector (VADDDHHUi and VADDHHSi) will not be equivalent in aggregate to the household earning share of GDP as indicated in the stylized equations, in part because of the holding of wage patterns across skill and sector to those of the first model year. To assure the needed equivalency in the final calculation (VADDDHHU and VADDHHS), they are normalized within each sector to the labor share of value added from the production function.
The additional term using capacity utilization (CAPUT) in the normalization process shown below will generate some shift in the economic shares between capital and labor from the stylized division related to the Cobb-Douglas exponent parameter. In the code that term is only added to the normalization process when capacity utilization exceeds the target value parameter for it (caputtar). The logic for this is that, when capacity utilization is high, firms will effectively be able to take a larger share of the value added and the household share will be reduced. Also, the impact of capacity utilization is only activated when the economic growth calculation is endogenous, not when the parameter gdprext makes it exogenous.
where
This allows the final calculation of economy-wide household earnings by skill level.
That in turn allows the final calculation of firm earnings as the residual within the value added of each sector and therefore the total GDP.
The earnings of households and firms constitute, however, only a foundation for the SAM, built from the domestic GDP. Transfers to and from other agents, domestic and international, are the SAM’s elaboration on that foundation. Important parts of that elaboration are determining disposable household income (HHINCDIS) and its division between consumption and savings, as well as determining disposable firm income (FIRMINCDIS) and its disposition. (IFs also includes legacy variables named HHINC and FIRMINC, used before the clear separation of earned income and disposable income―these are being phased out with continued model development.) We begin the SAM elaboration with households.
3.3 Households
Households make decisions about the trade-off between consumption and savings and about what to consume based on disposable income, not just earned income. The following subsections first specify the calculation of disposable income and then turn to specification of share (and currency value) of income consumed and what is saved. In general, the forces that affect that division of income into consumption and savings involve two sets of factors: demography and larger economy equilibration dynamics (including those around interest rates and inventory stocks plus related prices).
3.3.1 Disposable Income: Conceptual and Theoretical Foundations
3.3.1.1 From earned to disposable income
Calculating disposable household income (HHINCDIS) involves augmenting or decrementing the earned household income (HHINCEARN) discussed in Section 3.2 by domestic and/or international transfers. The transfers to households from government are social well-being or welfare payments (GOVHHTRNWEL) and pension benefits (GOVHHTRNPEN). The transfers to government are social related payments including those for pension funds (HHGOVSS) and tax payments (HHTAX) plus a share of indirect taxes (INDIRECT) relative to the total earnings of firms and both household types. All government transfers within the SAM are documented in Section 3.4. The transfer from firms is of dividends and interest (HHDIVINT). Households also benefit from or in some cases send remittances across borders and the net inflow (XWORKREMIT) augments disposable income. The default model assumption for remittances is that the share going to unskilled households (ShrUnskilledPop) is equal to the portion of labor supply and population (HHPOP) in unskilled households, an internal variable that dynamically changes across time.
It is also desirable to know the household disposable income per capita (HHINCDISPC), which requires knowing the size of the household population (HHPOP) in each household type (that is, unskilled and skilled). The model assigns total population to households based on the labor supply (LABSUP) in each household type, thereby assuming equal household sizes.
It is important to note that adding an international flow to household income, as well as changing governmental revenues and expenditures in response to international flows including foreign aid and changing firm income in response to foreign investment flows, means that the sum of final demand (C+I+G+X-M) will not precisely equal the sum of value added as it would be in a completely closed economy. While the GDP measured on the output side is definitionally the sum of value added, the sum of final demand with international flows will effectively be Gross National Income (GNI).[4]
3.3.1.2 The permanent income foundation of consumption
Households have ongoing consumption needs and patterns. Thus, when their consumption is examined across years and even life stages it tends not swing as widely as does income when examined across years and life stages. Milton Friedman (1957) originally put forward the “Permanent Income Hypothesis” that consumers link their consumption to lifetime earnings expectations and only slowly change patterns with new developments. Over time the hypothesis gained empirical support and wide acceptance (e.g. Hall 1978; Pistaferri 2001; Shapiro and Slemrod 2003). For that reason, we begin formulating the relationship between income and consumption by computing an internal model variable identified as permanent household income (HHINCDISPERM). The computation uses a weighted average to smooth changes of the permanent income variable in the face of changes in actual annual disposable income (HHINCDIS). The variable itself is advanced by the rate of change in GDP as part of the moving average calculation.
3.3.1.3 Dividing disposable income into consumption and savings: Steps
A critical decision for households (and a very important one for the larger model) is the division of disposable income between household consumption (C) and household savings (HHSAV). Calculation of the share of disposal income spent on consumption (and therefore savings as a residual) has three stages. In the first stage, a preliminary calculation of consumption spending is anchored in each country’s pattern of past years, influenced also by global patterns of consumption across economic development levels, with attention also to savings stocks and needs for them in retirement year (in line with the permanent income hypothesis). In the second stage of calculation consumption is influenced by life-stage specific patterns for dividing income into consumption and savings, in interaction with changing demographic patterns unique to the country. And the third stage recognizes the influence of large-scale equilibrating processes on consumption, namely the market’s society-wide balancing of supply and demand of goods and services (generating signals tied to inventories and prices) and society-wide balancing of savings and investment (with signals via interest rates).
3.3.2 Basic household consumption propensity
The basic initial calculation of household consumption C (indicated as CInitial[5] below) has three steps: (1) calculation of a typical or target propensity for consumption as a share of GDP based on cross-sectional analysis; (2) the calculation of a preliminary country-specific value tied to the permanent household income basis and a consumption ratio (CRA); (3) some very slow convergence of country pattern toward the typical propensity over time.
Concerning a long-term typical or target consumption pattern (CTarget), cross-sectional analysis across societies globally shows that the share of GDP devoted to household consumption varies widely (in the base year from about 30-100 percent), but it tends to decline somewhat with higher levels of GDP per capita and purchasing power parity (GDPPCP). This is consistent with the potential of households with higher incomes and typically longer life spans to save a larger share of income and with the tendency for governmental spending as a share of GDP to similarly rise with socio-economic development and partially push out household consumption. We use a cross-sectionally estimated function of that relationship to calculate a typical and long-term target household consumption propensity (HHCPropen) as a portion of GDP.
where
Two explanations of the above equation are important. First, it computes the long-term target value for consumption as a function of relative price adjusted GDP potential (GDPPOTRPA) rather than GDP. An earlier documentation topic noted the value of that variable, especially for countries with significant trade dependence on raw materials like energy that are subject to substantial price swings. Second, changes in government pension shares of income (PenShrInc), responsive to total government pension transfers to households (GOVHHPENT) over time, can add to consumption potential; this assumes that pensions are mostly consumed.
The second or inertial contribution to the initial estimate of consumption involves calculating a preliminary estimate of household consumption for each of the two household types (ConsumHHPrel) by multiplying a consumption ratio (CRA) as a portion of permanent disposable household income times that income. The consumption ratio is carried along from year-to-year, providing an inertial but changing element of consumption (it is updated each year after finalizing the computation of consumption).
In addition, this is all multiplied by a term (HHSavSurStockMul) that represents the evolving balance (HHSAVSURSTOCK) between the needs of households for savings when older and their accumulated savings. The calculation of the multiplier uses a function named ADJSTR, which Section 4.4.2 explains in the context of market equilibration using a PID controller logic.
The sum of the inertia-based preliminary consumption computation across household types is modified by the change in consumption propensity (HHCPropen) over time and, like the target value, by the changing pension share of income.
Many countries have initial consumption shares of GDP that are especially high or low for a variety of historical reasons (e.g., high receipt of external assistance or remittances can boost C and governmentally-induced savings can reduce it). So there is very slow convergence of C toward the more typical cross-sectional pattern for it, using again the household propensity to consume to drive C very slowly toward the target value (CTarget) in a standard IFs function, ConvergeOverTime.
3.3.3 Other demographic modification of consumption and savings
We have seen above the incorporation into a preliminary calculation of the household consumption variable of the influence of demographics. The attempt at least roughly to balance the stock of household savings with the need for those post retirement age is driven by the age structure as well as by income levels and the propensity to save across different life stages.
In the computation of annual consumption as a flow there is a need to look further at the impact of typical life consumption/savings patterns, We look at how age structure and possible scenarios around extreme needs for changing retirement age affect those patterns.
3.3.3.1 The impact of age structure on consumption
Modigliani (1976) sketched the pattern of life-cycle savings and consumption and many others have followed (e.g. Lee and Miller 1992, Zhang and Zhang 2005, Zhang and Zhang 2009, Lee and Mason 2011). Aggregate consumption as a portion of income tends to be lowest during the peak working years and higher for the young and the old and/or retired.[6]
Drawing especially on Lee and Mason (2011) IFs represents a relationship between propensity to consume and age (the percentage portion of household income that would typically be consumed at different ages). Across several steps we use that to differentiate consumption demands or needs of the population prior to working years (CPREWORK), during working years (CWORKING) and in retirement (CRETIRE).
In a first step an analytical function with age as the independent variable is used to compute an estimate of the percentage of additional income that each of the three groups consumes (YouthCon, WorkerCon, and PensionerCon). The function uses two parameters indicating the normal age of entry into the work force (workageentry) and normal retirement age (workagretire) and also the model’s calculation of life expectancy (LIVEXP) to calculate those three percentages; the three age-defining values can vary across time, country, and scenarios.
3.3.3.2 Potential diversion: The impact of great life expectancy extension
At this point there is a potential diversion from the normal flow of computation of the impact on household consumption of different propensities by age in interaction with changing age structure. The diversion is activated only if the parameter cpctnduse (percent used of needed consumption) has been assigned a value larger than its default 0.0. As of this writing this parameter has only been activated in model analysis around very great extension of life expectancy with associated need for endogenous calculation of a substantial postponement of retirement age (WORKAGERETIREND). If it were used in the future, we would recommend revisiting and testing the structure described below.
The calculation of the needed retirement age in the face of great extension in life expectancy is informed by the annuity formula PV = C * [(1-(1+i)^-n)/i]). The actual calculation is done in a function of the population model named RetirementAgetoPreserveSavingsRate. In that routine the main equation is
where
Given that age of retirement needed when life expectancy is greatly extended, it is possible to calculate SavingsNew, which reflects the calculation of savings rate needed with that much extended retirement age needed to maintain consumption in retirement. SavingsOld reflects savings using the normal parametrically specified retirement age (workageretire). The new and old values are built around the value of 20, the percentage of household income that the functions described earlier as WorkerCon that the analytical function described earlier generated as the basic propensity for percentage of income saved in the working years (100-WorkerCon).
The difference between the needed and parametrically generated savings rates suggests the additional (or lesser) savings percentage needed.
A portion of that (determined by the same optional parameter) can be subtracted from the consumption of workers so that they will instead save more.
3.3.3.3 Finalizing the impact of age structure on consumption
Returning to the flow of computations regardless of the value of cpctnduse, we also compute the share of the three groups in the total population using the size of three groups (POPPREWORK, POPWORKING, and POPRETIRED), also calculated in the population model.
With or without the diversion, it is now possible to complete the calculation of an adjustment factor (AgingAdjustment) that will affect the level of consumption due to current conditions of the country-year related to the distribution of the population across the age structure in interaction with the propensity for consumption at different ages. It also can optionally take into account possible changes that would be needed if a scenario (activated with the parameter cpctnduse) were to call for major adjustment of the retirement age in order to assure adequate financing. Such a scenario would have resulted in a calculation of a needed retirement age different from the one specified normally by the workageretire parameter.
Having values from the population model for distribution of the population across youth, worker, and pensioner categories (YouthPopShr, WorkerPopShr, and PensionerPopShr) and having values for the consumption propensity for those same categories (YouthCon, WorkerCon, and PensionerCon) allows an estimate of the share that each group would have of the total household consumption.
The sum of the consumption shares follows.
The difference between that sum of shares and its value in the base year provides basic information on how the changing age structure of a population across the three groupings will typically affect consumption intensity. Multiplying that by the permanent disposable household income (HHINCDISPERM) suggests whether consumption might likely rise or fall relative to our more inertial estimate of it, and by how much. The AgingAdjustment (normally but not always populations are becoming older so the term is positive) is added to the earlier initial calculation of consumption (CInitial) to obtain a revised value (CRev1). [Note: in the model code C is repeatedly revised and used instead of CInitial, CRev2, … but different names are provided here to make equations and model flow clearer.]
This revised consumption can then be divided among the population-age categories in a normalization process.
3.3.4 Consumption and saving: Equilibrating dynamics
Although the long-term division by households of disposable income between consumption and savings is heavily influenced by life cycle patterns of individuals in interaction with the demographic patterns of the society, households respond also to other dynamics and therefore variables in IFs. These include interest rates and prices of goods and services. The revisions to basic propensity for household consumption as a share of GDP (CRev1) are revised further in IFs (CRev2) by three terms briefly described here, with the equilibration dynamics that compute them elaborated in Section 4.
The first multiplier above (IntrMulTermC) is computed based on variations of interest rates from long-term patterns. Higher interest rates reduce consumption in favor of savings, as well as helping balance savings and investment.
Although the model could use the real prices of goods and services to affect consumption, those prices in IFs are based on the level of inventory stocks compared to the desired level (which also drive price changes). That difference in IFs between actual and desired stocks is captured in a variable representing the surplus or deficit of stocks (ExcessStocks). The recursive structure of the model means that stocks are updated and prices are computed late in the code sequence of each year in the model’s run, after all production and final demand variables are finalized. Hence it is the level of the previous year’s surplus or deficit in stocks that enters the equation above.
The third term above (Mulcon) recognizes that various other adjustments to levels of consumption and savings should still be sensitive to the reality that over the long term, savings rates of countries tend to fall within a quite narrow range. Despite huge variations across countries, World Bank data show that total gross domestic savings as a percentage of GDP averaged globally about 25 percent from 1970-2019, within the range of 23.5-27.5 percent.[7] That is, there is a propensity for total national savings rate values (and therefore gross capital formation) just as there is for consumption. In long-range forecasting there is thus basis for further adjusting household consumption to facilitate movement toward that propensity, using a multiplier (MulCon) that adjusts over time from initial conditions toward a target. Given computational sequence, this multiplier is lagged from the year before as is the excess stocks variable.
Section 4.4.2 explains the equations that generate both multipliers (both of which use the PID logic elaborated more generally in Section 4) and the additive term.
3.3.5 Consumption and investment: Exogenous intervention
The introduction of a scenario to change investment/gross capital formation (IGCF) can be done in IFs using the multiplicative parameter on investment (invm). That parameter varies around its base value of 1.0. An adjustment term (IAdj) is calculated based on the difference between the parameter and 1.0. That adjustment factor is subtracted from consumption, as well as being added to gross capital formation.
3.3.6 Finalizing household consumption and setting propensity for future years
Extreme values of household consumption and gross capital formation can sometimes be generated by poor data fed to the preprocessor or via the model dynamics. The final calculation of household consumption (C) thus bounds it, using values that are hard-coded rather than parameterized. Lower and upper bounds each involve a number of rules. For instance, it on the lower end, C is not allowed to as a share of GDP to be less than 40 percent. On the upper side one bound is the share of GDP and that maximum upside percentage falls from 180 to 140 over 20 years. These limits are very broad and extremely seldom binding. Similarly, gross capital formation (IGCF) is bound at this point to not exceed 40 percent of relative-price-adjusted potential GDP.
Having modified total household consumption (C) in various computational steps, the preliminary household consumptions (ConsumHHPrel) of the different household types are normalized to this final total.
The rates of consumption relative to disposable income (CRA) can then be re-computed and saved for the next year’s use in the preliminary calculations of consumption prior to the various adjustments of C.
The relative rates of consumption as shares of disposal income in unskilled and skilled households is kept constant across time in this process. (And therefore distribution of consumption across household types is driven by the distribution of income across them, which does change both in response to changes in earnings and transfer patterns.) That is not ideal, but IFs uses no alternative formulation at this point. It is therefore also important to explain the initialization of those rates by household type. In the first time-step, those rates are calculated taking into account the differential propensity of populations at different levels of income to consume and save.
The average propensity for the entire population to consume in the initial year (AveConsumR) can be calculated from data, which are available for total countries but not by household type.
If both types of households consumed an equivalent share of income, they would consume at the average rate. Almost certainly, however, lower income, unskilled households have a higher marginal propensity to consume than do skilled households. In the absence of data-based knowledge about that across countries, IFs currently uses a stylistic, and flexibly changeable function to represent the differential consumption propensity of unskilled worker households (ConsumDiffR), assumed to be less in countries with higher income per capita (proxied by GDP/capita at PPP).
The consumption differential from the function adjusts the average rate for unskilled households and allows computation of actual consumption (ConsumHH) of the unskilled households and a residual calculation of consumption for the skilled households (subject to tests for positive sign and reasonable size, not shown below).
The differential propensity to consume is an important feature for scenario analysis, because transfers across household types (and resultant changes in relative disposable income) are one of the key policy levers available to governments for affecting income distribution and poverty levels.
where
This allows then that initial year estimate of consumption propensity that will vary by household type with that variation carrying over across time, even as the rates of consumption for each household type rise and fall together as the national consumption share of household income rises and falls.
3.3.7 Household consumption by sector
Unskilled and skilled households significantly change their sectoral patterns of consumption (CSCHHU and CSCHHS) as their incomes increase. To capture that dynamics, IFs long relied upon a linear expenditure system (LES)—for a description of the LES approach see Taylor (1979: 219-223). Consumption in each sector of origin and household type (CSHH) in the LES depends upon a minimum level of expenditure in each sector (MINEX) and the marginal budget share (MARBD) of each sector in total consumption (C) above the sum of all minimum expenditures—the floor (FLOOR). The marginal budget shares generated Engel curve behavior of decreasing and increasing shares of consumption budget allocation across sectors. IFs computed the parameters for this consumption function during the first time-cycle of the model. A constant of 0.5 in the equation for MINEX represented the Frisch parameter (the marginal utility of income with respect to income) of -2.0. Parameters and calculations were specific to household type.
Although the LES/Engel elasticity approach behaved well in the short- and even medium-run, it was not really developed for very long-term forecasting. As countries move from very low to very high levels of GDP per capita and household consumption there should be generally similar patterns of sectoral consumption shares across countries at similar levels of GDP per capita. Unfortunately, the LES system did not generate that. Moreover, the partial equilibrium models for agriculture and energy generate values for food and energy demand that need to be accommodated for the most part in allocation of total consumption expenditures, but also subject to the limit of total consumption budgets. Further, base year data on household consumption shares across economic sectors and household types are often not very good.
Therefore, the IFs project replaced the LES approach with a more structural one in which:
(1) The food and energy demand values from the respective partial equilibrium models are accommodated insofar as they total less than 95 percent of the consumption budget. If they exceed that, the consumption budget (C) is increased to facilitate 95 percent at the expense of investment/gross capital formation (IGCF).
(2) Cross-sectionally estimated functions for household-type consumption budget shares (CSComp) of other sectors (and those in agriculture and energy if the partial equilibrium models are disconnected with values of 0.0 for agon and/or enon) are computed as a function of disposable household income per capita. In the first year of the model additive shift factors (CSHHShift) are computed to represent the difference between data for the country-sector shares and function-based values. Those shift factors are converged slowly (over 100 years) to 0, thus determining sectoral consumption shares in the long-run with the function-based values.
where
(3) The entire set of sectoral consumption shares is normalized to the total consumption budget of each household type. Because values for CRA have already been computed, any increase in total consumption to accommodate food and energy needs is not carried to future years.
3.3.8 Household savings
Household savings terms (HHSAV) are calculated as residuals for each household type after disposable income and consumption calculations.
3.4 Firms
The agent class that is least extensively developed within IFs in terms of equations and model formulations is that of firms. Economic analysis of firm behavior typically emphasizes profit maximization, just as analysis of households focuses on motivations including income increase and potentially saving for retirement. In IFs, the equilibrating dynamics around savings and investment represent such behavior for both households and firms longer term, as described earlier in this documentation for households and elaborated for both in discussion of savings and investment decisions in equilibrating processes (see Section 4.6).
Here we focus on the immediate accounting structure for firms. Accounts must balance. Firm earnings coming directly from the value added calculated in the production function, subtracting out value added attributed to the labor of unskilled and skilled households (see also in Section 3.2, explaining the bridge from value added to the earnings of households and firms).
That value added is already net also of the purchases by firms of intermediate inputs and therefore serves as the basis for computation of the disposable income of firms (FIRMINCDIS). That disposable income is gross firm earnings minus net transfers to households in the form of dividends and interest payments (HHDIVINT) and to government via various taxes (FIRMTAX) and social system payments (FIRMGOVSS). In IFs, indirect taxes (INDIRECTTAX) are assumed to be paid by both firms and households, so the total amount paid by firms is represented as the firm share of combine firm and household earnings. Firm savings (FIRMSAV) are set equal to that disposable income.
where
The earlier discussion of government revenues showed the computation of the taxes levied on firms (and households). But we have not explained the computation of the dividend and interest transfer payment to households used in the above equation and how that is split between the two types of households. A foundational step for that is to compute firm income after taxes but before such distributions to households (FirmIncomeAfterTaxes).
IFs computes in the first year a firm investment ratio to that after-tax income (FirmInvRI) as a very rough indicator of the portion of firm income after taxes that is used for gross capital formation. The residual after capital formation (investment) is the portion that can be passed back to households as dividends and interest. In the absence of data on the distribution of dividends and interests between unskilled and skilled labor-based households, equations arbitrarily assign the overwhelming share of it, namely 90 percent, to skilled households.
where
Again, these equations represent the accounting at any given time point. Section 4 of this documentation will move to discussion of intertemporal dynamics and equilibrium-seeking across time. First, however, we need to understand some of the accounting interactions of households, governments, and firms internationally.
[1] As a graduate student in what is now the Josef Korbel School of International Studies, Anwar Hossain worked with Barry Hughes in the development of the SAM structure and database for IFs (see Hughes and Hossain 2003).
[2] https://www.oecd.org/sti/ind/input-outputtables.htm
[3] https://www.oecd.org/sti/ind/input-outputtables.htm
[4] For GDP, GNP, and GNI definitions see https://www.economicshelp.org/blog/3491/economics/difference-between-gnp-gdp-and-gni/
[5] In the IFs code it is common to simply recompute a variable like C without renaming it and there is no new variable named CInitial in the code. In this documentation we sometimes use new variable names to simplify the understanding of a variable that the code changes in stages.
[6] See also https://www.bls.gov/cex/research_papers/pdf/ws2018-marginal-propensity-to-consume.pdf slides 33-35; https://www.aeaweb.org › conference › retrieve; last figure in https://www.researchgate.net/publication/321054696_The_distribution_of_wealth_and_the_marginal_propensity_to_consume/figures?lo=1; Figure 5 in https://www.bls.gov/cex/research_papers/pdf/ws2018-marginal-propensity-to-consume.pdf.
[7] https://data.worldbank.org/indicator/NY.GDS.TOTL.ZS. See also https://www.theglobaleconomy.com/rankings/capital_investment/ showing that in 2019 average IGCF/GDP was 24.52 percent; globally total savings and gross capital formation need to be nearly equal.
3.5 Government
Understanding government finance requires attention to revenues and expenditures, the topics of the first two following sub-sections. It also requires attention to the annual imbalance of those in nearly all countries, the resulting debt or asset stock changes over time, and the feedbacks from those stocks to changes in revenue and expenditure streams. Those equilibrating feedbacks within government finance are treated in the next major documentation section, along with the more general discussion of equilibrations within the economic model. There is also separate IFs project documentation on government finance with updating processes that keep in largely but not always totally in synch with this document.[1]
Also, government finance in many countries, especially in federal systems, involves both central government and subunit governments (provinces, states, districts, etc.). As discussed in a subsection here, the IFs team has put in place some placeholder variables for distinctions between central and more local government finance. The model currently is, however, focused on total government.
Data on government finance are often complicated, in part because of the distinction between central and total government. Supplemental Appendix A reviews the data used in the preprocessor to initialize the forecasting of total government finance.
3.5.1 Government revenue
3.5.1.1 The core calculations of government revenue
The model represents five domestic revenue streams from taxes on household earnings (HHIINCEARN) and on firm earnings (FIRMEARN), which are the labor and capital shares of value added, respectively. A sixth revenue stream is tax (tariffs) on imports (MS). The six streams are: household income taxes (HHTAX), household social security/welfare taxes (HHGOVSS), firm income taxes (FIRMTAX), firm social security/welfare taxes (FIRMGOVSS), indirect taxes (INDIRECTTAX), and tariff revenues (MTARRIFREV). We have no database to distinguish social security/welfare taxes assessed on households and firms, so the tax rate is the same on both (SSWELTAXR). In each revenue equation there are exogenous multipliers that the user can manipulate to simulate changes in source-specific revenue streams (hhtaxrm, etc.) and total government revenues (govrevm). In addition, there is a multiplier on revenues (MulRev) the calculation of which is documented in the separate section on equilibrations in IFs (this one using government debt levels to maintain some reasonable balance of revenues and expenditures, with application lagging one year behind the calculation). As we shall see in the next sub-section, most of the tax rates below are subject to adjustment across time with changing levels of informality; the exception is tariffs where informality does not change the rate, but the multiplier (mtarifftaxrm) does.
where
Some governments also have net domestic revenues from state-owned enterprises, but the model does not represent that stream (which is, in any case, often actually negative).
Total domestic government revenues, before consideration of external revenues in the form of foreign aid (GOVREVDOM) is computed from the multiple revenue streams, after summing the social security or welfare taxes across households and firms (SSWELTAX).
It is useful also to compute the overall tax rate as an output indicator, as a portion of potential, relative-price-adjusted GDP.
For scenario analysis is possible to specify exogenously an overriding value for the total tax rate (and the revenues calculated above) as a target percentage (govrevtrgtval) of potential, relative-price-adjusted GDP (GDPPOTRPA), to be reached over a period of target years from the first (govrevtrgtyr). When target years has a value greater than 1 and the target rate exceeds that generated by the sum of the initial tax calculations (above), the values of taxes collected are normalized to the total target rate level. Given the various exogenous interventions possible and given that the endogenous multiplier to address imbalances with expenditures could be large, limits of 90 percent are placed on taxes as a portion of firm and household earnings.
The domestic revenues calculated above need to be supplemented by foreign aid receipts and net transfers from intergovernmental organizations when either or both are relevant. For aid recipients only, the amount of government receipts adjusts government revenues.
if AIDr >0 then
A final adjustment for government revenues adds possible net loan and credit financial inflows from the World Bank (XWBLNFIN) and the IMF (XIMFCRFIN).
There are no dynamics yet in place for local government expenditures (GOVREVLOCAL). The model now has placeholder variables for net revenue transfers to local governments from central ones (GOVREVLOCALFRCEN) and the direct imposition of taxes at the local level (GOVREVLOCALTAX), but they are now set at 0.0 because they are not yet supported by data in the model and no computations drive or use them. See additional detail on local and central government finance in the subsequent documentation section about them.
3.5.1.2 The impact of informality on tax rates and revenues
The general logic for computing the impact on productivity and therefore GDP from changes in the informal economy’s share of GDP (see Section 2.7.4) is also used for computing its impact on government revenues. The simplifying assumption we make is that informal economies contribute very little or nothing to the true base for household (HHTAX), firm (FIRMTAX), and indirect (INDERECTTAX) taxes and contributions to social welfare programs or pensions (SSWELTAX). Thus, the tax rates (coming to us along with tax bases and amounts from official data) are associated with the formal sub-portion of the official economy and associated tax bases in that official economy. As the share of the informal economy decreases, however, we can expect those bases to expand and to generate effectively higher effective tax rates (FIRMTAXR, HHTAXR, INDIRECTTAXR, and SSWELTAXR) or, if informality increases, to reduce tax rates.
In IFs, we can use this general understanding to increase (or decrease) the effective tax rates accordingly, as the informal economy share of the economy decreases (or increases) relative to its expected value at any given level of GDP per capita. That is, we operationalize the informality impact on tax rates in terms of changes from the first model year in the excess or surplus of informality share (ExDefInfGDP) relative to that expected value.[2]
Specifically, we compute a tax rate adjustment factor (TaxInfAdjustmentFac) that reflects this change in the domestic tax terms, also introducing a multiplicative parameter usable for scenario analyses (taxinfadjm).
Because the adjustment factor is computed relative to the first year (t=1), the change in all four tax rates are also applied to the rates of the first year. (In the case of households there are two rates (h), for skilled and unskilled households.)
Total government revenues are responsive primarily to these tax rates and their bases and the model includes dynamics that link government expenditures to the taxes and fiscal balances. Thus, changes in these revenues have pervasive effects through the rest of the model.
3.5.2 Government expenditure
Government expenditures (GOVEXP) involve (1) transfers to other agent categories (households, firms, and other countries, of which IFs only represents those to households (GOVHHTRN) and other countries via aid (AID) and (2) direct consumption (GOVCON). There are no dynamics yet in place within IFs to separately compute values for the variable local government expenditures (GOVEXPLOCAL), so the focus is on expenditures of the total government. The two components of total expenditure each require a moderately complex calculation. We begin with attention to transfers to households, then turn to total government consumption, followed by explanation of the division of total consumption into destination sectors (GDS) or subcategories (such as military expenditures, health, education, infrastructure and R&D). A later section of this documentation deals with AID outflows.
More than a century ago, the German economist Adolph Wagner (1835–1917) identified the propensity for governments to increase the share of the economy they collect and use over time (Wagner 1892), a pattern that has come to be known as Wagner’s Law. Consistent with this, the government expenditure share in OECD countries grew from around 10 percent of GDP in 1870 (World Bank 1997: 2) to a relatively stable 40–45 percent between 1991 and 2015 (IFs calculations using IMF data). Non-OECD countries exhibit similar but more recent patterns of growth. Within the total expenditure picture there are different patterns for direct consumption expenditures (such as those on the military, education, health, and infrastructure) and transfer payments. Global general government direct consumption expenditures (without transfer payments) have climbed since 1960 as a portion of GDP to about 14 to 18 percent (IFs calculations using WDI data). Transfer payments have climbed more rapidly and now exceed direct expenditures globally. Because of this tendency for government finance to grow as a percentage of the economy, the equations in IFs for transfers and direct consumption expenditures include a Wagner tern with a coefficient that builds in increasing rates over time. As the model has evolved, however, such growth has increasingly become endogenous (driven largely by the demand for increased expenditures) and in recent model versions the coefficient has been given a default value of zero; it remains useful for scenario analysis.
3.5.2.1 Government to household transfers
Within a social accounting matrix, government transfers can go to either households or firms (most often as subsidies). IFs explicitly represents only those to households, although the setting of the firm tax rate could be used in scenarios to conceptualize net flows to firms and therefore also subsidies. The transfers to households are divided into two categories, pension support for the elderly (GOVHHPENT) and social (or welfare) transfers (GOVHHTRNWEL).
The total value of government transfers is computed using two different behavioral logics, a top-down one like the one described above for government consumption, and a bottom-up logic. The bottom-up logic is especially important in the analysis of pensions, because it is responsive to the changing size of the elderly population. After explaining the two logics we will turn to their reconciliation.
Top-down household transfer calculations. The top-down logic uses an aggregate function responsive to changes in GDP per capita at PPP to calculate an estimated value of transfers as a portion of total government expenditures (EstGovtHHTrnPortion).
The estimated value for the portion of total expenditures that household transfers constitute, adjusted by an initial shift term to accommodate initial data (GovHHTrnR), converges over time (govfinconv) to the estimated value without the shift term.
where
The initial calculation of the portion of GDP that will be devoted to transfer payments is adjusted by a Wagner term to represent possible growth with time (noted above to now being used only in scenario analysis). The result (converted from percentage to ratio) is multiplied by an adjusted calculation of GDP (GDPBase). The adjustment moves the GDP half way to the value of relative-price-adjusted GDP (GDPRPA) in order to push through some of the potential implications of changing trade prices, especially relevant for oil exporting countries where GDPRPA can swing quite a ways from GDP with changes in oil prices. Finally, the calculation is affected by an exogenous multiplier for scenario analysis (govexpm) and an endogenously computed multiplier term to adjust government revenues and expenditures to each other over time, with a lag (MulExp). Section 4 explains this multiplier in the context of model-wide equilibration processes.
where
Finally, there are adjustments to reflect the possible impact of changing financial flows from foreign aid (AID)―changes, because the base year’s foreign aid is already built into the data for government transfers. IFs assumes that governmental use of foreign aid receipts is split between a portion going to transfers (GovHHTrnPortion) and a portion going to direct consumption (GovConPortion), the split determined by a parameter (aidrecgovconp).
where if
Bottom-up household pension calculations. Unlike the single term in the top-down logic, the bottom-up logic involves computing two terms, one for pensions and one for social welfare, in preparation for summing them and reconciling the sum with the top-down calculation.
Bottom-up pension calculation.
The bottom-up pension calculation itself is done in two ways. The first is driven heavily by a function of GDP per capita. The second is driven heavily by the size of the retired population and its pension needs.
Bottom-up pension calculation from GDP per capita. The bottom-up pension term, like the top-down logic, begins with an initial estimate of pension expenditures (GovtPensionRateFromGDPPC) as a portion of GDP using a function estimated cross-sectionally with GDP per capita at PPP. Not shown is an algorithm that then ramps up that estimated portion from 1 percent to 8 percent as GDP per capita at PPP climbs from 0 to $8,000, over-riding the bottom portion of the analytical function.
An initial estimate of total government pension spending (GovtPensionsFromGDPPC) is calculated by multiplying this rate estimate, adjusted for the shift (GovHHTrnPenR) between estimate and actual value in the first year, by the potential relative price adjusted GDP (GDPPotRPA).
where
Bottom-up pension calculation from retired population size and needs. Consistent with the bottom-up logic, that initial calculation is compared with a calculation that is built up from an estimate of the financial needs/demands of retired population. That second estimate starts with the size of the retired population (RetirementPop), modified if the age of retirement has changed in scenario assumptions (labretagem). It multiplies that by the pension per retiree calculated in the first year (GovHHPenPCI), scaled upward by the increase in relative-price-adjusted potential GDP per capita (GDPPotRPAPC) since the first year.
where
Bottom-up pension calculation finalization. The simple average of the two estimates for bottom-up calculation of pension needs becomes the bottom-up calculation of pension needs.
A further algorithmic check is made of the above calculation to limit per-person pension requirements as the size of the retired population grows from below 20 percent of the total population (in which case the limit is the average per capita GDP) to 40 percent or more of the total population (in which case the limit is 70 percent of the average per capita GDP).
Bottom-up household welfare transfer calculations. The bottom-up calculation of welfare transfers has similarities to that for pensions. It is, however responsive to the total population (POP) rather than the retirement age population. And rather than relying on a cross-sectionally estimated pension level, it more directly scales up initial welfare transfers per capita with change across time in the in relative-price-adjusted potential GDP per capita (GDPPotRPAPC).
where
Total bottom-up pension and welfare transfers. The total bottom-up transfer calculation is the sum of those for pension and welfare transfers.
Reconciling top-down and bottom-up calculations. The larger of the two numbers indicates the total pressure in the system for transfers to households, not to exceed 50 percent of potential relative-price-adjusted GDP.
Given these total transfers, there are further steps required to finalize the division into pension and welfare transfers and to divide each of those into transfers to skilled and unskilled households. The first step is an interim division of the total into pension and welfare categories using the bottom-up calculations.
Allocating pensions to skilled and unskilled households and optionally adjusting levels. The split to unskilled and skilled households is proportional to the share of their respective earned incomes in total household earnings (HHINCEARN). An exogenous multiplier (govhhtrnpenm) can alter government pension transfers, causing the sum across household types to exceed or fall short of the original total calculation, so a new total is computed (GOVHHPENT).
A further adjustment to the pensions for both household categories is possible but not made except in scenarios. If the value of govhhpentndpctuse is greater than 0 (it is 0 in the Base Case) and CRETIRE (the consumption of retirees in the previous year) exceeds 1% of GDP and is therefore of some interest, then two modifying terms are computed that help adjust government pension levels toward those needed to satisfy retirement income needs. The first is a value by which pensions might fall short of needs or be in surplus (PensionShortSurp) based on an annuity calculation that looks at a needed retirement age for adequate consumption potential calculated in the population model (WORKAGERETIREND) and the age of retirement specified exogenously in any IFs model run (workageretire). The value for PensionShortSurp is allocated to household types based on their relative share of total household pension receipts.
The second is a pension multiplier (MulPension) that is modified over time from an initial value of 1 and used to increase or decrease government pension transfers to households (GOVHHTRNPEN) as augmented by the first term. If in the preceding year the consumption needs of retirees (HHRETIRENEED) exceeded the consumption spending levels of retires (CRETIRE)―both variables are filled in the household calculations of the SAM, then the multiplier is somewhat increased on the presumption that governments will try to fill the shortfall.
where
Pension transfers are bounded to be below 25 percent of GDP.
Allocating welfare transfers to skilled and unskilled households.
The initial calculation of welfare transfers is split between household types based on their relative population (HHPOP). An exogenous multiplier (govhhtrnwelm) can change the value of those transfers. The welfare amounts are further adjusted if net flows for categories 3 and 4 (targeted at unskilled and skilled households, respectively) from international financial institutions (XWBFLOWS) have changed from initial conditions; those are added to the welfare transfers. Welfare transfers are bounded to be below 37 percent of GDP.
One last change of welfare transfers to unskilled households involves possible flows from a hypothetical potential and by default non-existent global fund (GlobalFund) to countries based on income/consumption shortfalls from poverty targets at different levels (e.g. PovShortShare) and an exogenous parameter (globalfundsrecipients). The size of the global fund is tied to levies on trade and the fund is only created when the bilateral trade option is turned on (by default it is off). When the fund has a positive value and for countries with a positive value of the parameter, welfare transfers to those countries are increased by a share of the fund determined by the poverty shortfall and the parameter.
Final calculation of government transfers to households. Given that both pension and welfare transfers are potentially modified from initial calculations in the steps outlined above, the total transfers from governments to households is recalculated.
3.5.2.2 Total government consumption
Computation of government consumption or GOVCON (direct expenditures on the military, education, health, R&D, foreign aid, and other categories) begins with use of a function to compute estimated government consumption (EstGovtConsumPortion) as a portion of GDP, using GDP per capita (PPP) as the driver. The function supports a behavioral assumption of generally increasing expenditure ratios with increases in GDP per capita. The rate of increase is very slow, however, and the percentage of direct government consumption in GDP (as opposed to transfers) in most countries is between 15 and 25% of GDP.
The estimated value then enters a convergence calculation to calculate an initial value for GovConPortion, the portion of GDP that government consumption constitutes. In the first year a shift factor (GovConR) is computed that represents the degree to which a country’s base year consumption/GDP differs from the estimated value. That ratio multiplies the estimated term in future years, allowing the function normally to increase consumption/GDP as GDP per capita rises. At the same time, such divergence from estimated functions is almost as often a matter of data inadequacy or of temporary factors for a country as it is of persistent idiosyncrasy. The convergence function allows the country/region’s value to converge towards the functional calculation over a period of time (govfinconv), usually quite long. Such convergence also helps avoid ceiling effects (e.g. government consumption as 100% of GDP) as GDP per capita rises.
where
The initial calculation of the portion of GDP that government consumption constitutes is adjusted by several additional terms and then multiplied by a GDP base (GDPBase) to obtain the basic calculation of GOVCON. The first adjustment term in the equation below is called the Wagner term, after the discoverer of the long-term behavioral tendency for government expenditure to rise as a share of GDP. This is built into the consumption calculation through an exogenous parameter (wagnerc) that is multiplied by the number of the forecast year. The use of the Wagner term is a legacy representation in IFs because the use now of the cross-sectional function provides an empirical basis for the growth in GDP share by government consumption. Thus, at the time of this writing the coefficient’s value was 0. It can still serve as a scenario parameter.
The second and third multipliers are used also for government transfer payments. Thus, an exogenous multiplier of government expenditures (govexpm) allows the user to directly control both direct government consumption and transfer payments by country/region. A second exogenous multiplier (govconm) allows directly control of only the consumption portion of government expenditures. Finally, an endogenously computed multiplier on expenditures (MulExp), parallel to a multiplier on revenues (MulRev), reacts to the balance or imbalance in government expenditures and the debt level (see the discussion of equilibration of revenues and expenditures for detail on computation of both in subsequent Section 4.4).
The resulting adjusted value of government consumption portion of GDP is divided by 100 and multiplied by a GDPBase term. The GDP base term could just be GDP. But relative price adjustments in countries can greatly affect government consumption—for instance, rising and falling relative oil prices can sharply affect government revenues and expenditures in oil-rich countries like those of the Gulf. Hence, we arbitrarily add half of the difference between the GDP relative price adjusted value (GDPRPA) and the GDP to the base from which we compute the basic and near final value of GOVCON (GOVCONBase).
where
Finally, there are adjustments to reflect the possible impact of financial flows from international financial institutions (IFIs) such as the World Bank or International Monetary Fund (called XWBFLOWS independent of the source) and from foreign aid (AID). Because we assume that such flows are already in the base year data values for total government revenues and consumption, the IFI term represents the absolute difference between those flows in the current and initial years. The targets of those IFI flows are set exogenously via a parameter (xwbsectar) that is dimensioned by target of flow (ft), namely (1) education, (2) health, (3) unskilled households, (4) skilled households, and (5) other. Funds for the first two targets go to government consumption and funds for the household targets go to transfer payments. Extensive documentation of the stocks and flows associated with IFI funds and the user control of them is provided elsewhere in economic model documentation. The aid flow term similarly represents the difference between current and initial net receipts, allocating a portion (aidrecgovconp) of this to government consumption (the rest goes to household transfers).
where
As an alternative to the structure described above, the project has experimented with the computation of GOVCON not from a single function, but as the sum of estimates of its various destination components such as military and education (the GDS vector discussed later), with each of those estimates computed as a function of GDP per capita). That is rather more complex than necessary.
3.5.3 Government consumption by origin sector
The division of government consumption expenditures into target destination categories (GDS), part of the broader socio-political module of IFs is described in the next subsection. That division is, of course, also a key agent-class behavior. With respect to sector of origin for government consumption (GS), which is information needed for the equilibration mechanism in the core commodities module, IFs simplistically assumes in the preprocessor (because of an absence of data or even good qualitative information) that all government spending except arms, which has its source in manufactures, comes from services. On a year-to-year basis, the sectors of origin of GOVCON remain fixed at the initial proportions.
3.5.4 Government consumption by destination use
As indicated, government expenditures in IFs fall into two categories: transfers (GOVHHTRN) and direct consumption (GOVCON). Direct consumption expenditures fall into the following subcategories: military, health, education, research and development, infrastructure (the core types elaborated in the infrastructure model), other infrastructure (all non-specified infrastructure types), and other (including administrative outlays and implicitly foreign aid given by donor countries). IFs divides total government consumption (GOVCON) into these destination sectors (GDS) in the process described below. The user can change that default pattern of government spending over time with a multiplier parameter (gdsm). The model normalizes the destimation allocation to total government consumption.
Several issues that complicate the calculation of GDS and assuring that the sum of it across all categories equals GOVCON. These issues are:
- In the cases of education, health, and core (model elaborated) types of infrastructure, IFs contains models that produce calculations of expenditure needs or demands. Attempts to satisfy these demands in whole or part require adjustments in GDS for other spending categories.
- In the cases of health, infrastructure and R&D categories, the model represents private as well as public spending (it should eventually also do this for education but does not at this time). These private expenditures need tracking also and can, as in health, affect the ability of the government to meet total bottom-up cost demands.
- In the case of military spending, the model uses an action-reaction formulation that links spending of some countries to that of others (see the documentation of international politics). This is the reason that IFs code for GDS calculation was initially placed into and sits in the international political model.
- In the case of education and health, financial flows into or out of countries from international financial institutions (IFIs) such as the World Bank need to adjust the values of GDS.
One strategy for attacking these complications is that same one that is used in IFs for addressing complications around government transfers to households, namely the use of top-down and bottom-up calculations of government consumption by destination category and then their reconciliation with each other and total government consumption. The key difference with respect to government consumption, however, is that top-down calculations for the consumption categories not elaborated in models of their own (namely military, R&D, other infrastructure, and other) are carried forward directly to final calculations without their being any bottom-up calculation of them. In sharp contrast, the top-down calculations for education and health are compared with subsequent bottom-up calculations and the final calculation is a weighted average. Also, in the case of core (elaborated) infrastructure, the complexity of its categories led to the decision not to compute a top-down calculation, only a bottom-up one.
3.5.4.1 Top-down GDS calculations
Although very much a part of the SAM structure and therefore tied to economic modeling, the code determining government spending by category (GDS) is situated in an IFs model called sociopolitical (SOCIOPOL.BAS). The first stage in the computation of GDS is the computation of a ratio of government spending in each category to GDP (Gk). In the sequencing of the code, in both first and subsequent years the first steps of that stage are the use of cross-sectionally estimated analytical functions that compute expected military, education, health and other infrastructure expenditures as a percent of GDP (GkComp) as a function of GDP per capita at PPP. A similar analytical function is used to compute total (public and private) R&D expenditures.
In the first model year there are data on such expenditures provided from the preprocessor, so a country-specific, multiplicative "shift" vector is computed (GkRI) that saves the ratios of the actual values to those computed in the functions. In the subsequent years, the values in that shift vector converge to 1 over 200 years, meaning that the pattern generated by the expected values from the functions very gradually take over from the pattern in the initial conditions.
There is no function or process to compute an expected value for infrastructure spending as a portion of GDP per capita. The scarcity of data on total infrastructure spending led model developers to conclude that it was better to use only bottom-up information on infrastructure costs and expenditures.
In the first year the size of the “other” category is available only as a residual from the data values or estimates of public consumption expenditure in all other categories (the preprocessor keeps it from going to zero or negative) and the ratio of that value to GDP (Gk) is maintained as the expected value over time.
More generally, top-down calculations for most categories of government spending (g) take this basic form, in which a shift factor (GkRI)―the ratio in the first year between the initialized share of spending as a share of GDP to the function-based value (GKComp)―converges toward 1.0 over a very long horizon, meaning that gradually the function-based value becomes determinate of the share of GDP being directed to the consumption expenditure (Gk)
where
The product of computed share of GDP directed to each spending category and GDP then provide the top-down estimate of consumption by destination sector (GDS).
There are some variations or adjustments to this general approach by spending category. For military spending the estimate uses the Gk variable, but modifies it by both an exogenous multiplier (gdsm) and a multiplier for military spending (GkMul) computed in the action-reaction process around that spending (described in documentation of the international political model).
For health and education the equation is the largely the same, except for the exogenous multiplier. That multiplier is used only later in the process, when the top-down GDS estimate is being reconciled with the bottom-up cost calculation from the health and education models. Also the flows from international institutions to health and education (XWBFLOWS) are added.
where
The process is slightly more complicated for R&D because of the need to account for both private and public expenditures. The code first computes each year a ratio of the expected share of public expenditures within GDP relative to the first year, a term that will be used as a multiplier in the next step (RandDMul).
That term is used to adjust the initial ratio of public R&D expenditures as a portion of GDP (RandDI) in order to compute the current time step's value, which is allowed to converge, but at minimal speed (1000 years) to the estimated value for the current time step:
where
Finally, this allows the computation of the top-down estimate of GDS for public R&D, exogenously modified with a multiplier (gdsm):
Total R&D expenditures (RANDDEXP) are inclusive of public expenditures and are also computed top-down via an analytical function with GDP per capita at PPP (as PredRandD), subject to an additive shift factor (RandDExpShr). Because the ultimate normalization process will change the public portion (GDS) of total R&D expenditure (RANDDEXP), the values of RANDDEXP and GDS are used to remove the public expenditures (RandDPrivatePercent). After GDS for R&D is recalculated with normalization of all GDS values to total government consumption, the revised version of GDS for R&D will be added back into the total.
where (as a percentage of GDP)
Turning to other infrastructure, the calculation of GDS does not use a modifiable analytical function, but rather a hard-coded one. That function is modified by a multiplicative shift factor tied to the difference between the value produced by the function in the first year and the initial condition for GDS, other infrastructure. The shift factor converges to 1.0 over a long time horizon.
where
At this point, top-down estimates of GDS are available for all government spending categories except core infrastructure (for which no top-down value is computed) and other/residual government consumption (for which it remains set at the initial year’s share of GDP).
3.5.4.2 Bottom-up demand calculations
Bottom-up calculations are made only for the government consumption spending categories corresponding to extended models of them: health, education, and core/elaborated infrastructure. The last of these has no top-down calculation.
We begin with health. The bottom-up calculation of total health cost (HLCOST) has four additive components computed within the health model (POPULAT.BAS code): the first one is due to mortality (HLCOSTMORT), the second one is due to morbidity (HLCOSTMORB), the third one is related to life extension therapy (HLCOSTLE), and the fourth involves other costs such as administrative and legal (HLCOSTOTHER). The first two are specified for each morbidity/mortality type (d) before summing. The third is general and included largely for scenario purposes. The fourth is also general and is computed initially as a residual, given data on public (GDS) and private (HLEXPENDPRIV) health expenditures, minus the base year total of morbidity and mortality expenditures (in the base year the scenario-related expenditures on life extension are zero). All elements of costs are computed in billion dollars.
Within government finance, the bottom-up demand calculation lags a year behind its reconciliation with top-down, so the initial GDP growth rate (igdpr) is used to estimate the growth rate (HlGrTerm) from the previous year’s total cost calculated in the health model. That value is given the most weight, but is averaged with the rate of growth of costs calculated from values in the health model over the last two years.
Within the health model itself, a calculation is made of the share of total costs that are private (PrivExpToCost).
At this point, the actual bottom-up demand for public health expenditures (HlExpDemand) can be calculated from the past year’s cost, estimated growth, and the share which is public as opposed to private.
Turning to education, the basic logic of that cost calculation is that in the first year of the forecast a ratio (EdCostGDSEdRI) is calculated of the public expenditures on education (GDS from data and the preprocessor) and a variable from the education model representing bottom-up costs (EDTOTCOST). A modeling decision was made to make this ratio converge to 1.1 over time, to leave fiscal headroom for pre-primary and other education not associated with the standard levels represented in IFs.
The bottom-up educational expenditure demand (EdExpDemand) used in the budget reconciliation process below is calculated as the bottom-up calculation in the preceding year times this ratio. In addition, a small adjustment is made to the bottom-up calculation from the previous year to make it grow somewhat over time; the initial growth rate is set equal to the initial growth rate of GDP (igdpgr) and allowed to converge to 0 over time.
where
For core infrastructure the value of GDS comes completely bottom-up from a coded function (CalcInfraBudgetDemand) that adds up the public portions of the new construction and maintenance costs for various types of infrastructure for the current year as already calculated in the infrastructure model (and explained in documentation of that model). Given weakness in data availability for infrastructure spending, infrastructure GDS calculations, unlike those in other GDS categories, do not use any reference to either initial values of infrastructure spending or any expected value relative to GDP per capita at PPP.
where
In the equations above, infct stands for the index number of various infrastructure types included in the IFs model, for example, road, electricity, water connections etc.; INFRAINVESTNEW and INFRAINVESTMAINT are total costs of new construction and maintenance respectively and infrainvnewpubshrm and infrainvmaintpubshem are parameters set to represent shares of the costs borne by the government as opposed to the private sector.
3.5.4.3 Reconciling top-down and bottom-up expenditures
At this point the initial top-down or function-based values of GDS have been calculated for military, health, education, R&D, other infrastructure and other government consumption; bottom-up cost calculations have been made for for health, education, and core infrastructure. The calculations of both top-down and bottom-up values for health and education require that we reconcile them.
The process uses a parameter (gdsbudgetprotec) for weighting the bottom-up, demand-side budget need calculations (HlExpDemand and EdExpDemand) relative to the top-down or analytical function-based values (GDS). That parameter takes values between 0 and 1 and provides a weighted average of the two terms. The parameter is dimensioned across all expenditure categories, but the code is only structured to use it in the cases of health and education.
There is a direct multiplier (gdsm) that can at this point be applied to the calculations of GDS for the spending categories that have extended modeling of them. The default value for the parameter is 1.0. Earlier steps for computing GDS for expenditures on the military and on R&D already have applied the same multiplier.
At this point in the program flow logic, there is a test to see the value of a normalization logic parameter (gdsnormalize), the default value of which is 1. Should it be 0.0, recalculations of GDS cease and there would be no attempt to compare the sum of them with the value of GOVCON. Fundamentally, this means that spending-category specific logic would prevail. But it would also mean that the constraint of government revenue-expenditure balancing that earlier determined the value of GOVCON would be over-ridden. Since doing so breaks the accounting logic of the social accounting matrix structure, changing the parameter is not recommended; its existence is primarily for use in model analysis, to see what the spending-category logics generate. The next sub-section assumes that the parameter and the constraints of GOVCON are active.
3.5.4.4 Reconciling expenditures with total government consumption
Two tasks remain to finalize values of government consumption by category:
- Facilitating the optional use of target values for expenditures as a percentage of GDP and the year in which those percentages are reached.
- Normalizing the total of expenditures across categories to the total government consumption (GOVCON) available, simultaneously insofar as possible protecting the specification of percentages of GDP directed to each category.
The first step is the calculation of the sum of GDS at this point in the code flow (GTot) and the comparison of that with GOVCON.
If GTot is larger than GOVCON, then there is a funding constraint and addressing that is required. A parameter to relax that constraint exists (govconswing). Its default value is 0.0 and it would, as with gdsnormalize, be very unusual to change that. This change with govconswing, however, would not disrupt the maintenance of consistency in accounting, because subsequent normalization still maintains the linkage of GOVCON with the sum of GDS values.
More commonly the typical approach if GOVCON is unable to cover the demands posed by the sum of GDS (GTot) is to reduce values of GDS. In that process of reduction (normalization of GDS total to GOVCON), there are, however, protections of two kinds. First, there is some protection of the GDS for spending categories subject to scenario-specified spending as a portion of GDP. A scenario-based specification of expenditures as a portion of GDP is controlled by two parameters, the first specifying a non-zero value for such expenditures (gdstrgtval) and the second (gdstrgtyr) indicating the number of years subsequent to the first model year over which the target value will be reached. Second, there is again some protection of spending in categories for which the budget protection parameter (gdsbudgetprotect) has a non-zero value. Both protections use the calculation of an internal set-aside value for GDS (GDSSetAside).
If then
The TimeFunction (a block of code in the flow of that being discussed here) interpolates from rates of GDS/GDP in the first year to the value of gdstrgtval across gdstrgtyr years.
If then and then
If neither branch is taken, the value of SetAside becomes 0.0. Also, if there is no budget constraint (GTOT is not greater than GOVCON), the value of SetAside is set as GDS.
To summarize to this point, the control logics have been: (1) gdsm (default is 1); (2) how much of each bottom-up values for health and education to protect with gdsbudgetprotec (the defaults are roughly 50%); (3) target percent of GDP and year to reach it (default is not to use); (4) whether or not to normalize (default is yes)
The final steps are the actual normalization. They begin with calculations of the total sum of set-asides, the unprotected portion of GTOT, and the amount of GOVCON left over (reduced) after covering the total of all set asides. In addition, by spending category there is a potential portion of GDS left or unprotected after the set aside.
If there is a positive value for the unprotected GTOT, it is possible to use the category-specific unprotected GDS values as a share of unprotected GTOT to allocate across all expenditure categories the residual value of GOVCON after reduction by set asides (the computation of GOVCONReduced assured that it is non-negative).
If there is not a positive value for the unprotected GTOT, then the set asides cannot be protected and a regular normalization of GDS values to the total of GOVCON can be done across all expenditure categories.
At this point, the sum of GDS values across all expenditure categories will equal GOVCON, as well as extensively protecting bottom-up calculations from the health, education, and infrastructure models and allowing a wide range of scenario interventions.
3.5.4.5 Linking public and private expenditures
At this point it is possible to compute total health expenditures as a sum of government spending and private spending.
It is also possible to add the private R&D expenditure rate back into the variable RANDEXP (the percentage of GDP constituted by the total of private and public expenditures) from which it had earlier been removed.
3.5.4.6 Forward impacts of public expenditure
There are several forward linkages from GDS that are important elsewhere in the model. The most important of these are linkages to multifactor productivity from human capital. Those are discussed in Section 2 of this documentation.
Here we note only two forward linkages, both of which are set up in the same section of code as the computation of GDS. The first is of a mortality multiplier (MORTMG) that is computed for the demographic model, using changes in health spending as a portion of GDP from the initial year and a parameter of the impact of change in that spending rate (elashc).
The second forward linkage at this point is in the calculation of a saved value of health expenditures as a portion of GDP to be used in the calculation of water and sanitation in the infrastructure model. In code around the formulation below, if the exogenous multiplier gdsm for health spending is greater than or equal to 1 (the default), the value of sHlthExpPcntGDP is not allowed to decline over time.
3.5.5 A note on equilibration of government revenues and expenditures
The specifications described for government revenues (GOVREV) and expenditures (GOVEXP) allow the computation of the annual balance (GOVBAL). Governments are very seldom able to exactly balance revenues and expenditures, but over time there are constraints on the extend of deficits they can run and the financing of those. IFs uses a dynamic system with attention to changes in stocks of debt or assets associated with GOVBAL over time. The documentation of intertemporal dynamics and equilibration in Section 4 elaborates that system.
3.5.6 Extensions of forecasting to central and local government finance
The government finance system initializes four local government finance variables for a country as a whole, namely
GOVREVLOCAL (local government revenues)
GOVEXPLOCAL (local government expenditures)
GOVCONLOCAL (local government direct consumption)
GDSLOCAL for categories health and education (local government consumption by type)
These variables are given values in the preprocessor. In the Base Case scenario, however, they are constant across time. They are available for use in specialized projects, most of which have involved elaborating specific countries into subunits such as states, provinces, or districts.
In addition three variables have been added as placeholders that would add complexity and possible utility to representation of government finance at the sub-national level:
GOVREVCENFRLOCAL (government revenue at the central level from the local—transfers)
GOVREVLOCALFRCEN (government revenue at the local level from the central—transfers)
GOVREVLOCALTAX (government revenue raised through local taxes)
In current default use of the model the values of this second set of local government variables are zero across time.
It would take very considerably more work to make truly dynamic the central and local government finance variables of all countries in Base Case and other analysis that did not involve elaborated analysis of subunits within countries. There are two very different circumstances for such representations:
1. In integrated local representation without regionalization of countries. Steps of complexity: (a) local shares could be raised or lowered with functional forms or exogenous multipliers, with no forward linkages in model version with no specific representation of sub-units, having no real model impact; (b) passing through local changes to total revenues or expenditures as straight increases or decreases; for instance, if total expenditures were pushed up by an exogenous increase in local expenditures, it could have broad impacts on revenues as well as on the targets of those expenditures. But it is not clear that (b) would add much model value because exogenous changes to total revenues and expenditures are already possible.
2. In regionalized (states, provinces, districts) local representation. The IFs project has worked with national or local governments in countries including South Africa, Uganda, and Brazil to forecast at the sub-national level; data for sub-national levels have been added to the model for other countries including China, India, Mexico, and Nigeria. Using South Africa as an example, such work is heavily complicated by the fact that the model cannot now simultaneously represent both central government (e.g. national level government in Pretoria) and local government finance (e.g. in Western Cape), much less the interaction of the two and the possible implications for other provinces. The total government numbers being brought into the model for all SA provinces represent values related to provincial-level initialization―the model effectively treats them as countries, allowing aggregation from regions up to the total but not distinguishing between regional and national finance.
A first step might be (a) to provide initialization data for as many as possible of the 7 variables for sub-national regions and make sure the preprocessor uses these when available instead of estimates; (b) to initialize total government for sub-regions as mirrors of national government, making all provincial total variables essentially identical shares of the national total percentage rates. The two elements of this step would be complicated, but reasonably limited.
A second and considerably larger step might be (c) to allow manipulation of provincial local expenditures with pass through to total (actually, the provincial shares of the total) as indicated in point 1 above.
A much bigger step would be (d) to think about trade-offs and interactions across expenditures and revenues within and across local and total levels. It would then be possible, for example, to push up a specific consumption expenditure (say that on education) and boost educational performance and downstream impacts of that within one region, representing the trade-offs with (i) other expenditures in that region (this can already be done, but not always with meaningful provincial financial numbers) (ii) offsetting revenue increases at the local level (assuming there is any local sourcing of revenue); (iii) transfers from the regional total representation to or from the local; (iv) some combination since there would be many possible ones. In general, representing trade-offs outside of the specific region would be especially messy.
In spite of the limitations of IFs with respect to separately representing and then connecting central and local finance, the system has proven useful in selected sub-national region analyses.
3.6 International Actors and Financial Flows
Conceptual foundations for accounting of international flows and stocks build largely around two flow concepts in the economic literature: current account balance (CURACT) and capital account balance.[3] In recent years, most items in what have long been understood as the capital account have been identified by the IMF as the financial account (IMF 2009: 216), with a smaller set of items identified as the capital account. We will here continue to use the more traditional economic literature conceptualization. Both current and capital accounts represent annual flow variables, their totals being essentially equal with opposite signs.
Current account definitionally equals the sum of (1) trade balance (TRADEBAL), inside IFs being relative-price adjusted exports (XRPA) minus imports (MRPA), (2) unilateral transfers, with IFs representing the net outflow of foreign aid (AID) and foreign workers’ net remittances to home countries (XWORKREMIT) but not pension payments to retirees living abroad, and (3) income transfers/investment income such as the rents, interest, profits, and dividends paid on past capital flows for which IFs calculates an internal variable (Interest) that would benefit from extension and refinement).
Capital account equals net capital flows (the change in short-term and long-term asset/debt stocks). These flows include foreign direct investment (XFDIFIN and SFDIFOUTD), portfolio investment (XPORTFIN and XPORTFOUT), and loans from international financial institutions (XWBLNFIN, XWBLNFOUT, XIMFCRFIN, and XIMFCRFOUT). In addition, the capital account (or financial account in the newer IMF nomenclature) represents net change in the stock of international government assets/debt (XGOVTBDEBTF).
Most of the sub-subsections that follow this introduction lay out the elements of the current and capital accounts within IFs. They will discuss total trade magnitude and balance of countries, foreign aid and worker remittances (two additional elements of the current account), and then move to FDI and portfolio flows, two critical elements of the capital account. Discussion will then turn to flows from and to international financial institutions, which are also placed in the capital account.
Yet, whereas the current and capital accounts are annual flows, Faruqee (1995: 84) emphasizes, as is the case in IFs, that the determination of exchanges rates requires a stock-flow perspective: “…a sustainable capital account position is based on the underlying determinants of net foreign asset equilibrium.” The final two sub-subsections will thus move from flows to stocks.
The next major section of this documentation (Section 4) treats equilibration dynamics across the economic model and will elaborate how the stock of international debt affects exchange rates. And Section 5 explains the elaboration of many of the financial flows discussed in this one (especially trade, foreign aid, and FDI) from monadic (country total inflows and outflows) to bilateral (inter-country or dyadic) flows. That bilateral elaboration does not affect the country totals of interstate flows and therefore does not affect the national social accounting system flow representation described here or the equilibrating dynamics around them described in Section 4.
3.6.1 Monadic (country total) trade
The IFs structure treats trade (and some other international flows) in two steps. The first computes each country’s total level of exports and imports using a pooled approach. That is, it does not in this step represent country-to-country (bilateral or dyadic) trade flows, but it represents instead national trade into or out of a global pool of total trade flows. A second step, documented in Section 5, addresses the bilateral or dyadic (country-to-country) flows of trade, activated in IFs optionally via parametric choice (bilateralsw, default=0) when running the model, which elaborate international trade patterns but do not directly affect the SAM structure. Other trade models with generally much shorter horizons often build trade flow representation at the dyadic level and then sum across country partners to represent total national exports and imports. One reason for the top-down-approach alternative in IFs is that it facilitates incorporation of longer-term drivers of national export and import trade totals, such as temporally cumulative trade imbalances and other financial drivers of exchange rates.
Almost all modeling of trade drives changes over time by a combination of production, income, and price variables, linked to changes in trade via income and price elasticities. IFs does the same, but uses an equilibrating structure that is fundamentally the same as that that used for other variables in the SAM that require attention to balancing demand and supply processes with flows and stocks. Section 4 elaborates that structure with its attention to attention to variables signaling disequilibrium (namely domestic prices (PRI) and exchange rates (EXRATE)) that shape changes in flows (namely sectoral imports (MS) and exports (XS)). In addition, because IFs forecasts over such a long horizon, it is important to specify changing propensities for export capacity (XC) and import demand (MD) based not just on current bases for exports and imports (XBASE and MBASE), rooted in domestic production and demand, but tied to stock-like variables that signal likely shares of those production and demand variables to be traded (XKAV and MKAV).
The above equations elaborated in Section 4.4.4 to compute sectoral exports and impots are necessary only for four of the six economic sectors. The agriculture and energy models compute trade in those sectors separately, again in equilibration processes. Given the computation of sectoral exports and imports (XS and MS) for all sectors (across the general and partial equilibrium models), it is possible to compute total exports (X) and imports (M).
IFs also computes these in a "relative-price-adjusted" form, multiplying the real sectoral values by global prices (WP). Why is this important? If, for example, a country is highly dependent on energy exports and the global price of energy (from the energy model) doubled relative to other prices, failure to adjust trade for prices would understate the country’s trade balance. It is the relative price-adjusted trade that is taken to the international financial calculations of the SAM.
A purely optional adjustment to the relative-price-adjusted import and export levels is available for the model user who wishes in scenarios to examine the hypothetical impact of changes in the terms of trade. The terms of trade parameter (termtrm) is a multiplier with a default value of 1.0. Higher values shift the terms of trade in the favor of Southern or less-developed regions (those with initial GDP per capita less than an amount, such as $5,000, specified by nsdiv) and lower values favor Northern regions. The determination of North and South is by initial GDP per capita and the fixing of those categories is important.
If then
If then
The adjustment to regional exports and imports for hypothetical terms-of-trade change can result in a failure of exports and imports to sum across regions to the same global total. At this point IFs thus renormalizes regional exports and imports to a total value for world trade equal to the average of the price-adjusted sums of exports and imports across regions.
Given final values for regional, price-adjusted and terms-of-trade-influenced exports and imports it is possible to compute regional trade balances (TRADEBAL), using the relative-price-adjusted exports and imports.
3.6.2 Foreign aid
Although early code is in place to represent of foreign aid bilaterally (see Section 5.5), as with trade IFs currently uses as a default a "pool" approach to aid (AID) rather than indicating bilateral flows from specific donors to particular recipients. That is, all aid from all donors flows into the pool and then all recipients draw proportions of the pool.
IFs uses the aid value parameter (aiddon) to calculate the aid (AID) from donors as a percentage of GDP; that parameter is constant in the Base Case and can be modified by scenario. Total aid available from donor countries is summed annually in a global pool of aid.
In the first model year IFs calculates aid received (initialized in the data preprocessor) as the percentage of GDP that it constitutes for recipients (AIDREC, a variable that does not actually vary over time).
Over time, the share of GDP constituted by aid received tends to decline, in part because the GDP of recipients tend to grow faster than that of recipients, but also because less aid may be needed. In IFs, as the GDP per capita at purchasing power parity (GDPPCP) of recipients grows toward an aid graduation level target (aidgradpoint) the aid to be received as a portion of GDP (AidRecPcnt) calculated in an algorithmic logic (AL) declines. An exogenous multiplier (aidrecm) can modify that percent received.
Percentages of GDP constituted by aid receipts (desired) and donations (specified) allow an initial calculation of net foreign aid for each country.
At this point in calculations, global sums of net inflows and outflows will not match, so the need to be balanced. Net aid outflows (donations) are negative and the total aid pool given (AIDP) is the sum of the negative flows, while the total desired aid of recipients (AIDR) is the sum of positive desired inflow
if
if
The pool of aid donations determines the actual total level of interstate aid flows and is allocated among potential recipients according to the proportions targeted for each,
if
3.6.3 Worker Remittances
Worker remittances are tied closely to the migration formulation of the IFs demographic model (see the documentation of that model). In recent years the representations of migration, foreign-born populations within countries, and remittances have been changed from net inward and outward values to gross values. Hence, IFs includes variables for MIGRANTSIN, MIGRANTSOUT, POPFOREIGNIN, POPFOREIGNOUT, XWORKREMITIN, and XWORKREMITOUT. Further, the representation of migration among countries has been elaborated to include an optional analysis of bilateral migration (see Section 5 of this documentation. Representation of remittances has, however, remained monadic, albeit now being gross inward and outward values.
The IFs migration module once relied heavily on UN data for past migration levels, also tapping their near-term forecasts. The IFs preprocessor and model now rely primarily on migration data from the International Institute of Applied Systems Analysis (IIASA). The preprocessor has quite extensive algorithms to reconcile that migration data with remittance data, and migration and remittance data from the World Development Indicators with foreign population data (from the same source).
Initial data on worker remittances, added to the IFs database as a percentage of GDP, come from the World Bank’s WDI, as do data on foreign population as a percentage of the total. The original sources were Global Development Finance and the OECD, respectively. At one time the worker remittance series only included data by country of receipt, forcing us to estimate remittances by countries of origin in the preprocessor on the basis of the foreign worker series. Now remittance flows in and out are reported, but there are still balancing issues.
The data do not, however, exist for global representation of dyadic remittance flows, that is, of flows from country of origin to country of destination. IFs therefore uses a pooled approach, representing aggregate remittance flows out of countries and aggregate flows into countries, requiring that they be balanced, but not attempting to trace dyadic patterns.
The specific formulation for outward flow of remittances (XWORKREMITOUT) multiplies the foreign-born population calculation (POPFOREIGNIN) by a ratio computed the first year (RemitPerWorkerOut) of outward remittance flows per foreign born and the GDP per capita of that year. This ratio thus scales the remittance amount to GDP per capita (at MER) and uses that scaling to effectively increase the outward flow per foreign born individual over time.
where
The exact same logic is applied in reverse to calculate the remittances flowing into a country from population sent abroad.
where
There are many obvious limitations to this approach, including the uncertainties at any point in time and growing over time of the demographic characteristics of migrants and foreign-born populations. Further, the inward remittances more logically should be tied to the income levels of a country’s population abroad rather than to the receiving country, something that would require a bilateral representation and knowledge of where the population abroad might have gone. Yet, the general logic helps tie remittance flows over time to both population flows and income levels of flows outward and inward.
The last step in this process is normalization of remittance outflows and inflows to a global sum value that is put at the average of the sums from the above equations.
3.6.4 Foreign Direct Investment
For most of the substantive areas within IFs for which component models represent both stocks and flows, the structure of representation involves a focus on formulations for flows, a calculation of changes in stocks resulting from those flows, and very often a set of feedbacks from levels of stocks to flow rates in future years. A foundation for such logic is the recognition that stock levels of variables such as indebtedness face limits.
The logic within IFs around foreign direct investment (FDI) is focused much more directly on the levels of stocks relative to GDP, from which flows are computed. The typical pattern of FDI investment is that firms direct FDI from relatively capital-rich countries to relatively capital-poor ones. Estimation within the IFs project reinforced that presumption in analysis of patterns found in the IFs database (using FDI data from the World Bank’s World Development Indicators and from UNCTAD). A less steeply sloped line is the relationship between GDP per capita at PPP and the stocks of FDI inflows as a ratio to GDP. A more steeply sloped line is the relationship between GDP per capita at PPP and the stocks of FDI outflows as a ratio to GDP. Both lines are upward sloping and, in fact, countries are simultaneously larger sources and targets of investment, even relative to GDP, as they develop. Roughly speaking, countries are net recipients until GDP per capita is somewhat above $20,000 and net sources thereafter.
IFs recognizes that these patterns will not be universal. Thus, the algorithm that determines country-specific outward stocks of investment is one that builds on the historical pattern of FDI net inward and outward stocks and flows, but that assumes some convergence in generalized patterns of stock ratios to GDP only over a very long period of time, such as a century. The same is true for recipients and stocks of inflows. It might be reasonable to posit that both lines would shift to the right over time as the average per capita levels of global GDP increase. We have not built that presumption into the model at this time.
In addition to the relative behavior of firms in states across the system, another behavioral issue is the overall pattern of increase or decrease in FDI flows relative to the size of the global economy. Over the last several decades FDI has grown steadily as a portion of the global capital stock and global economy. Economic historians are, however, quick to point out that the turn of the 20th century was a period of enhanced globalization of capital and that those flows then retreated for most of the 20th century before advancing again. And this century has already seen some at least temporary retreats. The base case presumption built into IFs is of growth in FDI flows in near-term years at a rate that exceeds economic growth but that convergences towards GDP growth across 100 years.
The representation of FDI in IFs builds from the concepts and general theory around FDI stocks that estimation and the above discussion suggest. In each time cycle the model computes stocks of both inflows and outflows. As a first step, the expected stocks of inflows (ExFDIStockIn) are a fraction of GDP (FDIRatio), with the ratio gradually converging from the initial condition for each country (XFDIGDPIn) to the pattern of global ratios expected as an analytical function of GDP (ExpFDIRatioIn).
where
where
Exactly the same logic applies to expected stocks of outflows (ExFDIStOut).
where
where
Without further modification, the above formulations would result in stocks that fully determined the annual inflows and outflows. There are, however, empirical initial conditions for such annual flows that should not be ignored, especially in the early years of forecasts; the late 1990s were, for instance, a period of high flow rates that would not be captured by the above formulations.
Thus, the formulation has a second step built around flows. Based on the above-expected stocks of FDI inflows (ExFDIStockIn), actual stocks (XFDISTOCK) are computed using a rate of growth (FDIRIn). The user can further intervene in the stock specification with a multiplier (xfdistockm). The rate of FDI stock growth converges from an initial rate (XFDIStockR) tied to empirical inflows to an exogenous rate (xfdistockr).
where
where
Again the logic is the same for outward flows and stocks.
where
where
There can be in the formulations above some tension between the convergence of stock patterns to the analytic function for stocks as a portion of GDP and the convergence of them towards annual growth as specified in the exogenous parameter for rate of stock growth (xfdistockr) with its default value of 3.0% annually. Yet, the multiplier parameter (xfdistockm) gives the model user great control over the growth of country-specific inward and outward stocks of FDI.
There is one additional element of the formulation for FDI that is in place for model use in global scenarios. Multiplicative (xfdiwgrm) and additive (xfdiwgrmadd) parameters are in place to modify the global growth patterns of FDI inward and outward stocks It is sometimes desirable for a user to be able to simply specify a rate of global growth in FDI (including potentially sharp retrenchments in FDI) and impose the resulting global FDI levels (WFDI) on the above formulations, letting the above equations determine country/regional stocks and flows within the global constraint.
This formulation element uses a rate of growth (WFDIR) in the ratio of FDI to world GDP (WFDIRGDP) that is set to move from the initially calculated growth rate (WFDIFRI) of world foreign direct investment relative to GDP growth to 0.5% (now hard-coded in a specification of WFDIGr) over the first 20 years of the model run. The calculation accounts for the expected depreciation rate of the FDI stock as represented by the lifetime of manufacturing capital (lks).
As a default, however, xfdiwgrm is set to 1. In that case, an alternative calculation of WFDI can be influenced by an additive term controlled by xfdiwgrmadd with a default value of 0.5 (in model version 7.94), thereby building in some longer-term growth to global FDI relative to GDP growth.
or, if xfdiwgrm = 1 then
where
One additional change can be made to WFDI. It was introduced to IFs in analysis of scenarios involving major and unexpected extensions of life expectancy (WlifExpTerm), which might be expected to increase global FDI in response to changing life-time savings and investment patterns. The parameter that controls its impact is elfdilifexp (with a default value of 0.05); normally this adjustment will be negligible.
where
Once WFDI is determined, it is used to normalize the country/regional calculations of stocks (XFDISTOCK and XFDISTOUT)—that routine normalization is not shown in the equations. The annual changes in the ultimate values of stocks then provide gross annual inflows and outflows.
Obtaining data for initialization of the stocks and flows of FDI posed some challenges. UNCTAD’s annual World Investment Report had some data on stocks, but they proved difficult to obtain electronically. We therefore turned once again to the World Development Indicators, even though that source provides only flows. It does, however, basically provide both net inflows and net outflows (XFDIFIN and XFDIFOUT). Because of the instability in these numbers over time, the last five years of data were averaged to compute initial conditions for annual flows in the model.
Integrating the flows from 1970, on the assumption that there was considerably less FDI prior to post-1970 surge of globalization, provided estimates of stocks that seemed reasonable when checked against some of the UNCTAD stock data. But because these do not necessarily yield the same totals for global inflows and outflows, the two sets of numbers were summed for their respective totals, and inflows and outflows were normalized to their global average. The result was initialization of FDI stocks from abroad (XFDISTOCK) and FDI stocks held abroad (XFDISTOUT).
3.6.5 Portfolio Flows
The algorithms behind portfolio flows, again involving firms in large part but also introducing behavior of households, are essentially the same as those for FDI. And again, model users can intervene to change either individual country/region patterns or systemic growth of portfolio flows.
With respect to portfolio investment, WDI provides flow data on both bond and equity investment. Averages of the most recent five years were used to compute initial conditions for annual flows, and annual flow data were integrated from 1970 to obtain estimates of portfolio stocks held in developing countries (XPORTFOLIO). Unfortunately, the WDI provided only flows into developing countries and the data fail to account for the source of the flows. Therefore, the asset balances were assigned by GDP weight in the preprocessor to developed countries (XPORTSTOUT).
In each time cycle the model computes stocks of both inflows and outflows. As a first step, the expected stocks of inflows (ExPortfolio) are a fraction of GDP (PortfolioRatioIn), where the ratio gradually converges from the initial condition for each country (XPortGDPIn) to the pattern of global ratios expected as an analytical function of GDP (ExpPortfolioRatioInComp).
where
where
Without further modification, the above formulations would result in stocks that fully determined the annual inflows. There are, however, empirical initial conditions for such annual flows that should not be ignored, especially in the early years of forecasts; the late 1990s were, for instance, a period of high flow rates that would not be captured by the above formulations.
Thus, the formulation has a second step built around flows. Based on the above-expected stocks of portfolio inflows (ExPortfolio), forecasted stocks (XPORTFOLIO) are computed using a rate of growth (PortfolioRIn). The user can further intervene in the stock specification with a multiplier (xportfoliom). The rate of portfolio stock growth converges from an initial rate tied to empirical inflows to an exogenous rate (xportr).
where
The same logic applies to portfolio outflows, starting with a computation of expected outward stocks.
where
where
The expected outward stocks can then be modified to make them more compatible with initial data and user interventions.
where
where
The world sums of stocks for portfolio inflows and outflows will not be identical. IFs computes a world total of flows (WPortfolio) as a step towards imposing it on both. The user has scenario control of growth via a multiplier parameter (xportwgrm). Note: the actual sequence of computation puts this global sum computation before that of country-specific values.
where
The inward and outward stocks are then normalized to a global total (WPortfolio), which is the average of the global sums of each that were computed above.
After the logic of the stock-driven formulation is played out, the final determination of flows is identical to that for FDI except that there is no physical depreciation around portfolio investment.
Ideally foreign direct investment and portfolio investment would be responsive to equilibrating mechanisms. In reality, that is not always the case. FDI and portfolio flows can be, in fact, somewhat perverse, moving from fear or greed in opposite directions to the needed balances. At this point, no linkages of any kind have been added to these flows from exchange rates, liquidity levels, or other elements of the equilibrating mechanisms to be discussed in Section 4.
Also, there is through version 7.94 no representation of dynamics for direct firm borrowing and lending across country borders. Instead there is a simple growth equation for net external debt. External firm debt is added to external government debt in the calculation of total external debt of countries, thereby affecting exchange rates (see Sections 4.3.4 and 4.5.5); its simple representation here means that the real driver of those exchange rates is external or foreign government debt, the broadest definition of which in IFs also includes current account imbalances. Thus, the absence of such imbalances in this simple equation for external firm debt does not mean that current account imbalances fail to pass to exchange rates.
3.6.6 International financial institution flows
The international financial institutions (IFIs) are agents of importance for countries around the world. This section explains a basic agent representation of the World Bank and a less-fully elaboration representation of the IMF.
With respect to World Bank agency, the formulations of IFs fall generally into four basic decision categories: How much to loan? To whom to loan? For what purposes to loan? At what terms to loan?
Concerning the total that the bank has to loan at any given time (XWBLOANSTOT), that is a simple sum of lending capacity last year plus repayments (XWBLnRepayTot), minus new loans (XWBLnNewTot), and plus new subscriptions (XWBLnNewSubTot), the last term modified by the loan to equity ratio maintained by the Bank (xwblneqr). Repayments or the flows out of countries to the Bank (XWBLNFOUT) depend on total lending to the countries (XWBLOANS), the real interest rates charged by the Bank (wblintr) and the repayment rates in years (xwblnrepr).
The World Bank and its member countries collectively determine the rates of growth in new subscriptions (XWBSUBF), but we represent that with an exogenous parameter (xwbloanr). IFs does not attempt to maintain cohorts of loans to different countries. Nor does IFs track the administrative overhead of the Bank, which could significantly reduce lending capacity over time.
where
With respect to the countries to which it lends, IFs focuses primarily on determining flows as a percentage of GDP. This is different than the approach to representing FDI or portfolio investment in part because those representations were driven almost entirely by changes in GDPPCP. In the case of World Bank lending, estimates that it targets flows based on two additional characteristics of the borrowing country: the Gini coefficient of inequality (GINIDOM), and aid as a percentage of GDP (AIDPERGDP) that countries receive as official development assistance (ODA) from countries. A more extensive analysis is documented elsewhere (Hughes and Hossain 2003). For instance, GDP per capita and the Human Development Index (HDI) are close substitutes in correlations with Bank lending. After extensive exploration, it was decided to build in IFs a three-variable representation of Bank decision-making concerning the countries to whom it lends. All else being equal, that analytical function produces a statistically predicted value of loans to each country.
The function above provides the foundation for a three-step representation of the country-specific lending flows from the bank (XWBLNFIN). The first step is to compute a base value for flows to each country (XWBLnFINBase) simply by scaling up each country’s initial year lending receipts (XWBLNFIN) by the growth in total World Bank lending relative to the first forecast year. Computing such a base is valuable because it introduces the drivers of lending that are not captured in the predictive formulation (the three variables capture about three-fourths of the variation).
The second step is to compute an adjusted forecast of lending (XWBLnFINAdj), taking into account the changes suggested by the predictive function from initial year values. The adjusting factors come into the equation as a ratio of the purely predicted lending rate in the current year over that rate in the initial period.
The third and final step is to normalize the adjusted forecasts to the total of new World Bank lending. This step also allows the user to force changes in lending to specific countries via an exogenous multiplier (xwblnfinm).
The outstanding loan portfolio for each country can then be updated.
The third decision of the World Bank as lending agent was specified to be the target sector of loans within recipient countries. In large part because of the other models and variables within IFs, five such targets are specified: education, health, unskilled worker households, skilled worker households, and other uses. At this point in model development a single parameter (xwbsectar) has been added with default values that draw upon data gathered about past Bank practice to guide flows to uses within recipient countries. A final adjustment term (XWBFlowsAdj) is put unto that equation based upon algorithmic analysis in the first year; for instance, if it is found that supposed World Bank lending to the education sector exceeds government spending in that sector, the adjustment factor reduces it.
The fourth and final set of decisions concern the terms of the lending. Again, parameters exist to change interest rates (xwblintr) and repayment periods (xwblnrepr). Currently, returns of funds to the World Bank and the IMF are assumed in the base case to be at the rate of 5% of principal each year, with 3% real interest payments, about the rate of global economic growth.
The IMF representation is fundamentally parallel to that for the World Bank. It determines in the same manner how much credit the IMF has to offer. And it determines the initial target of credits based on the scaling up of initial credits, the process that computed a base calculation for the World Bank. There is no representation of IMF agency based on analysis around the drivers of its credit offering over time (such as liquidity problems of recipients); instead credit levels are now changed over time with potential GDP (GDPPOT) of recipients and an exogenous multiplier (ximfcrfinm). Agency could be developed analogously to the representation in the World Bank, although the real-world IMF process is more politically charged than are Bank lending decisions.
Over time the total stock of credits that the IMF has available to provide (XIMFCREDITTOT) is the accumulated sum of three terms. The first of those is the global sum of new annual subscription flows to the IMF by countries (XIMFCrNewSubTot), for the most part high-income ones, modified by the IMF’s operating ratio of credits provided to underlying subscription equity (ximfcreqr) – that parameter has a default value of 5. The second term is the global sum of repayments to the IMF from countries receiving them earlier (XIMFCRRepayTot). The annual flow term that reduces credit offering potential stock of the IMF is the annual flow of new credits to all countries (XIMFCRNewTot)
The global sum of annual flows of new subscriptions by donor countries to the IMF (XIMFSUBF) and is determined by a parameter specifying the growth in IMF credits (ximfcreditr) from the prior year, a parameters with an default value of 3 (hence 3 percent).
where
Turning to repayments, the flows out of recipient countries (XIMFCRFOUT), depend on the payment of both interest rate (ximfcrintr) with a default real annual rate of 3 percent and principal (at ximfcrrepr) with a default value associated with a 15-year repayment period.
where
The third term carries the sum of new credits provided to recipients (XIMFCRFIN), beginning with a preliminary calculation of those credits, computing that preliminary calculation by simply scaling up the flows given to each recipient in the base year of the model by the growth in total credit offering potential of the IMF over years from the first.
where
Although this preliminary calculation is used as the third term in the computation above of total IMF credits (XIMFCREDITTOT), it does not represent changes in the division of those credits across countries. That division is accomplished in two steps. The first is the scaling up of first year flows to countries by growth in the potential GDP and by an exogenous multiplier (ximcrfinm).
The second step in computing IMF credit flows to countries is normalization across countries so that the total global flows computed above on a preliminary basis still hold.
where
Given the final calculation of IMF credit inflows, it is possible to compute the total IMF credit position (XIMFCREDIT) of each country around the world (which will be negative for subscribers and positive for countries new net credit inflows).
There were many data-related issues and decisions made to initialize the World Bank and IMF representations. The WDI database provides information on annual loans from the World Bank in two categories, those of the International Bank for Reconstruction and Development (IBRD) and those from the International Development Bank (IDA). The latter loans tend to have more concessional terms than do the former. Similarly, the database provides information on annual credits from the IMF, dividing them into concessional and non-concessional.
For the purposes of the SAM at this stage, the preprocessor sums the two types of loans and two types of credits into a total annual lending by the Bank and total credit flow from the IMF. Because these values tend to fluctuate substantially from year to year, and because the final years of the 1990s were a rather unusual period in global financial markets, the values set for initialization of forecasts are calculated from 5-year averages of loans and credits received as a percent of GDP in recent years, with the average rate then applied to the GDP of developing countries in the model's base year.
Unfortunately, the data only indicate net flows. For purposes of the dynamics of the model, it is important to distinguish repayment of loans or credits and interest on loans from new inflows. Net flows from the World Bank were decomposed into estimates of inflows (XWBLNFIN) and outflows (XWBLNFOUT) by estimating the value of repayments (outflows) based on the stock of loans from the Bank. The estimate of outflows assumed a 20-year life on loans and therefore 5% annual repayment, as well as a 3% interest rate via parameters that have are available for intervention by users. New inflows were then calculated as net flows minus the outflows. The same process was followed for IMF credits.
3.6.7 Current Account
The current account of countries interacting with the rest of the world includes trade in goods and services; income on assets (such as rents, interest, profits and dividends); and various transfer payments (including foreign aid, government subscriptions to international organizations, pension payments to workers living abroad, and foreign worker remittances to their home countries).
IFs computes the current account balance from the conceptual elements indicated above. Although actual foreign direct investment and portfolio flows belong in the capital account (see below), the net interest earnings on the assets abroad and in-country belong in the current account. In the formulation below for Interest, not all government or firm debt is represented as a basis for generating international flows, only international government debt (XGOVTDEBT, not GOVDEBT, which is also different in that in IFs it is a percent of GDP) and only international firm debt (XFIRMDEBT).
where
Some of the above formulation is focused on determining the implicit (not explicitly and separately represented in IFs) net interest, profit, and dividend flows, which are specified as an exogenous real interest rate (lintr) times the net stocks of assets discussed earlier. During work on the PID in 2021, however, the Interest term was removed from the calculation of current account because the formulation for it appeared inadequately strong; that issue should be revisited.
3.6.8 Capital account
As indicated earlier, capital account equals net capital flows (the change in short-term and long-term asset/debt stocks). The underlying flow and stock variables include foreign direct investment, portfolio investment, and loans from international financial institutions. In addition, the capital account (or financial account in the newer IMF nomenclature) represents net change in national government reserves.
The government reserve stocks have a prominent role in representation of international balances and they play a fundamental role in the model’s computation of changes in exchange rates. In a step toward representing government financial stocks, IFs separately sums the elements of capital account other than net change in reserve stocks, calling the variable capital account limited (CapActLim).
IFs computes the limited (or partial) capital account balance from the elements of the capital account over which the government normally has least direct control. The limited capital account balance purposefully excludes the short-term equilibrating elements of changes in reserves and short-term government compensatory borrowing.
where
Almost always the sign of CapActLim will be opposite that of CURACT; e.g., a negative trade balance requires an offsetting positive capital inflow. The sum of them will not, however, be exactly 0 and governments will typically make up the difference with a change in reserve holdings or short-term borrowing.
3.6.9 Net annual change in foreign assets and liabilities
IFs represents the annual net changes in government reserves as a residual term, the difference between the current account and the limited capital account. Because the government’s central monetary authorities are responsible for managing this residual, its name in IFs represents the annual change or flow in the basic external government debt (XGOVTDEBTBF).
Specifically, the annual foreign balance (the flow captured in XGOVTDEBTBF) is the negative sum of the current and capital accounts, negative because if, for instance, imports exceed exports making the trade and current account balances negative, that adds to debt accumulation (or reserve reduction). This variable is important because it is effectively the change that will occur automatically in foreign reserve levels.
As we shall see in Section 4, the equilibration process takes place around the stocks of those reserves and other indebtedness to which governments must pay special attention.
3.6.10 Net foreign asset and liability stock (net external debt)
Foreign assets can consist of gold, banks loans, debt held, direct investment, and equity, plus reserve assets.[4] Governments, firms, and households can have foreign assets and/or liabilities. IFs has no structural foundation for determining foreign asset/liability positions of households; those of governments and firms are generally more significant in any case and are the focus here.
Although foreign aid is treated only as an annual flow in the computation of current account, a significant portion of foreign aid consists of loans. Therefore, in calculating the stock of basic external government debt (XGOVTDEBTB) as the sum of the flows (XGOVTDEBTBF) over time, that loan portion (LoanPortionAid) is also added to the annual calculation. Similarly, annual net credits from the IMF and loans from the World Bank, while augmenting (or decrementing) the capital account, also contribute to long-term responsibilities of national governments. They are therefore further added to the basic external debt position in the calculation of a fundamentally total representation of external government debt (XGOVTDEBT).
The annual flow imbalance of the two international accounts can be accumulated in a stock variable (XGOVTDEBTB) representing the increasing (or decreasing) requirements for government to address via changes in reserves and changes in debt in the face of discrepancy between the current and limited (reserve-excluding) capital accounts. The naming of it as a debt term emphasizes the pressure that positive values put on exchange rates if they grow (lower or negative values would be consistent with increases in reserves or decreases in shorter-term borrowing of foreign currency). The initialization of it as total external public, publicly guaranteed, and private nonguaranteed debt (variable name and data series XDEBT) emphasizes also the ties of the exchange rate system broadly to foreign debt.
In addition, the loan portion of foreign aid (LoanPortionAid), determined by the parameter aidlp, is added to the variable because all of AID was put into CURACT as a unilateral transfer, but in reality the loan portion is an addition to governmental foreign debt to which the government and exchange rates are sensitive).
where
Total external governmental debt stock (XGOVTDEBT) is set as the basic debt plus stocks of IFI credits and loans, notably the accumulated outstanding balances of IMF credits (XIMFCREDIT) and World Bank loans (XWLOANS). The loans are generally development oriented (and barring forgiveness need to be repaid by governments). IMF credit inflows are actually often provided as shorter-term loans for addressing pressures on the foreign exchange, but the accumulated balance of them, again barring forgiveness, is a debt affecting governmental balance sheets.
While governments are responsible directly for the elements of XGOVTDEBT and must assure that they do not become overly large relative to the size of the GDP (and the government’s share of that), many fluctuations in exchange rates, including those during financial crises of countries like those in Asia in the late 1990s, are responsive also to overly large burdens of external debt incurred by firms (XFIRMDEBT). IFs does not have a representation of dynamics underlying firm borrowing abroad and such debt. It therefore represents its growth over time simply as occurring at the same rate of average long-term global economic growth, specified in hard-coding as 3 percent annually. That firm debt is added to the external government debt (XGOVTDEBT) in the computation of a broader external debt variable (XDEBTRPA). That broader debt variable is relative price adjusted, as is the trade balance in the current account foundation of it. The variable is the representation in IFs of the external debt that national financial authorities including central banks must keep within controllable magnitudes.
As discussed in the introduction to this section, total external debt (stock of foreign account imbalance) is in IFs the sum of basic governmental indebtedness and firm debt. In reality, the simple treatment of firm debt has no significant impact on the debt that influence exchange rate dynamics of the model.
Particularly in shorter-term analysis of international finance of countries, the concepts of international reserves and foreign currency liquidity are important.[5] Although IFs does not explicitly project reserve stocks as a result of changes over time in representation of international financial variables, it has developed an initial representation of a target variable for reserves as a percentage of GDP (XRESERVES) and at some point the addition of an actual reserve variable could occur. Currently the equations for XRESERVES (not shown) simply converge the base year data value for those reserves as a ratio to GDP toward 15 percent. It would be possible to introduce a computed value of reserves by changing the data value for them in the base year with the annual change in XDEBTRPA, allowing then a comparison of that computed value with the target variable. That would make useful a liquidity variable included in IFs and computed now as a ratio of current account to the target value of reserves; it is now effectively a target value for liquidity and could be converted to a computed value.
Section 4 documents how XDEBTRPA drives changes in exchange rates and thereby helps maintain reasonable levels of current account imbalance and government ability to manage those imbalances with reserves.
3.7 Savings and Investment
This documentation of the flows in the social accounting matrix has explained the computations of government, household, and firm savings. The only element missing for the calculation of total savings is foreign savings (savings from abroad). Foreign savings is basically the flipside of the current account balance—a deficit in the current account must be offset by an inflow of foreign savings. Hence everything that improves the current account, such as more exports, reduces the net inflow of foreign savings. In IFs foreign savings (FORSAV) have terms from net trade, aid, remittance flows, and tariff revenues on imports.
The total savings in each country (SAVINGS) will be the sum of the individual terms.
In other sections of this documentation we have described the computation of relative-price adjusted variables such as exports (XRPA), imports (MRPA), and GDP, potential and actual (GDPRPA and GDPPOTRPA). In addition we have relative price adjusted versions of foreign savings (FORSAVRPA) and total savings (SAVINGSRPA).
These relative-price adjusted savings variables are used for information only and do not affect financial balances or other variables. The relative-price adjusted trade, however, is taken to the trade balance (TRADEBAL) as shown in Section 3.6.1, and it therefore affects the current account balance (CURACT) and international debt calculations (XDEBTRPA).
Definitionally, SAVINGS should equal investment (I), defined as capital formation (IGCF) plus inventory stock (ST) changes. Looking at the two variables side by side is a good test of the functioning of the SAM at any time point and of the equilibration processes that control its flows over the long term. The complexities of the accounting in the SAM complicate maintaining that identity with ongoing model development, but it something that IFs developers work hard to maintain.
Even when the identity is maintained, however, the magnitude of inventory stocks as a portion of I can vary substantially over time both in absolute terms and relative to target levels. For instance, if demographic structures and aging population encourage households to save more and consume less of their disposable incomes, even though the Savings and I identity should be maintained the rise in savings may at least initially coincide with inventory stocks (ST) overshooting their targets rather than IGCF rising. Similarly, a rise in government spending on education not paid for with revenue increase can lower the government balance (GOVBAL) and thus savings overall, but that same spending might at least in the short run lower inventory stocks rather than automatically cutting into gross capital formation or working to raise savings through various dynamics. Also, changes in the balance of exports and imports and associated changes in flows in the capital account can change inventory stocks rather than capital formation. Further, a change in gross capital formation, for instance, more investment by destination (IDS) in energy in response to technological change, will lower the stocks in the sector of origin of that capital formation (INVS), but not necessarily quickly change SAVINGS at all. Thus, accounting changes within the financial patterns of any agent category may change savings and/or stocks.
Economies react to inventory imbalances in many ways. There can be changes in prices in sectors affected or across the economy broadly and there can be changes in trade flows as a result of change in domestic prices or the exchange rate. And firms can respond to shortages of inventory stocks by increasing their levels of gross capital formation. That response can have perverse stock shortage effects in the short run because of increasing inventory run down in sectors that are sources of the new capital stock, but also balancing effects because interest rate rises as the firms seek financial capital can shift the decision making of households away from consumption and toward savings. In fact, such a combination of reinforcing and balancing processes is part of the explanation for the oscillation of business cycles.
3.8 Stock SAMS Augment Flow SAMs and Dynamics
Although the traditional SAM matrix represents only annual flows, the temporal dynamics of IFs (discussed in Section 4) require elaborate attention to stocks as well. The IFs system’s interface includes a specialized SAM display that shows both annual flows and a parallel stock matrix that captures the accumulation of assets and liabilities across various agent-classes. The content of that display is both informational and functional. The informational value is somewhat reduced by the relative scarcity of data for initialization of some of the asset and liability stock numbers given the heavy focus by national accounting systems on flows. The preprocessor sometimes estimates stock values by integrating flow information across time (see Supplemental Appendix A). Whether directly data-based or estimated via temporal integration, the stocks shape the feedbacks that influence flows.
3.9 Integration of Partial Equilibrium Models into the General Economic Model
Separate documentation describes the partial equilibrium models for agriculture and energy. It provides some information on the linkages of those models with the general economic model.
3.9.1 Linking the agricultural model to the general equilibrium model
The agriculture model represents production (AGP), consumption, and trade (AGX and AGM) of crops, meat, and fish in million tons. The consumption representation includes food demand (FDEM), as well as feed demand (FEDDEM), food demand for processing/production of food including seeds (FMDEM), and industrial demand (INDEM). The documentation for agriculture as of late 2022 (Rothman, Hughes, Narayan, and Verhagen 2022 in progress) includes a subsection on Economic Linkages that explains variables passed from the agriculture model to the economic model (including gross agricultural production, imports, and exports) and a subsection on Capital Dynamics describing the use of the investment that the economic model calculates can be allocated to the agriculture model, where it is then split between capital stock and land development/maintenance.
Many of the variables that the agriculture model computes for the economic model involve conversion from million metric tons to billion dollars of value. This involves multiplying the physical volumes in each agriculture category (crops, mean, and fish) by the food country-specific price (FPRI) or world agricultural price (WAP) and then summing across the three physical agriculture categories to provide total values for the agricultural sector of the general equilibrium model. The resultant economic model variables are gross production (ZS) from AGP, household food consumption (CS) from FDEM, exports (XS) from AGX, imports (MS) from AGM, investment by destination demand (IDS) from INAG, and inventory stocks (ST) from FSTOCK. The country-specific price variable in the economic model (PRI) is computed from the price of crop variable (FPRI) as a ratio to the world average price (WAP).
With respect to variables from the general economic model that affect or override those in the agriculture model, one key variable is IDS final, which takes into account the demand level passed from the agricultural model (INAG), but reconciles it via normalization with demand in the economic model for investment in other sectors. It is that final IDS variable that feeds capital investment (for land and for production per hectare) in the agriculture model.
Although these linkages between the agriculture model and the full economic model are relatively straightforward, a more complicated issue in the linkage involves representation of intersectoral flows. Section 3.1.1 of this document explained the foundational contributions of the input-output matrix (IO-matrix) to the elaboration of the social accounting matrix (SAM). Within the general equilibrium model of IFs the IO-matrix or A-matrix (AMAT) determines how much of the gross production (ZS) within a sector passes through as production to meet final demand (PFD) as opposed to being intersectoral flows (INTS) used within the production process of other sectors, for instance as crop production of hemp is used in the industrial sector to make rope or cotton is used to make fabric. As that section explained, the intersectoral flows are computed for each column in any production row of the SAM as the product of the gross production in that row and the A-matrix coefficients. The A-matrix itself changes dynamically with values produced by the EIOMat function, responsive to initial data from the GTAP project and changing levels of GDP per capita (with change driven by interpolation among average matrices at increasing levels of GDP per capita). Thus
Given these intersectoral flows (in billion dollars) it is possible to compute the production available for final demand (PFD) as the gross production minus the sum of the intersectoral flows across the columns.
Although very useful, the values from the A-matrix are highly abstract and representative of global patterns, whereas the computations in the agricultural model of intersectoral flows with the variables FMDEM, FEDDEM, and INDEM are much more concrete and initially data-based for each country with respect to the use of agricultural sector gross production by the agricultural sector itself (FMDEM and FEDDEM) or by manufacturing (INDEM).
The differences between the abstract and concrete approaches can be fairly minor in the model’s base year, but they can grow quite dramatically over time. For instance, why should abstract IO matrices for greatly different countries tell us as much about the amount of crop production going to the feeding of animals (FEDDEM) in 50 years as an agricultural model that forecasts the size of livestock herds and that specifies the amount of feed-equivalent available to them from grazing land and therefore the amount needed as supplements from crop production?
Prior to the modeling decision to override that row of the A-matrix with information from the agriculture model, the computations in the general equilibrium model of agricultural production available to meet final demand (PFD) and of change in inventory stocks after directing it to final demand were quite different in future years from the calculations of the agriculture model. Therefore, formulations were built to override the sum of that line of the A-matrix (its top line) with information from the agriculture model. The formulations can nonetheless use the information from the A-matrix to allocate that top row sum to each of the sector-specific columns, because the agriculture model does not suggest how much of the sector’s output is used as intersectoral flow by the energy, materials, manufactures, services, and ICT sectors.
The basic logic of the current formulation has two steps. In the first model year information from the A-matrix is used to compute the sum of intersectoral flows of agricultural production across the agricultural row of the matrix in the base year (iINTSAgSum). That first year’s value of intersectoral flows of agricultural production in the multisector, full equilibrium model is protected and not changed in that base year because it is consistent with the data underlying the entire social accounting matrix.
Also, an initial year computation is made of the ratio of all crop demand to food demand for crops (iAgINTSFlows). The scaling over time of intersectoral flows is tied to crop demand, because the agricultural model has no elaborated representation of intersectoral flows for meat and fish.
In the second procedural step for all years beyond the first, the dollar value of intersectoral flows (INTS) for each cell (column) of the agriculture row is computed using the initial year’s value for the row sum of intersectoral flows multiplied by two ratios. The first ratio scales that initial year row sum by the change in the balance between total crop demand and the demand for crops as food (thus representing the changing need for deliveries to intersectoral flows relative to delivery to final demand). The second ratio allocates the resulting calculation of total intersectoral flows to each sector (column) by using again the additional information about delivery of intersectoral flows to each sector that is available in the multisector equilibrium model.
where
Given the calculation of each cell of intersectoral flows in the agricultural row, now influenced in total by the dynamics of the agriculture model, it is possible to calculate a revised version of that row of the A-matrix (AMATRev).
3.9.2 Linking the energy model to the general equilibrium model
The documentation for the partial equilibrium energy model (Hughes, Solórzano, and Rothman 2023) lays out the linkages between it and the general equilibrium economic model. The variables that move in both directions are fundamentally the same as those that link the agriculture model to the economic model (see Section 3.91), mostly with conversions of physical units in the energy model (billion barrels of oil equivalent or, using the model’s interface, other energy units as desired) to the value units of the general equilibrium model.
The energy documentation includes a section called Economic Linkages. The energy model represents production (ENP) across multiple categories, demand (ENDEM), trade (ENX and ENM), and inventory stocks (ENST). For the general economic model these are converted in the energy model to values for the second (energy) sector, namely ZS, CS, XS, MS, and ST, respectively. Just as with agriculture, the energy model produces a value of demand for investment (INEED) and is given back a value for investment by destination in the energy sector (IDS) from the economic model. And as with agriculture the energy model’s relative price value for energy (ENPRI) is used to change that sector’s price (PRI) in the vector of prices of the economic model.
The primary difference around energy in linkage of the partial and full equilibrium models, in contrast to the linkage of agriculture, is that the demand representation in the energy model does not distinguish between demand for intersectoral flows and that for final demand, implicitly suggesting that the proportions of the two demand categories might be unchanged. There is, however, one important element of reconciliation of the A-matrix structure with information from the energy model. The formulation for that reconciliation is built around the recognition that there has been for a long time (even before the additional impetus provided by concern with climate change) a decreasing use of energy per currency unit of economic activity. That decrease is occurring across all levels of economic development and therefore independent of the logic that links changes in the A-matrix to changes in GDP per capita.
The general equilibrium economic model therefore overlays the more technologically driven changes in energy demand onto the A-matrices that are already responsive to GDP per capita change (the latter produced by the EIOMAT function). It does so by assuming that the A-matrix values for the columns in the energy row change year to year in the same ratio as the overall intensity of energy demand and indicated by its ratio to GDP. This formulation thus assumes that intensity of energy use by other sectors in the intersectoral matrix changes in the same way that intensity of energy use change in final demand (mostly household consumption).
[1] As of this writing the latest update of that was in 2021 by Willem Verhagen on top of an earlier version by Barry Hughes and Mohammod Irfan dating back to 2017 (file named Government Finance Model v6_wv.docx).
[2] The model computes HHTax=HHIncOfficial*HHTaxR, but the actual situation we are trying to represent is HHTax = HHIncFormal* (HHTaxR * X) where X is an implicit factor of increase in the real tax rate so as to represent the application of it only to the formal economy. Some algebra would change the necessary adjustment in the tax rate, but it should not be highly significant relative to other sources of uncertainty.
[3] Useful explanations of the capital and current account components are at https://www.indeed.com/career-advice/career-development/current-account-vs-capital-account https://www.educba.com/current-account-vs-capital-account/ For information on the official reserve account, a subdivision of the capital account, see https://thismatter.com/money/forex/international-balance-of-payments.htm and https://en.wikipedia.org/wiki/Foreign_exchange_reserves
[4] See https://www.sciencedirect.com/topics/economics-econometrics-and-finance/foreign-assets
[5] A useful conceptual overview is in the first chapter of https://www.imf.org/external/np/sta/ir/irprocessweb/pdf/guide2013.pdf
4 Intertemporal Dynamics and Equilibrium
The production function is in many respects the economic model’s foundation in IFs, shaping projections of both the potential for meeting human demands and the pressures the efforts to do so place upon biophysical systems, as well as representing many of the feedbacks from those broader elements of IFs to economics. On top of that foundational element, the social accounting matrix (SAM) provides the basic structure needed to understand key financial flow relationships among households, firms, governments, and countries (or other sociopolitical units) at any given point in time.
Having those two elements in place facilitates further extension of dynamic analysis to issues of equilibrium and disequilibrium across the agent categories that interact within the SAM. In doing so in IFs, we can move well beyond the common representation in economic models of aggregate country equilibration with the simple equation that S – I = X – M. That equation can more accurately and fully be spelled out as national (or domestic) public and private savings minus investment (the sum of gross capital formation and change in inventory stocks) is equal to the current account. While the simple equation often identifies the current account as equivalent to the balance of trade, it also includes net income transfers from abroad and net current transfers (such as remittance and foreign aid flows).[3]
We have seen that IFs extensively elaborates the flows to and among households, firms, and government within and among countries that underly the simple equation. Therefore, it includes accounting representation that allows us to analyze many additional equilibrations, including those specific to government and households and to international actors.
When models give attention to that equilibration of such flows it is often done within each time step. Clearly however, augmenting extensive representation of flows among consumers, firms, and governments, within and across national borders, by also representing the debt and asset stocks to which those flows give rise and which in turn shape the magnitude of the flows across time, is critically important to analyzing dynamically the possible longer-term allocation of resources for addressing social issues. Balancing of flows in the real world to avoid unsustainable build-up in debt (or assets) is temporally dynamic, thereby directing us to the advantage, especially within longer-term models like IFs, of addressing stock imbalances across time.[4]
This section of documentation explains the approach of IFs to representation of such flow and stock representation and relationships, including how the approach facilitates use of the model to explore interventions on both supply and demand sides of the economy in support of a wide range of scenario analyses. The sub-sections of this elaboration (1) juxtapose the IFs approach to dynamic representation, namely a chasing of equilibration across time, with the more common approach involving full achievement of equilibration in each time step, (2) introduce the proportion-integral-differential (PID) methodology used to model that chasing, (3) elaborate the use of the PID methodology in the model across multiple points for equilibration dynamics, and (4) survey some of the model behavior generated by these elements.
4.1 Model Closure: From Exogenous or Static to Dynamic Agency
In addition to “activities” such as production of goods and services and provision of factors such as labor, CGEs built around SAMs represent institutions or agents, namely households, enterprises/firms, governments, and the rest of the world. The SAM represents transfers among these and there are important balances to maintain. Illustrating the approach with a model built within the General Algebraic Modeling System (GAMS), Lofgren, Robinson, and Harris (2002) lay out common features.
An important element in such CGE modeling is the inclusion of rules for “closure” in sub-system structures within each time period. For instance, in factor markets such as labor with demand and supply sides, alternative closure rules can dictate whether wage rates vary so that demand meets an exogenously specified supply or whether wage rates are exogenously fixed, demand responds, and unemployment may result. Moving from an activity to an agent focus, governments obtain revenues and engage in direct consumption and transfers to other institutions (or actors); the resultant government fiscal balance can be designated as net savings. One closure rule of several possible might fix tax rates and expenditures, making savings flexible; another might fix savings (for instance by enforcing balanced budgets) and expenditures, computing tax rates as the balancing term. Similarly, there can be rules that address the tensions in any financial relationship of a sociopolitical entity with the rest of the world, and those rules can look to fixed or flexible exchange rates and/or foreign savings. Further, the society-wide relationship between savings and investment can involve various rule combinations for savings propensity and fixed or flexible capital formation. Referring again to the work of Lofgren, Robinson, and Harris (2002), their Table 3 on page 3 lays out the alternative closure rules that users of the GAMS model can specify in model runs.
The CGE approach to economic modeling using closure rules thus generally assumes that choices need to be made by modelers with respect to which variables in balancing relationships are endogenous and which are exogenous.[5] That approach has much to offer, especially in comparative static analyses, but also in temporally sequential analyses over relatively short horizons. It is less useful in longer-term analysis and especially in longer-term studies in which the analyst seeks to explore multiple possible interventions, including simultaneous ones that might affect both the demand and supply sides of various balancing processes in factor or commodity markets and in the financial exchanges among institutions/agent-actor categories.
In reality, much longer-term economic analysis turns to economic models that are heavily supply-driven and that have limited representation of social accounting and balancing processes. This is generally true with respect to models within the integrated assessment modeling (IAM) community. For instance, that generally characterizes the two models within that community (Crespo Cuaresma 2017 and Dellink, Chateau, Lanzi, and Magné 2017) that made initial contributions of GDP projections across the five Shared Socioeconomic Pathways (O’Neill, et al. 2017). That approach does not even require elaboration of SAMs and closure rules, but rather alternative assumptions about drivers of economic growth. Representation of that growth can serve well as a foundation for analysis of climate change.
Thus, most economic modeling either does not require much attention to both supply and demand sides of modeling or represents one side of economic balances via closure rules. Yet, the increasing movement of the IAM community and other economic modeling efforts into analysis of the broad set of Sustainable Development Goals calls out for acombination of sophisticated supply-side representations with social accounting and with the ability to undertake simultaneous analysis on supply and demand sides within and across various balancing processes that unfold dynamically over time. The IFs system has been structured to address that challenge.
4.1.1 Dynamic equilibrium modeling
Need for that combination has motivated an approach within IFs that can be called recursively dynamic equilibrium modeling. It has several important characteristics, including:
- An explicit differentiation of both stock and flow variables in interaction with explicit representation of multiple demand and supply relationships
- A chasing of demand-supply equilibrium over time (as occurs in the world) rather than representing temporally sequential equilibria
- The use of a dynamic mechanism, based in control theory, called proportional-integral-derivative (PID) or three-term controller
- Resultant model behavior that is influenced by the simultaneous pursuit of multiple equilibria and which is therefore highly complicated across countries and time
With respect to the representation of stocks and flows, a general equilibrium modeling approach with closure rules is almost always focused on flows within single time periods. Even the balance between revenues and expenditures of government is normally treated in terms of a period-specific balancing term, as is the balance of accounts with the rest of the world. In reality, of course, households, firms, governments, and countries run temporally quite variable surpluses or deficits (flows) that accumulate within debt or asset positions (stocks), in the same way that commodity markets have period-specific imbalances that increase or decrease inventory stocks.
It is thus realistic not to insist that all flows be in balance at any given time, but to allow stocks of imbalanced flows to rise and fall, chasing equilibrium across time. Stock levels can be compared with target values that will be specific to various balancing processes, with the deviation from target values providing signals that facilitate flow adjustments on both demand and supply sides in the temporally ongoing chasing of equilibrium.
4.1.2 Algorithmic chasing of equilibrium: The PID controller in IFs
IFs relies on an adjustment methodology for equilibration that is often used in engineering and is called a proportional-integral-derivative (PID) or three-term controller.[6] The adjustment looks at the error or discrepancy of the stock variable from its target level. The proportional term in the controller is the magnitude of that error. The integral term is its sum across time. The derivative term is the year-to-year change in error. For more information on this long-used control structure, see Chang 1961 and Mishkin and Braun 1961. The use in IFs of this mechanism builds upon its earlier implementation by Thomas Shook in the World Integrated Model project (Mesarovic and Pestel 1974a and 1974b).
IFs represents the PID mechanism in a coded function called the adjuster (ADJSTR) that the model calls upon in the multiple equilibrating processes within both the core multisector, currency-value based, dynamic equilibrium economic model and in the physical value-based partial equilibrium agriculture and energy models. Variable and parameter names feeding the ADJSTR function and shown in this subsection are generic and are made specific across IFs applications.
The model first computes a difference (Diff1) between the actual and desired levels for the equilibrium monitoring variable and scales that difference with a scaling base (ScalingBase) value (for instance, total production, demand, or their sum in an economic sector might be reasonable scaling bases against which to gauge the importance of a deviation of inventories from desired levels). In addition, the adjustment mechanism uses a second order difference (Diff2) to compare the error magnitude of the equilibrium monitoring variable with the error in the previous time cycle, relying upon the same scaling base. Nonzero differences result in multiplier values (Mul) that deviate from 1.0 depending also on the magnitude of two elasticities (el1 and el2), and the multipliers are applied cumulatively to the equilibrating flow variable(s). When those flows represent supply and demand and variables contributing to a stock (e.g. annual government revenues and expenditures affecting debt levels), the elasticities for and therefore responsiveness of flows often will differ across the supply and demand sides.
The actual use of the PID ADJSTR function in model code looks like this:
As in engineering applications, the values of the two parameters are tuned to keep error values and oscillation in the system fairly low. Experience has shown that el2 magnitudes are normally about twice as large as those for el1, which often fall into the 0.2 to 0.4 range (with positive or negative signs depending on the application). Hamidian and Jalali (2011) suggest that values tend to be inversely proportional to time delay in response of the system to flow adjustment.[7] Theoretically, the values could be tuned to generate an oscillation consistent with known cycles (such as business cycles or real estate building cycles). Because IFs is a long-term rather than a short-term model, however, we have generally devoted little attention in scaling to the oscillation cycle, focusing instead on long-term stability in the face of shocks introduced by scenarios of model users.
There appears to have been quite limited attention to the applicability of PID control to economic theory, empirics, and modeling. One exception is in thinking about monetary policy. For instance, Hawkins, Speakes, and Hamilton (2014) point out that PID control is a useful extension of the parsimonious Taylor rule (Taylor 1993), which simply says that monetary authorities raise rates when inflation is above a target and lower them when it is below. Similarly, Shepherd, Muñoz Torres, and Saridakis (2019) look at evidence on the fit of monetary policy to PID system behavior and in their abstract say that “the PID rules can provide a useful theoretical and empirical framework …by improving the power of the Taylor rule”. More generally, Carrella (2015) explored the modeling of adaptive economic agents with PID controllers in his dissertation at George Mason University.
4.1.3 PID modeling: Implicitly common in systems dynamic modeling
Figure 4.1 suggests that complexity of behavior with its systems-dynamics style diagram of a much simpler system than the global economy. The temperature in a room (the stock variable) is influenced by two flows, that from a furnace and that from the room to the outside. The magnitude of the flows at any point in time can be represented as the result of two balancing processes (Bs in diagram; also understood as negative or controlling feedback loops) influenced by two target values, namely the thermostat setting and the outside temperature.
We all know that the dynamics controlling the flows in the feedback loops of Figure 4.1 can be quite complex. They will generally involve some acceleration or deacceleration of the flows depending on the magnitude of the gap between the target values and the room temperature stock. Also, sophisticated heating systems will pay attention to the speed of approach to the target and adjust accordingly to minimize overshoot, which may occur anyway as the flow rises or falls in a pattern with some oscillation. Such oscillation in one real-world economic sub-system (e.g. the rise and fall of inventory stocks) will interact with that in other systems (e.g. the rise and fall of government debt).
A major value of the approach in IFs is the ability to look at similar sub-systems individually and in interaction, in the context of analyses focused on either or both supply and demand sides of multiple interacting balance-seeking processes. The IFs model, with its strongly data- and theory-based approach to economic modeling is not a systems dynamics model, but incorporates the stock and flow plus feedback system representations of such modeling.
4.2 Applications of the PID and Recursive Dynamics in IFs
The discussion of the SAM structure in Section 3 included considerable information about the computation of stocks at any given point in time and provided equations showing the use of information fed back from analysis of those stocks to time-specific flows, often in the form of multipliers on those flows. It did not elaborate the computation of disequilibria magnitudes associated with a target level for those stocks or the methodology for generation of the signals back to flows from direct and indirect measures. Those are the purposes of this Section 4.
The discussion in the following subsections identifies two mechanisms that IFs uses to link stock imbalances back to flows, namely direct focus on the imbalances or the computation of indirect imbalance signaling variables. It then continues with a survey of the wide range of applications of the equilibration processes in IFs.
4.2.1 Direct and indirect use of stock imbalances
Several important uses of PID control in IFs involve balances that CGEs often address with exogenous closure specifications and for which IFs uses stock levels relative to a target value to affect flows directly. An example is the use of government debt (GOVDEBDT) as a percentage of GDP to affect both government revenues (GOVREV) and expenditures (GOVEXP). Other more indirect uses of the PID controller first compute a price variable that then affects flows. Price variables include the price (PRI) of goods and services in domestic commodity markets, interest rates (INTR), the exchange rate (EXRATE) of national currency, and a wage index relative to GDP per capita (LABWAGEIND).
In some cases, the computational sequence of variables in each year makes it more efficient (e.g., more immediate with less lag) to use the stock level imbalances directly to influence flows rather than using the computed changes in prices. For instance, the economic model uses sectoral economic stocks (ST) from the previous year (SST) to directly affect the flow of investment into the sectors of destination (IDS) rather than using relative prices by sector (PRI). Similarly, in the agricultural model food stocks (FSTOCK) carried from the previous year directly affect yield levels (YL).
4.2.2 The full set of PID applications in IFs
The following subsections of Section 4 elaborate equilibrating dynamics. Discussion of creating price-related indices to aid in equilibration (Section 4.3) will elaborate the following:
- Using inventory stocks (ST) relative to targeted levels to affect sectoral prices (PRI). That PID uses the parameterselprst1 and elprst2.
- Using external debt (XDEBTRPA) to affect exchange rates (EXRATE); uses elerca1 and elerca2.
- Using inventory stocks (ST) relative to targeted levels again to compute interest rates (INTR). The calculation uses a modified PID focusing only on absolute annual difference between actual and targeted stocks and not also the change in that difference over time (a P rather than PD controller). Further, for feedback purposes in the broader system INTR is used in the calculation of a smoothed value of the interest rate (SmoothIntR) and an even more smoothed long-term value (LongTermIntr)
- Not discussed in Section 4.3 but relevant to firm-influenced equilibration and discussed in Section 6 are:
- Using unemployment relative to a target level to compute LABWAGEIND
- Using LABWAGEIND (when labmarketsw=1) to affect LABDEMS (labor demand by sector and skill level)
With respect to computations of flow variables that either use the above indices as drivers or look to underlying imbalances directly, it is possible to roughly divide them into variable categories corresponding to agent categories, namely firms, households, and governments. Several are specially related to firms (but more generally to markets in which households and governments are also key actors):
- Using inventory stocks (ST) relative to targeted levels to affect capacity utilization (CAPUT) in the production function. That PID uses hard-coded 0.1 and 0.2.
- Using differences between world prices (WP) and domestic prices (PRI) times the exchange rate (EXRATE) modified by tariffs (TariffTaxR) to adjust rates of sectoral exports (XS) and imports (MS).
- Using the smoothed and long-term interest rate values to compute one of the factors that determines the share of gross capital formation (IGCF) in potential GDP (GDPPOT). That PID uses parameters that are a combination of hard-coded values (0.4 and 0.6) and computation with decreasing values as GDP per capita rises.
- Using inventory stocks (ST) to allocate gross capital formation (IGCF) to destination sectors of investment (IDS); the PID uses elinst1 and elinst2
With respect to household flows (Section 3.3 documents the use of the resultant multipliers) we will discuss in particular:
- Using the cumulative savings stocks of households (HHSAVSTOCK) relative to a calculation of retirement (pension) needs (HHSAVNEEDSTOCK) to compute a surplus or deficit in those savings (HHSAVSURSTOCK) and affect the consumption ratio or share (CRa) of household income (C) by household type via hard-coded PID parameters of 0.1 and 0.2.
- Using also a smoothed value of the interest rate (SmoothIntR) to affect the consumption ratio or share (CRa) of household income (and therefore also household savings)
- Using household and firm savings rates (HHSAV and FIRMSAV) relative to a long-term target value to further affect household consumption (C)
- Using excess stocks directly to affect household consumption
With respect to government (Section 3.4 documents the use of the resultant multipliers) we will look at:
- Using government debt absolute (GovDebtAbs), which accumulates government balances (GOVBAL) over time, to affect revenues (GOVREV) and thus taxes as well as expenditures (GOVEXP), both transfers and direct consumption. Uses elgrevdebt1 and elgrevdebt2 for revenues and elgexpdebt1 and elexpdebt2 for expenditures.
Although the focus of equilibration discussion in this document is on the currency-based general equilibrium-seeking model, we should note that other models in the IFs system also use the PID-based approach, including in the partial equilibrium agriculture and energy models:
Uses of PID in the partial equilibrium agriculture model:
- Use world food stocks (FSTOCK summed) to affect growth in agricultural technology contribution to yield (TechContrib), thus the level of that technology (AGTEC), and then yield YL). Using elfdpr1 and elfdpr2.
- Using also regional food stocks (FSTOCK) to directly affect yield (YL). Also using elfdpr1 and elfdpr2.
- Using regional food crop stocks (FSTOCK, accumulated as CumStk) to affect crop prices, changes in the smoothed values of which pass to meat price change. Uses fpricr1 and fpricr2.
- Using global fish stocks (WCumStkBalanceFish) to affect global fish price (WAP for category three). Uses fprimt1*2.5 and fprimt2*2.5); assigning global fish price to each region.
- Using regional food crop stocks (FSTOCK) in crops to affect demand for investment in agriculture (INAG). The meat version of the multiplier affects growth in the livestock herd. Uses hard coded -0.1 and -0.3.
- Using also world food crop stocks (*FSTOCK summed) to affect targeted investment level (INAG). Uses hard coded -0.1 and -0.3.
- Using world meat food stocks (FSTOCK summed) to affect the growth of the global livestock herd (WLvHerd), which then affects national herd sizes. Uses hard coded -0.15 and -0.3.
- Using return to land (RETLD) as a portion of total return to capital (producing RETRAT) to affect investment in land share (IALK) of total agricultural investment available (IAval). Uses eliasp1 and eliasp2.
Uses of PID in the partial equilibrium energy model:
- Using both world and regional energy stocks (WEnStks and ENST) to affect regional energy prices (ENPRI). World using hard coded -0.2*3 and – 0.4*3. Regional uses epra and eprafs.
- Using regional energy stocks (ENST) to affect capacity utilization (CpUtF). Uses elenpst and elenpst2.
- Using exchange rate (EXRATE) to affect energy exports (ENX). Uses hard-coded -0.2 and -0.4.
- Using a decreasing (converging to 0) target for energy import rate (MkAve) to affect that import rate. Uses hard coded -0.1 and -0.2.
- Using world energy stocks (WEnStks) and domestic energy profits (EPROFITR) to affect demand for investment in energy (TINeed), to take to the economic model and IDS.
Uses of PID in the equilibrium-seeking water model:
- Using the demand/supply ratio for water (DemandSupplyRatioWater) to affect water price (WATPRICE). Uses watprii and watprid.
- Using water price (WATPRICE) to affect desalination level (WATERDELSALINATED). Uses desali and desald.
4.3 Determination of Indices that Influence Flow Variables
Inventory stocks (ST) are a key variable in the equilibration processes of IFs, sometimes used directly as a basis for signals to various flow variables and often used indirectly via variables such as relative prices (PRI) and capacity utilization (CAPUT) in economic sectors. Further, they interact with and influence changes in exchange rates (EXRATE) and interest rates (INTR).
The reason in inventory stocks take on such an important role is that changes in them are influenced very directly by household, firm, government, and international agency. Within a recursively dynamic general equilibrium model (GEM) such as IFs, inventory stocks serve as a temporary buffer between fundamentally all drivers of demand and supply. The production available for final demand (PFD) serves to increase stocks (see the documentation in Section 3.1.1 of gross production, assumed meeting of demand for intersectoral flows, and computing production for final demand as a residual). Various subsections within Section 3 discussed the agency that gives rise to sectoral household consumption (CS), investment by origin sector (INVS), and government spending (GS) by sector of origin, as well to sectoral imports (MS) and exports (XS). Together these terms augment or decrease inventory stocks over time.
The three subsections that follow explain how the inventory stocks generate change over time in three “pricing” or indirect signaling variables, namely relative sectoral prices (PRI), interest rates (INTR), and capacity utilization (CAPUT). The fourth subsection turns to exchange rates (EXRATE).
4.3.1 Domestic price dynamics across economic sectors
Prices in IFs (PRI) are relative “real” prices across time and sectors and are indices around initial base values of 1.0 In the partial equilibrium agriculture and energy models the prices (FPRI and ENPRI) have very similar computational structure. Prices are changed over time by a multiplier (Mul) that is responsive to inventory stocks (ST) relative to a target value (the Diff1 term) via the ADJSTR function within the PID process. Prices also respond to changes in level of those stocks; the Diff2 term increases the previous year’s inventory stock by the corrected initial GDP growth rate (igdpcor) so as to make it comparable in size to the inventory of the current year.
The stock base (STBASE) provided to the ADJSTR function for scaling of the stock level and the change in it is the sum of two terms. The first is gross production (ZSP), which is important to large producer countries in an economic sector, whether they consume domestically or export. And it includes initial year imports (MS) scaled up by potential GDP growth over time. The import term is important to large importers, when domestic production is small (and use of a version of the initial year import level scaled by potential GDP (GDPPOT) growth over time introduces stability relative to use of potentially more volatile annual imports). Potential GDP is also used to provide some stability for the equilibration process in the face of the more volatile GDP calculation; in the base year GDP and GDPPOT are identical. The desired level of stocks as a portion of the base (dstl) is exogenous.
The forward impacts of prices (PRI) are primarily through trade and secondarily through price-responsiveness of sector-specific consumption. In addition, prices implicitly affect investment by destination, although for reasons of computational sequence IFs uses stock levels directly to direct investment by sector. Section 4.4 returns to these forward impacts.
4.3.2 Interest rate dynamics
Brzoza-Brzezina and Crespo Cuaresma (2007: especially pages 3 and 7) draw attention to literature and their own analysis showing the importance for interest rates of demographic structure including dependency ratio, government deficits, international factors including capital flow liberalizations that affect the current account, and the savings rate. Lane (2019) drew attention again to demographic change (notably aging global populations) and also to income distribution with its effect on savings. Earlier, Orr, Edey, and Kennedy (1995) looked at the impact of increased government deficits on interest rates.
Such literature on determinants of interest rates, generally focusing on deep or distal drivers, does not focus on more immediate or proximate ones such as changes in inventory stocks relative to desired levels. Yet those more distal drivers identified as influencing change in rates are clearly related to the tightness of the economy in physical and financial terms. Being influenced by so many of the identified factors (which cut across the agency of households, firms, governments, and international actors), inventory stocks are a clear and strong indicator of that agency and the economic balance or imbalance to which the agents gives rise.
IFs does not maintain a monetary sector that would introduce nominal interest rates (or nominal prices) so the focus is on real rates. IFs uses a simplified PID controller (looking only at the absolute difference in desired stocks from target values and not at the annual change in that difference) in computing the real long-term interest rate (INTR).
Further, it computes interest rates as responsive to the average of two terms. The first term anchors interest rates relative to a stylized long-term real interest rate equal to the long-term economic growth of the country (igdpr) computed in the preprocessor (and put into the base year value of the interest rate). On a global basis that roughly equals 3 percent. The term adds to that anchor a ratio of the gap between desired and actual inventory levels to the desired level (implicitly the same as the P (proportional) term in the PID controller); the impact of stock variation from the target level has been tuned with a factor of 2. The desired stocks are a product of the desired stock level rate parameter (dstl) times a stock base (STBase) that is a sum of gross sectoral production (ZS) and imports (MS) modified from the first year by GDP growth – that stock base can serve both countries that produce most of what they need domestically and those that need import much of what they need.
That first term in the equation below (the initial stylized rate plus a representation of the variation in the stock levels from the target) is then averaged with the interest rate in the preceding year. See previous subsection documentation on changes in relative prices for more information on the stock base and the general approach. Resultant interest rates appropriately rise as stocks fall relative to desired levels and fall as stocks rise above those desired levels.
An additional step in the process limits the absolute value of the interest rate to keep it between 0.01 percent and four times the initial year’s value. And a final step limits any annual increase to 80% of the previous year’s value. These constraints keep the interest rate from having extreme values in a model where interest rates are long-term and real rather than nominal (again, IFs has no representation of inflation). Such limiting stands in contrast to the more volatile short-term changes in exchange rates and to the more volatile behavior of interest rates often driven by complex combinations of monetary and fiscal policy that the model does not represent. Nonetheless, given various international and domestic structural imbalances that can appear in the IFs base case and scenarios, interest rates can change quite dramatically over long-periods of time.
Even with the smoothing of interest rate calculation via the use of the initial year interest rate anchor, the averaging with the previous year, and limitations placed on annual changes, a model of long-term behavior like IFs benefits from some further smoothing of the interest rates before they feed into their impacts on consumption and investment patterns―that helps represent the slowness of response in persistent patterns exhibited by households and other agents to changes in interest rates. Two smoothed terms (a very long-term interest rate, LongTermIntr, and a smoothed rate, SmoothedIntr) moderate further the impacts of ongoing variation in real interest rates; thus, IFs is focused on long-term behavior of response in consumption and investment to interest rates.
Just as changes in real relative prices by sector help the goods and services market chase equilibrium across time (using build-up or run-down of stocks or inventories to change prices and send signals to supply and demand sides of the model), changes in interest rates (INTR) send signals to consumption and investment, facilitating the system’s chasing of equilibrium between savings and investment over time. For example, a subsequent sub-section (4.4.2.2) will explain the impact that these interest rate terms have on the trade-offs that households make between directing disposable income to either consumption or savings.
4.3.3 Capacity utilization dynamics
The discussion of the goods and services market emphasized the importance of the production function given the critical role of the supply side of the economy in long-term forecasting (Section 2.2). One of the terms in the Cobb-Douglas production function is sector-specific capacity utilization (CAPUT). It is changed over time by a multiplier (Mul) that is responsive to inventory stocks (ST) in a use of the ADJSTR function that represents the PID process’s responsiveness to level of those stocks and their change over time, adjusting the previous year’s inventory stock by the corrected initial GDP growth rate (igdpcor), to make appropriate comparison to the inventory of the current year.
The stock base (STBASE) provided to the ADJSTR function for scaling of the stock level and the change in it is the sum of two terms. The first is gross production (ZSP), which is important to large producers, whether they consume domestically or export. And it includes initial year imports (MS) scaled up by potential GDP growth over time. The import term is important to large importers, when domestic production is small (and use of a version of the initial year import level scaled by potential GDP (GDPPOT) growth over time introduces stability relative to use of potentially more volatile annual imports). Potential GDP also enhances stability within the equilibration process in the face of the more volatile GDP calculation. The desired level of stocks as a portion of the base (dstl) is exogenous.
4.3.4 Exchange rate dynamics
Another PID computation determines exchange rates, effectively another price index term. The real exchange rate is the most direct instrument of international account equilibration, responsive to the ongoing balance between current and capital accounts as represented in changes in official reserves and broader international debt. This is especially true for emerging markets where adequacy of such reserves for day-to-day transactions and serving as lender of last resort (in the case of currency crises) are critical (Green and Torgerson 2007). This therefore has suggested to analysts the utility of at least rough targets for the stock of those reserves held by the government. For instance, the Greenspan-Guidotti rule suggests that reserves should equal all external debt coming due across the coming year and, given the risk of capital flight, another benchmark is that reserves should be 5-20 percent of M2 (Green and Torgerson 2007:3). Such rough rules suggest also very crude guidelines for relatively near-term change in exchange rates over time.
With its focus on long-term forecasting and absence of any representation of money supply or strong representation of foreign reserves, the IFs system looks to international debt as a portion of GDP as a driving variable for change in the exchange rate. The process has two steps: (1) the determination of a debt (net of assets) level as a portion of GDP to serve as a target value for international debt; (2) using the PID algorithm to change the country’s exchange rate to push the external debt variable toward the target ratio of GDP.
Historically high and very persistent international debt to GDP ratios of countries like Namibia and Micronesia, combined with long-term high net international asset ratios of countries like Brunei, Kuwait, and Luxembourg, suggest that such imbalances might not greatly influence underlying patterns of change in the exchange rates and equilibration-driven movement to any common target for debt or asset ratios to GDP across those countries.
In fact, this suggests that there is no simple universal, and especially near-term target level for international debt or assets as a ratio of GDP. Modeling in IFs has experimented with the calculation of a TypicalDebt ratio variable as a function of GDP per capita at PPP, but resultant values often lie far from current and sometimes persistent past values. Another potential approach explored is to simply use the base year ratio of international debt or asset to GDP as the long-term target. Yet, indefinite maintenance of very high debt or asset to GDP ratios also seems improbable and is contrary to historical experience.
Following such efforts, which tended to generate unlikely patterns in forecasts across the century, the currently implemented approach is to make the debt-asset ratio to GDP target (XDebtTargetPerGDP) a value that converges from the initial base year value (XDebtIRat) to zero over the very long horizon of 200 years. This is very different than the equilibration logics around sectoral prices, interest rates, and capacity utilization where a universal ratio of inventory stocks to the stock base is used as a target value across all countries and time points.
IFs does not represent alternative exchange rate regimes (e.g., fixed or floating exchange rates) and models all national exchange rates as effectively floating over time. Given the moving target value, the exchange rate index in IFs (EXRATE) responds over time to the gap between the slowly moving target and the changing ratio of external relative price adjusted debt level (XDEBTRPA) to potential GDP (GDPPOT).
The exchange rates change with a multiplier (Mul) computed in the PID’s ADJSTR function, controlling movement from each year’s debt level as a portion of GDP toward equilibrium by using both the absolute difference of the debt ratio relative to the target value (Diff1) and the change in that debt ratio from the previous year (Diff2).
The parameters used in the exchange rate adjustment above are second-order parameters computed from exogenous specifications (elerca1, elerca2). Recognizing that high ratios of debt to GDP are less sustainable that are high lower ratios or even high ratios of net assets to GDP, for countries with ratios of debt to GDP above 1 the adjustment process described above is accelerated by increasing both parameters in the PID function (some extra weight is given to the parameter of the year-to-year term).
Even with exploration of several alternative formulations, long-term behavior of the exchange rate system has been challenging to represent. It may be one area of the model where additional refinement will be ongoing.
4.4 Determination of Flow Variables from Indices or Directly from Imbalances
This section continues the documentation of formulations underlying intertemporal dynamics and equilibration in IFs. Earlier sections have explained the general PID equilibration process, outlined where it is used in IFs, and distinguished between its use (1) to directly generate changes in flows from stock imbalance and (2) to compute indicator or price variables that mediate between those stock imbalances and changes in flows. The sub-sections below move to detailing the adjustment processes most closely related in turn to firm, household, government, and international agents that are driven by those stock imbalances or price variables.
4.4.1.1 Gross capital formation and investment
Firms are substantially in control of the investment variable known as gross capital formation (IGCF) and its targeting across economic sectors (IDS). The equation below indicates that the core of the gross capital formation (IGCFCore) calculation each year is potential GDP (GDPPOT) times an investment rate (IRA) from the initial year. The investment rate core determination also involves input from net inward foreign direct investment flows (XFDIFIN – XFDIFOUT) and portfolio flows (XPORTFIN-XPORTFOUT) as a ratio to relative price adjusted GDP potential (GDPPOTRPA); not all financial outflows decrease domestic investment and xfdioutf represents the reduction in local capital formation for each dollar of FDI outflow (the default value is 0.5).
There are multiple factors that modify that core (generating IGCFModified). (See in Section 3.3 the similarities in the calculation of household consumption as having a core in permanent income, with a number of factors modifying it.) In general, those modifications help investment react both indirectly (via interest rates) and directly to changes in inventory stock patterns and they help maintain the equilibrium of the domestic economy.
The first adjustment factor is an interest rate multiplier term (IntrMulTerm or IRaMul in the code) that, like the one on consumption, drives down investment when interest rates rise (the annual change in the multiplier, Mul, reinforces change impact). In fact, the multiplier responds to smoothed and long-term interest rates exactly as consumption responds, although the parameters in the PID adjustment or ADJSTR function (IPar1 and IPar2) make the adjustment a little less responsive. In contrast to most PID function parameters, which have identical values for all countries, IPar1 and IPar2 are hard-coded with basic values of 0.4 and 0.6, divided by a term that decreases their responsiveness to the Diff1 and Diff2 terms as GDP per capita at PPP rises.
The next adjustment factor is a direct response to excess stocks or inventories. Again, this is parallel to the adjustment of household consumption to stocks, except that 1/2 of the excess stocks are passed to household consumption and only 1/8 of them are assigned to gross capital formation.
Additionally, there are two adjustments that reflect the changing life expectancy and related savings patterns of the society. The first (LifExpGap) reacts to changes over time in the variation of the actual life expectancy (LIFEXP) from the life expectancy expected given the GDP per capita at PPP of a society (LifExpComp). If the gap increases, a small portion of it increases investment rates (as it would savings rates). The second again involves life expectancy, but the purpose of it is to reflect the changing age structure of a society and the consumption/savings-investment patterns of societies with different age structures. Finally, an exogenous multiplier (invm) allows the user to push capital formation rates up or down.
Gross capital formation, although highly correlated with investment (I) is not equal to it. Investment also contains changes in inventory stocks. It is that addition of delta stocks that brings the entire representation of the goods and services market into proper relationship with the financial representations of flows among agent classes.
Having gross capital formation, it is also possible to compute investment by origin sector (INVS); in the absence of useful data, the preprocessor assigns all investment by origin to the manufacturing and service sectors. In IFs, the base year allocation of origin is constant over time.
The direction of gross capital formation to sectors of destination is, however, a more complex process that the next subsection explains.
4.4.1.2 Investment by destination and capital stock
The determination of investment by destination is a two-step procedure. First, IFs computes demand for investment by each sector (IDSDem), responsive primarily to inventory levels (ST) carried into a given year from the previous one as saved stocks (SST). The base value of sectoral investment demand is significantly dependent on the total level of gross capital formation (IGCF) and the portion of that directed into a particular sector (IDK) during the last time step. On top of that, values of inventory stocks relative to target levels and their change over time shifts investment across sectors. Parameters (elinst1 and elinst2) control the speed of that shift via PID adjustment (ADJSTR).
The above equation handles the sectors other than agriculture and energy. The model for agriculture provides investment need for that sector (IANEED), as does the energy model for its sector (IENEED). The code puts ceilings on the values coming from the partial equilibrium models so that they do not take all the available capital formation value.
To obtain actual investment by destination (IDS) we can distribute total gross capital formation (IGCF) across sectors proportionately to their demands.
As an indicator (and as the basis for sectoral investment splits in the next time cycle) we compute the fractions going to each sector (IDK).
Capital stock (KS) for the next time period is simply the current year’s capital stock plus investment by destination, minus depreciation (the capital stock divided by its lifetime, lks), and minus the portion of capital destroyed as civilian damage (CIVDM) in war (see the policy model). The last term is non-zero only in very specialized scenarios.
IFs makes no effort to represent a gestation period for capital of more than 1 year. Although it would be desirable to do so, it would also require a "look ahead" capability of the model to plan capital requirements several years in the future. Such a feature would add some realistic cyclical behavior to the model, but would also be somewhat difficult to control. And it is not the aim of IFs to capture business cycles. Similarly, IFs does not maintain age cohorts of capital stock so as to potentially refine its depreciation over time.
As described in Section 3.3, four equilibration dynamics to be elaborated in the following sub-subsections shape the shares of household disposable income directed at consumption and savings. The first of these relates directly to the demographic logic of households and their potential savings needs for retirement. This logic is most important for countries with greater life expectancy and higher incomes, which motivate and facilitate attention to potential savings for retirement (and often medical) needs. That logic computes the internal variable HHSavSurStockMul.
The next three household-related dynamics are used in the SAM logic as explained in Section 3.3.4. The second equilibration dynamic is driven by the interest rate (INTR), specifically by its smoothed value (SmoothIntr). That logic computes an interest rate multiplier term for consumption (IntrMulTermC).
The third dynamic is household reaction to prices of potential consumer goods. As the subsection below explains, however, computational sequence makes it appropriate to substitute inventory stocks (themselves the driver of prices) for use of the price variable. It does not compute a multiplier but rather uses ExcessStocks directly to modify consumption.
The fourth dynamic related to household use of disposable income is an equilibrating factor that recognizes the reality that over the long-run and across countries, domestic savings as a ratio to GDP tend to fall into a fairly narrow range. It thus computes another multiplier for consumption (MulCon) that helps the model tend toward the center of that range.
4.4.2.1 Savings stocks versus savings needs
Section 3 identified two adjustments to an initial basic calculation of household consumption (C) driven by GDP size in interaction with the dynamics of changing age structure and propensities for consumption across that structure. The first adjustment involves an equilibration process of accumulated household saving stocks with estimated savings needs in retirement given a specified retirement age but changing demographic structure. The second adjustment is responsive to changing retirement ages (sometimes driven by scenario analysis) and is done in the code via an additive factor (AgingAdjustment) as explained earlier in Section 3.3.3.
The first equilibrating adjustment is the focus here. Households, particularly in countries where the incomes are high enough and the life expectancy long enough, will shape their consumption share of income at least in part with eyes toward financial needs in retirement years. In IFs, that is represented via an equilibration process comparing on-going calculations of saving stocks (HHSAVSTOCK) with those for estimated savings needs in retirement (HHSAVNEEDSTOCK). This sub-section explains the calculation of these two variables and then their use via equilibration to compute a multiplier (HHSavSurStockMul) for adjusting annual consumption values (and implicitly savings values as a residual that is computed subsequently). Section 3.3.2 showed the use of that multiplier.
It is possible to calculate the accumulated stock of savings (HHSAVSTOCK) by augmenting it across years with an expected investment return rate parameter (savingsdiscountrt), adding new savings (HHSAV), and subtracting each year’s use of savings (HHSAVUSE). The use of household savings depends on the consumption needs of retirees (CRETIRE) computed in the initial determination of total consumption levels (Section 3.3.3.1), minus the portion of those needs provided by government pensions (GOVHHPENT). IFs does not yet differentiate stocks of savings by household type.
An estimate of the ultimate needed stock of savings (HHSAVNEEDSTOCK) depends on the annual use by retirees of the stock (HHSAVNEEDUSE), in turn the difference between the annual total need of retirees (HHRETIRENEED) and the portion of that need covered by government pensions (GOVHHPENT). The computed value for annual retirement consumption needs is multiplied by a parameter that is by default 1 but can adjust that consumption value for scenario use (retireconsumrat). Under the assumption that the stock to generate the annual need depends upon a return to the stock determined by the savings discount rate (savingsdiscountrt), the stock needed is the annual use of the stock divided by that rate.
Comparing the actual accumulated stock with the stock needed generates the surplus (or very often deficit) in household saving stocks (HHSAVSURSTOCK).
The target value for HHSAVSURSTOCK in the equilibration process is zero. The calculation of the multiplier on consumption (HHSavSurStockMul) in pursuit of that target uses the ADJSTR function, which Section 4.1.2 explains. That PID function requires the specification of a scaling term, in this case GDP. It uses two difference terms. The absolute difference from the target (Diff1) is the surplus or deficit of savings itself, lagged one year because of computational sequence. The Diff2 term is the change in that surplus or deficit between last year and the year before. Each difference term is divided by 25 because it is recognized that an equilibration involving savings and need for them would unfold only over much time. The function also requires scaling parameters for the two difference terms, hard-coded as 0.1 and 0.2.
Section 3.3.2 explained the use of the resultant multiplier in computing a basic or preliminary value of household consumption:
=====
- ↑ Much documentation of IFs precisely follows the code and places the names of many variables on both sides of equations shown. In much documentation of models in literature, however, that practice is eschewed and care is taken to recognize that variables included on the right side of the equal sign are different in value than the same variable by name on the left side of the equal sign. In this document the practice is somewhat mixed, but where the common IFs documentation practice could be especially confusing, variable names like VADDPrev are used on the right-hand side even though they do not exist in the code itself. When that is done they will typically be shown in mixed upper and lower case.
- ↑ A good elaboration of many of these is by Stephanie Glen: "Fixed Effects / Random Effects / Mixed Models and Omitted Variable Bias" at StatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/experimental-design/fixed-effects-random-mixed-omitted-variable-bias/ See also https://machinelearningmastery.com/model-residual-errors-correct-time-series-forecasts-python/ and https://otexts.com/fpp3/ e.g. section 5.4, 13.9.
- ↑ See an IMF elaboration of the concepts at https://www.imf.org/external/pubs/ft/fandd/basics/current.htm by Atish Ghosh and Uma Ramakrishnan, “Current Account Deficits: Is There a Problem?” See also the publication by the Boston Federal Reserve Bank at https://www.bostonfed.org/-/media/Documents/neer/neer400a.pdf
- ↑ In addition to being observationally obvious, Kornai (1971) and others have argued that real world economic systems are not in exact equilibrium at any time point, despite the convenience of such assumptions for much economic analysis. In contrast, the SARUM global model (Systems Analysis Research Unit 1977) and GLOBUS (Hughes 1987) used buffer systems similar to that of IFs with the model "chasing" equilibrium over time.
- ↑ A power-point presentation by John Gilbert explicitly emphasizes this point and lays out closure rule approaches in CGEs, see https://artnet.unescap.org/tid/artnet/mtg/cge13-closure.pdf.
- ↑ See https://en.wikipedia.org/wiki/PID_controller. Wikipedia explains that the P is current value of the error, I is integrated error over time, and D is based on the current rate of error change. IFs works with stock levels relative to target values as proportions of a scaling term in most of its balancing systems; doing so inherently involves both the I and P terms. IFs also looks at the change in that error across time periods, the D term. Some applications in IFs focus more on flows. Many PID applications are applied directly to flow analysis, like the Wikipedia example given around cruise control in vehicles while hill climbing versus flat or descent situations. Use of a PD subset (and also of a PI subset) is described at https://eng.libretexts.org/Bookshelves/Industrial_and_Systems_Engineering/Book%3A_Introduction_to_Control_Systems_(Iqbal)/03%3A_Feedback_Control_System_Models/3.3%3A_PI%2C_PD%2C_and_PID_Controllers. See also https://eng.libretexts.org/Bookshelves/Industrial_and_Systems_Engineering/Book%3A_Introduction_to_Control_Systems_(Iqbal)/03%3A_Feedback_Control_System_Models/3.3%3A_PI%2C_PD%2C_and_PID_Controllers
- ↑ On page 3 of this they talk about a PI0.4D0.7 controller. Note both the use of exponents and the roughly 1-2 ratio of the parameters. In general the literature talks about tuning the controller experimentally. And about PID as being the dominant or work-horse approach in the control literature.
4.4.2.2 Interest rates and consumption
Although the division of household disposable income into consumption and savings shares is driven heavily by income levels and demographics, interest rates also affect it. The impact of interest rates on the consumption level and share (leaving savings to be the residual) is introduced via an interest rate multiplier term (IntrMulTermC) that rises or falls over time as a function of the difference between a smoothed interest rate term (SmoothIntr) and a very long-term or highly-smoothed interest rate term (LongTermIntr). That is, as the smoothed interest rate rises above the long-term interest rate, it depresses consumption (and will therefore raise savings). In IFs there is no monetary sector and interest rates are real rates, not nominal ones.
The ADJSTR function of IFs computes the multiplier using its PID logic. Although the basic parameters of the function are hard coded as 0.9 and 1.8 at very low levels of GDP per capita at purchasing power (GDPPCP), the parameters decline with rises of GDPPCP given the tendency for interest rates and consumption share of GDP both to be somewhat less volatile at higher levels of it. As is common with use of the PID logic, there are significant elements of tuning and judgment involved in its calibration.
Section 3.3.4 discusses this equation for revision of household consumption in which the multiplier is used:
4.4.2.3 Excess stock additive term (proxy for price changes)
Although interest rates respond to inventory stocks above or below the target value for them and pass on that disequilibrium to household decisions about division of income between consumption and savings, that division of income by households responds even more to changes in prices of goods and services. Therefore, the implications of price changes should augment the implications of demographics and interest rates in the model’s formulations. In IFs, relative real sectoral prices respond to inventory stocks, but given computational sequencing in the recursive model structure, changes in prices lag a year behind changes in inventories. Thus, the formulation for representing price effects looks directly at inventories.
Excess stocks (ExcessStocks) are the difference between actual (ST) and desired stocks, the latter being determined by a stock base (STBase) linked to production and consumption levels and a desired stock level parameter (dstl) as a portion of the stock base. As indicated by the equation at the end of the sub-subsection just above, the fraction of the excess passed through to consumption adjustment is ¼ (and limited in the code to no more than 15% of the GDP). The fraction was set based on behavioral analysis and may well be adjusted with continued model use.
4.4.2.4 Consumption adjustment for movement to target savings rate
On a global basis savings and investment should be equal, an identity well understood in economic modeling (elaborated in Section 4.5). In the 2017 base year of IFs version 7.94, the global rate of those variables as a percentage of GDP was 25 percent, a value that tends to slowly rise with GDP per capita―it is not unreasonable to anticipate that it may reach 30 percent globally by century end.[1] Thus, in spite of the responsiveness of households to variables such as interest rates and inventory stocks in their division of income into consumption and savings, the IFs system overall should recognize this long-term pattern. It does so in the computation of a final adjustment to household consumption via a multiplier (MulCon) that we have seen in Sections 3.3.4 and 4.4.2.1 to be used in the equation for the final computation of it.
IFs compares total national savings by households and firms as a portion to GDP (HHFIRMSavR) with a target level for such savings (HHFirmSavTarget) that convergences (using the function ConvergeOverTime) from initial year values to 30 percent. It uses the standard IFs PID adjuster function (ADJSTR) to compute the equilibrating adjustment to consumption (MulCon). Later code computes household savings as a residual of household disposable income and consumption.
Foreign savings actually augment savings by households and firms. It is therefore possible that they can dramatically influence national savings totals relative to domestic savings and in some countries they do and therefore could be used in the formulation above. Over the century-long horizon of IFs, however, it is unlikely that many countries will persist in having large inflows or outflows of savings, reinforcing the likelihood of movement of domestic savings toward the common target. Nonetheless, foreign savings computations with or without scenario intervention can still shift the total national savings away from the target.
4.4.3 Government debt and revenue-expenditure dynamics
Given calculations of government revenue (GOVREV) and expenditure (GOVEXP) as documented in discussion of the SAM structure, it is possible to compute the government balance (GOVBAL). That balance does not just reflect domestic finance, because government revenues include foreign aid sent or received, government expenditures include direct consumption enhancements from World Bank inflows, etc.
The balance allows update of absolute government debt (GovDebtAbs) and a calculation of its magnitude as a percentage of GDP (GOVDEBT). We use the relative price adjusted GDP (GDPRPA) because it reflects changes in energy and agricultural prices that can be of considerable significance for the government finance of countries with heavy dependence on trade in those sectors. When AID is positive indicating net receipts, the loan portion of the aid as indicated by a parameter (aidlp) is also added to government debt in the equation below.
It is government debt as a percentage of potential relative price adjusted GDP that IFs uses to build equilibrating dynamics for government revenues and expenditures. In years beyond the first, that percentage will give rise to pressure for higher or lower levels of government revenues and expenditures. Those pressures are conveyed via two multipliers applied to calculations of taxing and spending in subsequent years. Those multipliers are set at "1" in the first year, indicating no change in pressures initially. The rest of this subsection explains how those multipliers are changed over time.
The first step in feeding back government debt level to pressures for increases or decreases in revenues and expenditures is to specify a target for government debt as a percent of GDP with which to compare the actual level. This is a much more complicated process than with inventory stocks of goods, simply because while there clearly are at least subjective limits to and targets around government debt levels, there is no theoretical, empirical, or sociopolitical consensus on the issue: actual values across countries and over time vary greatly.
A cross-sectionally estimated function relating levels of debt to GDP per capita at purchasing power parity (GDPPCP) is used as the foundation in IFs for specifying that target ratio of government debt to GDP (GovDebtComp). Dynamically, the target determination begins as the initial year’s ratio of debt (GovDebtAbs) to relative price adjusted GDP (GDPPOTRPA), but we found that it enhanced long-term model behavior to build the ultimate target (GovDebtTargetPercent) on a moving average of that ratio over time (GovDebtTarMov), only allowing the moving average to be changed over time when the debt to GDP ratio falls (thus reducing the target). Further, the ultimate target converges over 100 years from the moving average target to the minimum of the value from the function and the larger of the debt level of the base year and the value of zero. Not shown here are two special rules during the first few years of the model run when the GDP growth rate is specified using data values that can vary dramatically from year to year for a very small number of countries.
The debt target value is used within the PID structure with the ADJSTR function to compute sequentially multipliers for government revenues (MulRev) and expenditures (MulExp). That requires the computation for the function of the two difference terms (Diff1 and Diff2), representing the absolute value of the distance from the target and the year-to-year change in that distance.
The PID function also requires the specification of the scaling term, in this case the relative price adjusted potential GDP (GDPPOTRPA) The potential relative price adjusted GDP is used in both the difference calculation and as the scaling factor rather than the actual GDP in order to protect systemic stability over time (use of GDP in the target term can set up oscillations in some feedback loops also involving GDP).
Finally, the function requires scaling parameters for the two difference terms. The implications of these difference terms are different for revenues and expenditures and this discussion beings with revenues for which the scaling parameters are elgrevdebt1 and elgrevdebt2.
The Mul term that the function produces is accumulated over time in the MulRev variable and used within the SAM structure’s elaboration of the various revenue streams that make up total government revenues (GOVREV)―see the documentation of government finance within the SAM structure in Section 3.5.
In completely parallel fashion, adjustment is made to the expenditure multiplier (MulExp). Tuning of the model reinforced the need for the elasticities on the expenditure side (elgexdebt1 and elgexpdebt2) normally to be lower than those on the revenue side (governments are more likely to adjust revenues than expenditures). However, when revenues and expenditures get substantially out of balance, there are times that some "extra kick" on the expenditure adjustment is needed on the year-to-year difference term parameter and that is provided by the elasticity multiplier (ElMul) based on the imbalance indicated by the ratio of revenues and expenditures (but not to exceed a factor of 5). Further, it was found that the behavior of expenditures is more subject to potential oscillation than that of revenues, in part because of the push that they receive from demands for them from various other models in the IFs system, especially with scenario interventions representing policy pushes. Therefore, the coefficient on the difference term (Diff2), set exogenously as usual with the PID function to be about a factor of 2 larger than the coefficient on the absolute error term, benefits from a further doubling within the code to dampen such oscillation.
Finally, exogenously specified changes in the level of an economy’s informal or shadow sector size via a parameter (gdpshadowshrm) has implications for government revenues because reduction of the informal share of the economy can enhance tax collection via a tax adjustment factor from informality change (TaxInfAdjustmentFac) as explained in the documentation of informality (Section 7). On the revenue side, the SAM structure in IFs represents such enhancement by direct increase (or decrease) in various tax rates (see Section 3.5.1.2). On the expenditure side, the adjustment factor due to informality change is used to increase MulExp, and because of the cumulation of the impact over time in MulExp, only a tenth of that factor’s size is passed to MulExp in any given year.
If gdpshadowshrm < > 1 then
Within the SAM structure elaboration (Section 3.5.2), the multiplier on expenditures is used to adjust government consumption (GOVCON) and transfers (GOVHHTRN).
4.4.4 International Interaction and Trade Dynamics
The rates and levels of exports and imports (see Section 3.6 for the discussion of use of sectoral exports and imports (XS and MS) in social accounting). This section explains how those variables are shaped by a combination of the domestic price (PRI) and exchange rate indices (EXRATE) using the PID formulation (the ADJSTR function).
Beginning with prices and leaving aside for the moment issues of trade among countries that seems to contradict comparative advantage or that appears to involve both imports and exports of fundamentally equivalent goods and services, at least in the long term, changes in imports and exports respond to domestic prices (PRI) relative to those elsewhere. As a measure of prices elsewhere, IFs uses a world average price (WP), weighting domestic prices around the world by regional gross production (ZS) and adjusting them by exchange rates (EXRATE). The computation of world prices uses lagged domestic prices, because at this point in the flow of the code the recursive equation system has not yet computed current prices.
Exports are responsive in sequential formulations below to changes in production and then changes in prices via respective elasticities. On the production side we begin in each year by computing an export base (XBase). It multiplies an export propensity variable (XKAv) times the sum of two terms. The first term is potential gross sectoral production (ZSP) and the second is the difference between that potential in the current and previous year, multiplied by an elasticity for exports with production potential change (elasxinc). An export shift parameter (xshift) can be used to represent scenarios about export promotion or constraint.
Given the export base, which can be interpreted as a capacity for export were prices not an issue, the export capacity (XC) takes prices into account via a multiplier produced by the ADJSTR function. That function looks via first difference term (Diff1) at the difference between local (PRI) and global prices (WP), using a country- and sector-specific elasticity of trade with prices (elastrpr) and therefore with that price differential. The prices of exports faced by other countries involves the domestic price modified by the exchange rate and any export tariff (XTariffTaxR) imposed. That is compared with the world price modified by such export tariffs in the first model year given that base year values for exports from data reflect tariffs and it is therefore only forecast years, when tariffs on the domestic side are changing that should enter into calculation of price response. The second order difference term (Diff2) represents how differences between domestic and world prices (Diff1) change over time; it compares the differences in a current year with a moving average of those differences across time, thereby reducing volatility in the multiplier. The impacts of first and second order difference terms are controlled by parameters (elprx1adj and elprx2adj).
Import capacities or demands (MD) are analogous. Whereas exports are tied to production, however, imports are tied to a demand base (DBase) made up of final domestic demands plus gross sectoral production potential (ZSP). The use of both element types helps in representation of countries and sectors that may be either predominantly consumers or predominantly producers. When GDP growth rate is exogenously specified via a value for gdprext, the actual level of ZS substitutes for ZSP; the reason is that in early model years gdprext, reflecting historical data from the IMF, can vary greatly year-to-year for some countries and imports should respond to such variation.
The import base (MBase) from which the import demand (MD) is calculated could be tied directly to DBase, but is tied instead to a smoothed version of it (SmoothDBase), which is set to DBase in year 1. That smoothed base is computed as a moving average across time, with the mbasehw parameter specifying how much to tie to the historical term increased by a smoothed value of GDP growth rate (SmoothGDPR) and what portion to tie to DBase.
Given the smoothed demand base for imports, the basic value of imports (MBase) uses that and the propensity for imports as a portion of the base caried over from the last year (MKAv). The MKAv term is a moving average of imports as a portion of demand that will be updated after the completion of global trade balancing.
And given the basic imports it is possible to compute the import demand (MD) as the product of that and a multiplier (Mul) from the ADJSTR function. Although it is very unlikely to happen often, that calculation is constrained by the smoothed demand base times 130% of the propensity for consumption in the model’s base year (MKav at t=1). The logic of values entering the adjuster function is the same as explained above for exports. There is a comparison in Diff1 of the prices of sectoral imports from those countries providing them (domestic prices times the exchange rate and inflated by the importing country’s tariff rate) with the world prices (WP). The world prices can be inflated in scenarios with the parameter protectm to build scenarios including simulating import substitution policies that constrain those imports. The differences in the two price terms is translated into the Diff1 term with the trade price elasticity parameter (elastrpr). The Diff2 term is the difference between Diff1 and an import price lagged term (MPrcLag), again multiplied by the elasticity. As with exports, the lag term is a moving average.
World export capacity (WXC) and world import demand (WMD) are simply sums across regions.
These will always be somewhat different. Actual world trade (WT) is set at the average of the two.
We can then update the moving average export (XKAV) and import (MKAV) propensities for the next cycle. This requires historical weight parameters (xhw and mhw) for exports and imports.
The resultant values for XS and MS are used in social accounting as described in Section 3.6.
4.5 Analyzing Behavioral Dynamics
Given the earlier elaboration in integrated economic model documentation of economic production and of the SAM, and the discussion in this Section 4 of model equilibration dynamics, many of which use the PID, the foundations are in place for helping model developers and users explore and understand model behavior in the Base Case and other scenarios. Clearly, the stock and flow variables plus the equilibration-driving variables are important ones for understanding overall model behavior.
The model is equilibrium-seeking, perhaps more accurately identified as equilibrium-chasing given the constantly changing patterns of underlying variables that can push it away from the multiple equilibria it seeks. That is, no aspect of the system will be in exact equilibrium at almost any time point and disequilibrium can be considerable. The extent and character of disequilibrium provides much information:
- Identifying countries that may merit additional attention with respect to the data load. When initial conditions in the base year suggest very significant disequilibria, attention to data values and base year estimations is often warranted. Despite the analytical capacity of the data preprocessor, some initial conditions for the base year, especially when they are estimated based on data of multiple recent years, but even when they are seemingly solid variable values such as the size of the GDP, will be proven inaccurate in future data releases or revised calculations.
- Suggesting unique and often extreme base year and early forecast period conditions that countries face and will need to address. In quite a few cases, especially for lower income and/or rapidly developing countries, disequilibria point to patterns within economies that are unsustainable and provide warnings of challenges or trouble to come. Examples can include considerably more rapid growth in government expenditures than in revenues and very great current account imbalances.
- Pointing to strengths and weaknesses of model formulations. Turning to longer-term analysis in particular, a failure of stock variables to stay within reasonable ranges around a target level can suggest the need for reconsideration of flow adjustment specifications. At one point in IFs development, international debt levels relative to GDP were constantly and substantially increasing for many countries across the century, a pattern impossible in the real world. Changes in the feedbacks to elements of the current account, especially trade balances, addressed that issue.
Every version of the model and all scenarios will produce at least marginally different forecasts or projections and suggest different versions of the issues above. A model like IFs requires constant revision in the face of new information. The patterns and analysis here are from the Base Case of Version 7.93.
We begin looking at those forecasts through use of the identity that is regularly considered in economic forecasting, namely S – I = X – M. The behavior of IFs relative to that identity helps survey the system’s integrated behavior across households, firms, and governments, as well as their interaction across all the countries in IFs. We then drill down into the various stock and flow variables more specific to the multiple underlying equilibration dynamics in IFs across specific elements of the SAM.
4.5.1 Savings and investment
The introduction of Section 4 indicated that the IFs approach significantly elaborates that simple S – I = X - M equation often used to represent equilibration of flows in economic models. The elaboration noted that the equation itself can more accurately and fully be spelled out as: national (or domestic) public and private savings minus investment (the sum of gross capital formation and change in inventory stocks) is equal to the current account. Thus:
Domestic Savings – Investment = Current Account
In model descriptions the current account is often identified as equivalent to the balance of trade, but it also includes net income transfers from abroad and net current transfers (such as remittance and foreign aid flows). And the introduction pointed out the elaboration within IFs of SAM-based flows, the augmentation of the flow representation with that of stocks, and the use of a dynamic logic that helps shape flow adjustments to prevent unsustainable debt (or asset) levels for key stocks such as sectoral inventories, government debt/assets, and national debt/asset levels.
The elaboration in IFs builds further on extension of the identity to recognize that the current account balance is equal with opposite sign to the capital account (also recognized as foreign savings). Financing a current account deficit (a negative current account) requires net positive inflow of capital from abroad, a net inflow of foreign savings. That is, the current account and capital account or foreign savings inflow have opposite signs.
-Current Account = Capital Account = Foreign Savings Inflow
Hence the identity can also be written as
Domestic Savings – Investment = - Foreign Savings Inflow
and therefore
Domestic Savings plus Foreign Savings Inflow = Investment
or
Total Savings = Investment
In IFs the variable SAVINGS is the sum of domestic and foreign savings. The domestic portion of SAVINGS is the sum of household savings across household types (HHSAV), firm savings (FIRMSAV) and the balance of government revenues and expenditures (GOVBAL), while the foreign portion is named FORSAV. Foreign savings is the negative of current account (CURACT), which is the sum of the trade balance (X-M) plus net receipts of foreign aid (FORAID) and remittances from abroad (XWORKREMIT). I is investment and is the sum of gross capital formation (IGCF) plus the change in inventory stocks (ST). Thus, in terms of IFs variables, important elaborating equations are:
SAVINGS = HHSAV + FIRMSAV + GOVBAL + FORSAV
FORSAV = - CURACT
I = IGCF + Delta ST
The above flow variables involve multiple equations and equilibration processes that earlier documentation sections have explained, and some of them will be focal points in subsequent discussion. When examined at the aggregate level across the entire IFs economic model, however, those equations and dynamics should be fundamentally consistent with the Total Savings = Investment identity.
One way of checking that is to examine Total Savings – Investment as a percentage of GDP, which should be equal to or very close to zero across countries and time. Figure 4.1 shows that this is very close to true in IFs at the global level, with some slight differences related to the complexity of initial data representations, model formulations, and the temporal dynamics of calculations in the equilibrium-seeking IFs system. The differences between savings and investment remain well below 1 percent of GDP across time.
At a national level, variations from the identity can prove significantly greater. Yet, it is a small subset of countries that exhibit sometimes quite substantial variations and provide information to us about data issues, challenges facing countries, and IFs structure. For instance, even in the 2017 base year country values informed by the best data available to us do not all exhibit a precise identity of total savings and investment.
In Figure 4.2 Gambia has the largest 2017 positive discrepancy at 4.4%, followed by Rwanda and Liberia near 2.5%. The black line with a large peak in 2022 followed by a long negative wave is the Ukraine and reflects the impacts of the war. The rising grey line is Somalia and suggests the complications of modelng a very poor country with long-term dependence on foreign aid and remittances as well as uncertain domestic investment opportunities. Countries with significant deviations from the identity merit further attention with respect to initial condition data and the conceptual/modeling formulations in IFs.
4.5.2 Inventory stocks and associated stock and flow analysis
Turning from an examination of the high-level aggregation represented by the SAVINGS = I identity to the agent categorization and disaggregated dynamic variables of the model, Figure 4.3 shows how inventory stocks (ST) summed across the six economic sectors of IFs rise or fall as a portion of gross domestic production (ZS), some of which serves intersectoral flow needs in the SAM as well as meeting final demand. The relatively smooth change in the stock ratios for most countries suggests considerable balance between flow of supply and demand. Some of the variation in the ratio to gross production across time and countries can be explained by potentially very different economic patterns with respect (1) the extent that demand from household consumption, government consumption, capital investment and exports is met by domestic production, (2) the extent to which demand is met by domestic production plus substantial imports, and (3) the extent to which country-year demand reflects entrepôt economy patterns of import and re-export. Such highly variable economic patterns drive different needs for inventory stocks and equilibrating dynamics across country-years. For instance, the demand for sectoral imports in entrepôt countries tends to be a very high ratio to gross domestic production because of the high level of exports.
The bubbles and therefore periods of disequilibrium in the graphic, especially the downward ones indicating shortage of supply relative to demand, suggest one or more of the three insight sets laid out earlier, namely potential weaknesses of initial data, challenges facing the country (i.e., high external debt levels), and model formulation issues. Important note: Countries cannot logically have deficits in inventory stocks, although they can have extremely low levels and unmet needs. IFs allows the calculation of negative inventory stocks as a way of sending signals back to the flows in the SAM; moreover, across time it pushes stocks back into positive territory (covering interim deficits) so that there is no temporally independent free lunch.
The early blue downward bubble and subsequent wave pattern is São Tomé and Principe. The long downward aqua bubble is the Solomon Islands. The long green upward line is Hong Kong and the long gray upward line is the Democratic Republic of the Congo.
Numerical analysis of such countries helps explain these deviations of countries from the more common pattern and can provide insights to be gleaned from them. Focusing on São Tomé and Principe, the first four columns of Table 4.2 provide information on final demand components and the fifth shows the numerical values of inventory stocks relative to gross production (ZS). Note especially in the first column the very high portion of total production for final demand (PFD) and therefore of GDP that household consumption (CS) constitutes in 2017, taking nearly all of GDP. That high level is mostly “paid for” in the initial final demand picture by a surplus of imports over exports (a net trade imbalance of 38% of GDP). Both of those columns suggest the need for substantial changes in coming years–household consumption tends to average 55-60% of GDP across countries and such large trade imbalances are seldom sustainable absent continous inflows such as remittances and foreign aid. Even those current account terms are not large enough to offset the trade deficit in the base year, causing external debt to blossom quickly for São Tomé and Principe. That sets in motion equilibrations in IFs including reduction of the household consumption share of GDP, as well somewhat less reduction in the near-term government consumption share and a steady reduction in the trade deficit. Such substantial changes are difficult (nearly impossible?) for countries to make, helping explain the oscillation of the country’s savings and investment balance over a long time.
The forecasts for change in gross capital formation and government consumption are contrary to corrective behavior but in line with common development patterns and magnitudes for those values. The adjustments in consumption and net exports stop the growth in foreign debt percentage of GDP before 2030 as the current account balance turns positive. Inventory stock values remain very low and decreasing, and the figure above showed continued deterioration through 2040 and then rebound in a somewhat oscillating pattern. Assuming that the initial data values prove reasonable with review and revisions, all of this suggests that São Tomé and Principe faces some very significant challenges in the coming years.
4.5.3 Price, capacity utilization, interest rates, and exchange rates
The analysis of inventory stock equilibration helped identify some of the countries that might struggle most to address challenges that may put substantial pressure on the efforts to meet final demands for good and services. Four variables that strongly influence flows largely shape the how flows direct the ongoing pursuit of equilibration domestically and internationally thereby generating changes in inventory stocks over time. The first three of these (sectoral prices, capacity utilization, and interest rates) have key domestic roles in the ongoing market-based reconciliation of demand and supply forces, while exchange rates interact with sectoral prices in affecting the trade flows that play a dominant role in maintaining international balances. Reviewing changes within the base case in all four help us take a deeper “look under the hood” at the dynamics of possible adjustments of final demand and inventory stocks.
4.5.3.1 Price index behavior in equilibration
A price index (a value-added weighed average of prices across sectoral base year values of 1) is shown in Figure 4.4. Although the century-long rise in prices for none of them is especially great, countries with highest values over time are São Tomé and Principe (blue bubble) and Timor-Leste (black with steady rise that starts in early years). Discussion above explained issues facing São Tomé and Principe.
The issues facing Timor-Leste are quite different and are related substantially to very unusual patterns of government revenues (highly driven by oil exports) and expenditures (at high levels given social needs and those revenues, but increasingly constrained in recent years with lower energy prices). We shall return to discussion of Timor-Leste when discussing interest rates.
4.5.3.2 Capacity utilization behavior in equilibration
Turning in Figure 4.5 to the second variable that affects inventory stocks, it is not surprising that capacity utilization tends often to be highest in those countries where stocks are low and domestic prices high: São Tomé and Principe (blue bubble in the first half of the century) again stands out, this time in terms of upward pushes in capacity utilization. Falling capacity utilization is also important. DRC is the turquoise line at the bottom. Finally, the very early jumps in Guyana and to a lesser degree Libya result from very high exogenous GDP growth rates in those years and for Libya reflect recovery from earlier poor years. IFs currently represents base year capacity utilization at the same level for all countries. The many spikes downward in 2020-21 represent primarily COVID impacts.
4.5.3.3 Interest rate behavior in equilibration
A third variable that plays a role in equilibration of inventory stocks is interest rate. The two bubbles in Figure 4.6 around 2025 are Timor-Leste and Guyana. The blue line double bubble is São Tomé and Principe. The two countries with highest values late in the century and in 2100 are Timor-Leste and Tajikistan. The grey line lowest value in 2040 is Puerto Rico and it falls to zero in about 2060 with long persistence there. Puerto Rico has a complicated commonwealth status relative to the U.S., just as Palestine, Hong Kong and Taiwan with their complicated geopolitical statuses are often not identified as countries. Data for all four entities are thus difficult to obtain in standard international sources, perhaps most especially for Puerto Rico. In addition to it, however, many countries fall toward/to zero including UK and United States. Given that interest rates in IFs react to inventory stock rise and fall and that IFs does not have a monetary sector, rate changes and even levels across time can be interpreted generally in real rather than nominal terms (although initial data represent data and are nominal); real interest rates across countries and time are often zero or even negative.
Timor-Leste merits some additional attention because it exhibits outlying behavior here and on other variables. Table 4.3 shows that it has some very unusual initial conditions in 2017, including a high level of net international assets coupled with large trade and current account deficits. It also has a high level of government consumption as a share of GDP coupled with a low level of household consumption. A major reason for these unusual patterns is the creation by the country in 2005 of the Timor-Leste Petroleum Fund, fundamentally a sovereign wealth fund, to hold much of the earning from very substantial energy exports in subsequent years.[2] The IFs system does not have a sovereign wealth fund variable and therefore does not protect those combined net positive international asset and current account deficit positions from rapidly pushing down exchange rates to “correct” the high level of imports that support the current account imbalance, thereby rapidly running down inventory stocks. That pushes up interest rates (and the interest rates and low inventory stocks push down household consumption and capital formation). Similarly, the absence of representation for governmental transfers into a sovereign wealth fund underlies the high government consumption (expenditures cannot in IFs be sent instead to such a fund) The combination of somewhat uncertain initial data conditions (including a large outward flow of remittances that seems improbable) and the absence of formulations in IFs around sovereign wealth funds create some rough behavior for the country’s forecasts, especially in early years.
4.5.3.4 Exchange rate behavior in equilibration
Exchange rates is the fourth of the price/rate variables that help shape flows in the pursuit of stock equilibria. The significant bubble in Figure 4.7 is Yemen, although it is important to note that the absolute change in the index (Base 1) is not that huge. Still, why does Yemen exhibit that pattern? The table below the graphic helps explain. Yemen is unusual in that it is one of the poorest countries in the world, but one for which financial inflows from abroad, in the combined form of foreign aid and worker remittances, constitute about 30 percent of GDP, roughly equivalent to the deficit in the trade account. The equilibration processes in IFs improve the trade balance over time and the share of GDP directed at household consumption declines toward global patterns. These forces, along with the long-term persistence of aid and remittance inflows (albeit gradually declining as shares of GDP) in the Base Case push the international debt level downward quite sharply after mid-century, much as they appear to have helped doing between 1990 and the IFs base year. The growing foreign asset surplus drives the exchange rate upward.
All of this said, the base case forecast for Yemen in Table 4.4 across these variables looks highly improbable on many of the fronts discussed here, including the continued inflow of financial support, the reshaping of consumption behavior, and the movement toward more balanced trade. The initial conditions setting in motion the dynamics in IFs are strongly shaped by the extreme conditions of the contemporary war, while the dynamics represented in the model are heavily shaped by patterns experienced in countries that have not suffered such ongoing intense conflict. The best that can be said is that (1) the graphic bubble draws attention to the great challenges (with some opportunities) that Yemen faces and that (2) Yemini forecasts are subject to great uncertainties concerning how the country’s future might unfold. In collaboration with the United Nations Development Programme the Pardee Center has done several studies focused on possible alternative futures of Yemen (Bohl et al 2018; Moyer et al. 2019a and 2019b). More generally, the Center has done country level analysis on other often challenging countries including Brazil, Egypt, Guinea Bissau, Mexico, Nigeria, Moldova, North Macedonia, Peru, South Africa, Uganda, the Ukraine, the United States, Yemen, and Zambia, as well as various more regionally focused work (see the Pardee web site at https://korbel.du.edu/pardee).
4.5.4 Government debt/asset levels and flows
Moving from looking at the entire economy (building on the S – I = X – M identity) and from exploing some of the key variables shaping equilibration proceeses, we turn to focusing on two actor categories beginning with government. Equilibration of government revenues and expenditures is important in IFs in substantial part because of its linkage to much scenario analysis including policy interventions directed at pursuit of the Sustainable Development Goals. The key stock variable is the level of govenrment debt as a percentange of GDP, as shown in Figure 4.8.
Very many countries show early movement into greater governmental debt or net asset conditions, because data indicate substantial imbalances between expenditures and revenues in the base year. The model moves those countries toward equilibrium over time (Section 4.5.4 detailed the feedbacks in the model from debt levels to adjustments in both revenues and expenditures). The high grey debt bubble in the figure above is Lebanon, the green one is Libya, and the black one is Venezuela, none of which are surprising given current conditions in those countries. The country with the highest initial value is Japan (brown), suggesting that high debt values are not necessarily such a problem for a highly developed country with strong export capacity and governance. Two countries with the largest negative debt (and therefore asset positions) in the late 2020s are Hong Kong and Syria. The surplus government balance for the latter is driven by foreign aid receipts at approximately 50% of GDP, which slowly decline over time but which the model indicates could still be 30% in 2100. That pattern raises significant questions, given the improbability of sustained (and quite probably even near-term) foreign assistance inflows at such high levels. It also raises questions about the model’s direction of such large flows into government revenues, as it routinely does for countries pursuing economic development, given that the war in Syria has generated need for and attention to assisting, often directly, various subpopulations and refugee groups.
Figure 4.9 shows the flows that underly the dynamics of governmental financial stocks over time in the figure above. The downward bubbles in the early years reflect the net deficits in revenue within Venezuela, Libya, and Timor-Leste. The deficits lead to mid-century surplus revenue to reduce the resultant debt load. That pattern obviously assumes ultimate repayment of the debt rather than default, which the model cannot reasonably forecast but might well occur and can be introduced via scenario intervention (using the govdebtchg parameter). Again, it is important to understand that Base Case forecasts for countries that are outliers most often suggest patterns that are highly uncertain and even improbable, given the magnitude of the challenges that the outliers face.
In terms of net revenue surplus during early years, again we see Syria and Yemen, as well as Somalia at 8 percent or more surplus. For each of these countries much of the foreign aid responsible for those apparent (and questionable) surpluses is not actually going to governments, but directly to people (and for some countries perhaps via corruption to individuals rather than the larger population). Norway and Singapore at closer to 5% do run domestic-revenue based surpluses to expenditures (with Norway directing some money to a sovereign wealth fund).
4.5.5 International accounting
Earlier discussion of changes in inventory stocks over time discussed the pressures faced by a considerable number of countries to reduce the challenges to supply-demand balance posed by trade deficit positions via adjustments in some combination of domestic demand or trade deficit itself. An even more direct pressure for adjustment in trade balances often comes from external debt levels relative to GDP, which Figure 4.10 shows.
While most countries exhibit patterns of net debt or assets (negative debt values) over time within 100 percent of GDP, several countries have more irregular patterns with bubbles of net debt or assets. Among the most significant is the rise and then fall into significant net asset position of the Sudan (blue line), the high bubble in the 2050s of Syria (black line), and the rise and fall of Afghanistan (large dark green circles). The pink bubble of debt in early years is Burundi. In sharp contrast, the long run (red line) of net high asset levels with a bit of decrease is Luxembourg and the similarly long run (green line) is Hong Kong. Libya (darker green line) and Puerto Rico (grey line) show surprisingly high levels of net international assets in the base year. In the case of Libya the value of 206% of GDP comes from the IMF’s net foreign asset data series. For Puerto Rico[3] there are no direct data to initialize this variable and the preprocessor integrates a long data series on its trade surpluses that can provide an estimate of accumulated net asset balance (that is bound at 200% of GDP). All four countries with very high net asset values in the base year remain in net asset position through the century because model formulations use initial asset values as slowly eroding targets in the dynamics of exchange rates.
In general, various factors drive values for some of the more problematic countries: (1) potentially questionable initial conditions (as for Libya and Puerto Rico) (2) more understandable long wave-behavior for countries (e.g., Afghanistan, Burundi, and Syria), and (3) questionable model dynamics (the Sudan).
In earlier versions of IFs (prior to 7.92), international debt and asset values were allowed to grow as percentages of GDP to very high values, largely without constraint. Such patterns inappropriately overlooked the supply-demand balancing of external positions that is a fundamental element of overall economic model equilibration. In recent versions of IFs very large imbalances are not allowed, and over time the model seeks to maintain relative stability in values of net external debt and asset holdings. The target is “relative stability” because there is not a clear target globally for national holdings of gold, currency, and other assets or of debts pegged to them. Section 4.4.4 explained the interaction of debt/asset stocks with the adjustment of trade flows.
4.5.6 Long-term final demand patterns
Behavioral dynamics in IFs in the Base Case and all other scenarios are strongly shaped by the equilibration processes that this section has laid out and explored. They are also, shaped by much else including the basic final demand shares of GDP represented by household consumption, gross capital formation, and government consumption as the century unfolds and countries develop. Although those patterns can vary quite significantly across countries and time, Figure 4.11 suggests the very considerably stability of them globally across time. That picture does conceal, however, the forecast that low-income countries will experience about a 10 percentage-point decline in household consumption share of GDP across the century, most of which occurs by mid-century and is offset by a similar movement of trade in those countries from substantial deficit toward a balance of exports and imports. Figure 4.12 shows the very considerable country-specific and temporal variation of household consumption shares of GDP, with some narrowing of that variation across the century, in association with the movement of low-income countries toward more balanced trade positions. In that graphic, initial values for consumption share of GDP for Somalia (grey line) and Eritrea (purple line) above 100% reflect aid and remittances to Somalia and remittances to Eritrea, but also they suggest unsustainability of those patterns in the longer term.
5 Bilateral Elaboration of Trade and Other Interstate Flows[4]
5.1 Introduction
5.1.1 Background and motivation
Many users of the IFs system have interests not just in the country, country grouping/regional, and global values of trade, foreign aid, foreign direct investment (FDI), and other international economic variables that are important in our representation of the social accounting structures of all countries, but in the patterns of those values among countries―that is, in bilateral (also known as dyadic) connections. Those interests can be both in the drivers of alternative patterns of economic connections and in the forward impacts of them. The IFs representation gives attention to both drivers and impacts.
With respect to drivers, much existing analysis of them is relatively short-term and can be undertaken with fairly traditional economic models. For instance, there are many influences of trade policy including tariffs on bilateral trade patterns. CEPII (Centre d'Études Prospectives et d'Informations Internationales/Institute for Research on the International Economy) heavily uses the MIRAGE model (Modeling International Relationships in Applied General Equilibrium) to explore the impacts of tariff barriers and trade protection, especially in the agricultural sector (Decreux and Valin 2007). The Pardee Center has similarly used representation of the drivers of bilateral trade including tariffs in analysis of conditions for success of the African Continental Free Trade Agreement (Kabandula, et al. 2020).
The Pardee Center has also analyzed alternative scenarios of changing trade patterns between Latin America and the broader world. Those scenarios have implications for the region’s differential political relationships with China and the United States (Prazeres, Bohl, and Zhang 2021) and therefore shift attention significantly from the drivers to the impacts of trade patterns. Such analysis also very often directs attention to the longer term, because political relationships tend to change relatively slowly.
Attention to bilateral or dyadic political interactions can sometimes be found in longer-term models of international relations in which attention to dyads is very important; in those models, attention to the obvious two-way relationship of dyadic political and economic linkages is sometimes represented. For instance, the GLOBUS project represented both political and economic relationships bilaterally and linked them, focusing on the impacts that political relationships have on trade (Bremer 1987).
In reality, representation of bilateral economic flows is not common in long-term economic forecasting like that done with IFs or in integrated assessment models, but rather in more purely economic models with shorter-term forecasts. Unlike most shorter-term economic models and also unlike other integrated assessment models (IAMs), however, IFs does include representation of domestic and international political variables, thereby also motivating the representation of dyadic economic connections and their longer-term forward impact as well as their drivers. For instance, the Pardee Center has created a measure of Foreign Bilateral Influence Capacity (FBIC) with economic, political, and security dimensions―the share of a country’s trade that flows to or from another country is an important element of the bandwidth of such influence and allows us to think about its broader political implications in the longer run (Moyer et al., 2018: 8-9).
5.1.2 Basic approach
5.1.2.1 The gravity of the model in trade
The primary model structure used to forecast dyadic variables in IFs (and most other economic models) is the gravity model. The gravity model of dyadic trade, as put forward by Tinbergen (1962), posits that bilateral flows are directly related to the economic size of the trade partners and inversely related to the distance between them (Yotov et al. 2016) The gravity model helped address in practice the limitations of the Hecksher-Ohlin theoretical model (with roots to work of Ohlin, 1933), which tied trade flows to relative factor endowment in elaboration of Ricardo’s theory of comparative advantage. A challenge to comparative advantage and Hecksher-Ohlin was the recognition that trade often, as with high-income country exports of labor-intensive goods even to labor-intensive countries, seemed to flow in contradiction to relative factor endowments (the Leontief paradox). Armington (1969) elaborated the gravity model to include the recognition (often described as an assumption) that goods from different sources are imperfect substitutes, therefore facilitating trade of categories of goods that might on the surface appear identical. The gravity model, elaborated with the Armington assumption and using elasticities of substitution to represent implicit patterns of such differentiation of goods, has become the “workhorse” model for forecasting dyadic trade and other bilateral interactions. It is the foundation of the approach within IFs.
The gravity model’s name has its origin in Newton’s law of universal gravitation due to the similarities in form and the inclusion of mass and distance. In its most basic form, the model estimates trade potential (exports, imports, or overall trade) between two countries as a function of the “mass” of the two countries (usually GDP), and reduces the trade potential as a function of the distance between them.[5] Variations of the gravity equation can add complexity, such as accounting for multiple-sectors. Models commonly incorporate some trade frictions and promotors representing the economic, geographic, and political environment of and between countries. For instance, de Beneditictis and Taglioni (2011) explored the implications of trade policy within the European Union. The Head and Mayer (2014) survey of theory, models, and methods includes a table of common variables and their average coefficients from over 2500 different models (see Table 5.1). Piermartini and Teh (2005) usefully provide a basic historical and design overview of gravity models in the context also of computable general equilibrium models and the use of social accounting matrices, all of which are important in the IFs system.
Gravity-based analyses are especially frequently employed to evaluate the impact of changing trade policy such as joining or leaving a regional trade agreement, or to better understand the importance of variables in determining trade. In applying the model to long-term projections, we aim to include variables that are most relevant and explain the largest portion of trade flows, as well as those that provide policy makers with levers to simulate meaningful interventions across the economic six sectors represented in IFs. The choice and statistical specification of these variables are explained in greater detail in Section 5.3.
Trade projections in IFs use a hybrid approach, combining country-level exports and imports estimated by a dynamic-recursive computable general equilibrium (CGE) model with bilateral distributions informed by historical patterns and a gravity model. The default bilateral trade representation in IFs computes dyadic trade (which is inherently directed) as a satellite or constrained structure within the monadic or country total representation of trade (the monadic equations are documented in the discussion of the social accounting matrix structure in Section 3.6.1).
At the country-level we project export capacities and import demand across five goods sectors (agriculture, energy, materials, manufactures, ICT) and services. For the model’s base year, exports and imports are then distributed bilaterally according to historical patterns captured in the UN Comtrade data. This distribution evolves over time according to a sector-specific gravity equation, which is responsive to tariffs and trade complementarity, among other promoters and obstacles to trade.
Since the trade model is embedded within the broader IFs system, monadic and monadic-constrained dyadic projections are informed by a wide range of variables related more broadly to national economies,[6] such as resource constraints in physical sectors (agricultural and energy), and sector-specific demand for goods and services, which are responsive to demographic dynamics, savings/consumption patterns, and the broader dynamics of national economic structure and current/capital accounts. Optionally, the dyadic representation can drive the monadic one, but that approach is not always recommended in trade modeling, and it is not fully developed in IFs,[7] and is understood to be generally inappropriate for use in longer-term forecasting. The use of a monadic trade representation to frame and constrain dyadic flows avoids the concerns raised by Anderson (2010) regarding the gravity model’s limited ability to project returns to scale and market structure, and instead reflects his observation that “gravity is about the distribution of given amounts of goods in each origin drawn by given amounts of expenditure in each destination” (p. 39).
5.1.2.2 Looking beyond trade
The gravity model has been used most extensively in the analysis of bilateral trade patterns; however, it has also been applied to other international flows such as FDI and migration (Lewer and Van den Berg 2008).
IFs currently forecasts three types of bilateral flows using a gravity approach (see Table 5.2). These include trade (imports and exports by sector), foreign direct investment (inflows and outflows), arms trade, and migration (inflows and outflows). It is planned that foreign aid will in the future be represented in gross rather than net flow terms and can then also be elaborated dyadically; bilateral flows are currently represented with only a placeholder formulation. The model includes other dyadic variables, including embassy establishment and membership in treaties, alliances, and intergovernmental organizations that are forecast with other formulations or held constant over time and used primarily in scenario analysis. We also project a series of composite indicators built from these bilateral variables. Most of these relate to the projection of intrastate influence (including dependence, bandwidth, and their subcomponents), and are the simple linear combinations of various bilateral and country-level indicators.
Bilateral forecast variables in IFs can be broken down along two dimensions. First, those like shared IGO membership that are undirected flows (actor-to-partner and partner-to-actor share a value) or directed flows such as trade exports and imports (actor-to-partner and partner-to-actor have different values). Second, variables can either be constrained by a core IFs monadic variable or unconstrained and potentially overriding or determining the monadic calculation in IFs.
| Constrained | Unconstrained | |
| Directed | Trade (default approach)
Foreign aid (under development) Foreign direct investment (FDI) Migration |
Trade (alternative approach)
Arms trade Level of representation (embassies) |
| Undirected/Shared | Shared IGO memberships
Shared alliance memberships Shared treaty ratification or signing |
Table 5.2 Alternative modes of dyadic representation for variables in IFs.
Source: David Bohl.
Our initialization and model computation processes vary based on whether the variables are unconstrained or constrained, directed or undirected. Data values for initial conditions for constrained variables go through a transformation to enforce consistency with monadic estimates. Data values for initial conditions of variables in other cells of Table 5.2 are simply pulled from the relevant historical series.
Constrained directed variables are summed by partners for each actor to calculate the actors’ aggregate values. These aggregate values are then used to calculate a share of the monadic variable’s value (both in computing initial year dyadic values and in year-to-year computations of the model) that we attribute to each country in the pair. This share is then multiplied by the monadic variable to give us our final dyadic values. Put formally:
Ultimately, all bilateral variables will be constrained. The second dimension at that point might be flow or stock variables, with the gravity-based variables (trade, aid, FDI, migration) being flow-based, and the other political variables being estimated/distributed with some different form. That will mean that IFs will only have the directed/undirected dimension. Sometime later we may introduce bilateral drivers of monadic forecasts.
5.2 Data Foundations
The Diplometrics project of the Pardee Center focuses heavily on international political variables (see again Table 5.2) and the bilateral data gathering and processing aspects of that project have proceeded in parallel and in interaction with bilateral economic variable elaboration. The system to store, import, and access bilateral trade data is generalizable to all dyadic data with little effort. Due to concerns over the size of the files and the runtime of the model when forecasting bilateral interactions, at present we include neither the dyadic historical series nor the files needed for bilateral forecasts in the packaged version of IFs.
5.2.1 Activating bilateral data, formulations, and display
Forecasting bilateral flows is computationally intensive and the IFs project has been developing the formulations for them gradually over time. For both reasons, the default mode of IFs represents trade, foreign aid, and FDI only monadically. Turning on the dyadic representations requires three steps. The first is downloading all the initial condition files for bilateral flows to make them available to the data preprocessor. These are at https://ifs02.du.edu/BilateralInteractionData/. Upon downloading the requisite files, the user must then unzip the package and place them inside the DATA folder of their IFs install model version (this is not something done in the web-based version of IFs). The second step is rebuilding the IFs Base Case with selection when doing so of the “Using Bilateral Data” option on the page that appears when rebuilding the base. The third is then (after completing the base rebuild) to set the parameter bilateralsw from the default 0 value to 1 and rerun the model. This turns on all bilateral logic except for migration. Migration is activated with migratesw. We have broken them up because they can take quite some time to run and running just one or the other (as needed for projects) can cut that time down significantly. These steps will also populate a specialized display for projections of dyadic variables (discussed in Appendix A).
5.2.2 Data sources and preparation for data forecasting
Appendix A (Section 12.13) also identifies the specific files that are activated for use in IF when the bilateral switch is on, and it shows file structures. It also describes the preparation of those files from raw data sources both for estimation of the gravity model and in the IFs system’s forecasting. For example, it explains the aggregation of commodity-level trade data to IFs sectors. The primary data sources are CEPII’s BACI (Base pour l’Analyse du Commerce International) database[8] and the United Nation’s Comtrade (COMmodity Trade by name, but including services, which the significantly derivative BACI data do not). Thus, for trade in goods we use the BACI database, which is built from and improves upon UN Comtrade data by reconciling declarations recorded by exporting and importing partners.[9] For bilateral service data, we use the UN Comtrade data directly. Some data preparation is done outside of the IFs system, but when the IFs Base Case is rebuilt the IFs preprocessor fills holes and reconciles monadic trade totals and bilateral flows. When the initialization processes are complete in the preprocessor, the IFs model dyadic variables have initial values.
5.3 Estimating gravity equations for trade
Given sectoral nuances, we have created separate bilateral models for each of the six primary sectors of trade—agriculture, energy, materials, manufacturing, services, and information and communication technology. With the two-fold aim of explaining the largest portion of trade flows and providing policy makers with levers to simulate meaningful interventions, these models include variables relating to overall supply and demand (value added and/or GDP), distance between countries, the sector-specific complementarity of trade between countries, and the trade-weighted tariffs imposed by a country on the sector-specific imports from another.
After preparing a panel dataset for the above variables, we estimated the following gravity equation for each sector, outside of the IFs model:
Here, i and j denote exporters and importers, respectively, t the year, 𝜋 time-invariant exporter fixed effects, 𝜒 time-invariant importer fixed effects, 𝜇 year fixed effects, X1 through Xk a suite of time-varying monadic and dyadic factors, 𝛽1 through 𝛽k their respective relationships with trade, and 𝜀 the idiosyncratic error.
This gravity-based model (Yotov, Piermartini, Monteiro, & Larch, 2016: 62) — built upon Anderson’s (1979) theoretical foundations emphasizing the attractive forces of nations’ metaphorical mass and their literal and metaphorical distance from one another — uses Poisson pseudo-maximum likelihood estimation, which multiplicatively assesses the drivers of trade, effectively controlling for the heteroscedasticity and inflated zeros common in trade data (Santos Silva & Tenreyro, 2006, 2011).
The variables underlying the estimates, as shown in Table 5.3, are:
- Value added of exporter countries (a mass term for the gravity function).
- GDP of exporter and importer countries (an alternative or supplemenary mass term for the gravity function). Other sections of the economic model documentation explain the database for value added and GDP.
- Physical distance of exporter and importer countries. distance (Distance) is initialized from CEPII’s GeoDist (SeriesDistanceCEPII in the Dyadic Historical Series).
- Tariff data that come from the World Bank’s World Integrated Trade Solution (WITS), which provides bilateral tariff revenue by country-pair at the commodity level.
- A Trade Complementarity Index (TCI) specific to the country dyad and sector. The Trade Complementarity Index, measuring the degree of alignment between one country’s exports and another country’s imports, is calculated for IFs goods sectors data (yet to implement for services) from BACI using the World Bank methodology. The TCI between countries k and j is defined as:
- TCI_ij = 100(1 – sum(|m_ik – x_ij| / 2))
- where x_ij is the share of good i in global exports of country j and m_ik is the share of good i in all imports of country k. The index is zero when no goods are exported by one country or imported by the other and 100 when the export and import shares exactly match.
- Energy production of exporter countries (a mass term for the gravity function, energy sector ony)
Table 5.3 lists the coefficients for each sectoral model.
5.4 Forecasting Bilateral Trade Flows in IFs
Having data consistent with the country and sector representations in IFs, having estimated gravity functions, and having reconciled monadic and dyadic trade in the preprocessor (including filling holes), next steps involve:
- Using the first year of the model’s forecasting scenario runs to compute a function-based value for country-sector-dyad specific exports that can be compared with the data-based value. The difference between them is the fixed effect for each sector-dyad value, that is, the value of dyad and sector specific exports that is unexplained by the parameters and functional form of the gravity model. It is critical to deal in some way with that fixed effect by carrying information about it forward in time.
- Computing values across time, including constraining total bilateral exports for each country-sector by monadic values and passing forward in time the base-year fixed-effects.
The first subsection below identifies the variable names that model users can see in the Base Case and other scenarios. The second subsection explains the logic of forecasting, including the carrying forward of fixed-effect differences between the results produced by the gravity model in the base model year and the dyadic dataset that the preprocessor produced.
5.4.1 Key variables
When the broader initialization processes are complete in the preprocessor, the IFs model variables around dyadic trade have initial values. This subsection identifies the variable names that model users can see in the Base Case and other scenarios (accessed through the specialized dyadic display, Bilateral Interaction Display with Gravity Option, discussed in Appendix A: Section 12.13.3).
There are three primary sets of bilateral trade related variables. The first set (MDYAD… and XDYAD…) pertains to trade flows (imports and exports) by sector (agriculture, energy, ICT, manufactures, materials, and services and indicated by placeholder…) including an aggregate category (total imports and total exports). The second set (DYADTRADECOMPLEMENT… and DYADTARIRATE…) pertains to the dyadic drivers of trade that are used in the gravity model. These variables, initialized directly from data in the IFs preprocessor, are held constant over time; however, each have associated multiplier parameters allowing users to influence patterns of trade. The third set, involving only DYADTARIFFREV…, represents a computed tariff revenue variable.
| Bilateral Variable | Definition |
| MDYAD | Total Imports from Actor to Partner |
| MDYAD… | Sector Imports from Actor to Partner |
| XDYAD | Total Exports from Actor to Partner |
| XDYAD… | Sector Exports from Actor to Partner |
| DYADTRADECOMPLEMENT… | Trade Complementarity Index on Sectoral Exports from Actor to Partner |
| DYADTARIFFRATE… | Tariffs on Sectoral Exports from Actor to Partner, Percentage Rate |
| DYADTARIFFREV… | Tariffs on Sectoral Exports from Actor to Partner, Revenue Dollars |
Table 5.4 Bilateral variables in IFs relating to international trade.
Source: David Bohl.
Note: Variables names followed by an ellipsis stand in for six sector-specific versions. In the model these are articulated as AGR (agriculture), ENE (energy), ICT (information communication technologies), MAN (manufactures), MAT (materials), and SER (services).
The sections below describe the core dynamics that govern dyadic trade projections.
5.4.1.1 First year set up of forecast values: Fixed effects
In much of IFs we compute in the first model year the difference between data values for variables and estimates from model formulations as either an absolute or ratio difference and carry that difference into calculations in subsequent years as a “shift factor.” Often absolute value additive shift factors converge toward 0.0 over a fairly long period and multiplicative shift factors converge toward 1.0. Such convergence represents the erosion of case-specific fixed effects represented by the shift factors with the assumption that they are either simply data noise (perhaps even measurement errors) or the result of additional variables that are unlikely to persist in creating the same pattern of difference relative to the model formulation over time.
For bilateral trade the gravity model does not provide a strong basic for long-term targets of sector-dyad values because in part of the sometimes quite dramatic and difficult to explain differences between those estimates and the initial data values. Instead, we have more confidence in the directions and general magnitude of change that the formulations suggest for dyadic values. Thus, the approach is simply to change the computed and saved dyad values (SXDyad…) over time by the percentage change in the formulation-based estimates year to year, as indicated in the next subsection, thereby leaving the general magnitudes of the fixed effects unchanged.
5.4.2 Year-to-year model computations
5.4.2.1 Basic export calculation
As described above, the preliminary (before constraint) calculation of dyad and sector specific exports is simply the calculated value from the previous year multiplied by the ratio of the gravity function’s calculations in the forecast year relative to that of the previous year (with changes in the drivers between the two years).
Before any further adjustments are made to this calculated value each year, it is saved for use in the following year.
After saving the gravity function-linked value for use in the next year, the calculated value can be adjusted in multiple ways, beginning with the scenario option for users to multiply the before-constraint value for any dyad for scenario analysis purposes by a parameter (tradeexportdyadm) that has a default value of 1.0.
5.4.2.2 Balancing between outflows and inflows matrices
In dyadic analysis, the balancing process between outflows and inflows varies based on whether the forecasted variable is directed or undirected (see again Table 5.2). For directed variables such as trade we simply forecast one side of the flow. With trade we forecast exports and then mirror it to create the respective dyad and sector specific imports.
5.4.2.3 Constraining
At this point the sums for each country of sectoral exports across all targets and of sectoral imports from all sources will not equal the monadic calculation of those values in variables XS and MS, respectively. Because by far the most common use of the model imposes monadic totals on dyadic patterns, a constraining process does that. The first step is computing the sums of exports and imports from the dyadic calculations (XSDyadCalc and MSDyadCalc).
These variables can differ substantially from XS and MS, but coordinating dyadic calculations with monadic ones in the model’s base year generally limits that. A simple normalization of dyadic values for each to XS and MS would result in dyadic trade export and import values that are not mirrored within the dyad. To assure that they do, an iterative process is used that alternates between adjustment of the normalized sector and dyad specific values toward each other and additional normalizations until stable and mirrored values for the dyadic flows are reached that sum very closely to XS and MS. The iterative normalization procedure for doing this involves two functions, AdjustXDyadic which manages the iterations and AdjustXSecDyadicFix which does each iteration. Once the dyadic values sum properly to XS and MS, they will also sum across sectors to monadic values of total exports and imports (X and M).
in interaction with
So that XS and MS remain unchanged and
The other approach is setting a maximum possible value defined by a monadic IFs variable. This approach is used with undirected variables. Variables using this approach include our shared weighted IGO forecasts and our influence forecasts. This approach is implemented by taking the minimum value of the two countries in the dyads’ monadic values and utilizing it as a cap. Put formally:
In contrast, unconstrained variables have no adjustments after they are calculated. After being constrained – if needed –forecasted variables are done being calculated and are saved for usage in the displays as described above. This is currently done with arms trade.
5.4.2.4 Parameters and scenario analysis
Key parameters for use in scenario analysis and model control around dyadic trade are:
| Bilateral Parameter | Description |
| bilateralsw | Bilateral Switch (off by default) |
| bilateraltradeforwardlinksw | Bilateral trade forward linkage switch |
| tradeexportdyadm | Multiplier on Bilateral Trade |
| dyadtariffratem | Multiplier on Bilateral Trade Tariff Rate |
| dyadtradecomplementm | Multiplier on Sectoral Trade Complementary Index |
| xcadjsw | Export capacity adjustment switch |
Table 5.5 Bilateral parameters in IFs relating to international trade.
Source: David Bohl
A number of these have already been discussed:
bilateralsw is necessarily turned on for any dyadic analysis to be done; default value in install versions of IFs and on the web is 0.0 (changing it on the web has no meaning because the web version does not handle bilateral variables).
bilateraltradeforwardlinnksw can be used to influence the linkage of dyadic trade to monadic, overriding monadic values for XS and MS; the default value is 0.0; we make the strong recommendation that it remains turned off and that if turned on that the resultant forecasts be examined only through about mid-century.
tradeexportdyadm can intervene on specific dyad-sector export values as shown in equations above; the default value is 1.0.
Additional parameters are:
dyadtariffratem can intervene on specific dyad-sector tariff rates (used in the gravity calculation every year) which otherwise are fixed across time at base year values; the default value is 1.0
dyadtradecomplementm can intervene on specific dyad-sector trade complementarity levels (used in the gravity calculation every year) which otherwise are fixed across time at base year values; the default value is 1.0
xcadjsw is a switch that can pass through bilateral dyadic trade values to export capacity when import demands increase or decrease; the default value is 0.0. The switch enables economic shocks in one country (namely those resulting in a reduction in import demand) to pass through to their trade partners proportionally to the strength of their dyadic (export) relationship. E.g., if we simulate a Russian recession with this switch set to 1, then export capacity in countries exporting to Russia, will be reduced. We can actually set it to any value between 0 and 1, with fractions passing on only that proportion of the shock.
5.4.3 Next steps on gravity model and forward linkages of the dyadic trade
The most basic form of the gravity equation in IFs includes a limited set of driving variables (see again Table 5.3). Gravity functions in other models can include a number of additional explanatory variables, most commonly border contiguity, common language, and colonial history. It would also be useful to include regional or broader free trade agreement membership and the existence of a common currency. Inclusion of regional trade agreements and other political arrangements would open the door for some very interesting work involving two-way relationships with measures from the Pardee Center’s Diplometrics project. For instance, some recent studies have found a strong and significant influence of diplomatic representation on trade.[10] Threat level among countries is a strong candidate for inclusion.
If such varilables were added, parametric control of them would be useful. Also parameterized coefficients for the gravity equation variables could be useful―those parameters in Tables 5.4 and 5.5 are currently changeable by the model user via the Scenario Analysis/Change Selected Functions/Multivariate Functions window but not as model parameters in the scenaro parameter tree.
5.5 Forecasting of Other Bilateral Economic Flows in IFs
Table 5.2 showed an extensive list of bilateral variables in IFs of which three (trade, FDI, and foreign aid) have clear relationship to the social accounting structure of the IFs economic model. Of these, only trade is extensively developed.
The representation of FDI uses a simpler gravity model driven by only GDP and distance, a placeholder formulation upon which future work can be built. The representation in IFs of foreign aid as net inflows to countries complicates the development of bilateral dynamics and at this point only again a placeholder formulation is in place prior to possible movement of foreign aid to a gross representation (in reality, most countries are either donors or recipients and not both, making the net representation not so terribly different from gross values).
As Table 5.2 suggested, both FDI and foreign aid should be constrained as well as directed, just as trade is. Initial formulations in IFs treat them that way. Those interested in the non-economic bilateral variables of Table 5.2 are directed to other documentation on them.
5.6 Forward Impacts of Bilateral Economic Flows
Many possible forward linkages from bilateral projections (especially their impacts on other collaborative or conflictual interstate interactions) can be structured. Those have begun to be shaped within the IFs system. The most significant and extensive example is in the computation of an index called Formal Bilateral Influence Capacity (FBIC).
FBIC has two dimensions. The first is the Bandwidth countries have to influence other countries overall (such as the overall level of their alliances, membership in IGOs, volume of trade, and trade agreements). The second is the Dependence that influenced countries have on the influencing countries (such as the share of foreign aid that influenced countries receive as a portion of their GDP and the ratio of trade with an influencing country to the GDP of the influenced country.
The ratios to GDP in influenced countries of aid received from and trade volume with an influencing country are easily calculable from the dyadic representation of aid and trade flows. Those ratios constitute 21 percent and 28 percent, respectively, of the total Dependence side of the FBIC index (aid from an influencer as a portion of total aid received adds another 12 percent) (Moyer et al. 2021: 27). Other variables identified in Table 5.2, notably dyadic arms trade are also important in the calculation of the FBIC, but are not accounted for explicitly in the social accounting matrix structure of the IFs economic model.
For an analysis of the future of international relations using the FBIC see Moyer et al. (2018). As indicated earlier, Prazeres, Bohl, and Zhang (2021) use alternative scenarios of Latin American trade patterns to analyze the potential for differential political relationships of the region with China and the United States, while Kabandula, et al. (2020) use the representation of tariffs in the gravity model to analyze potential for success of the African Continental Free Trade Agreement.
5.7 Using the Dyadic Displays
Analyzing dyadic/bilateral data and forecasts is facilitated by two displays available in the IFs system. Because dyadic analysis within IFs began with analysis of historical data, in IFs version 7.82 both are found under the Data Analysis main menu option rather than under the Display option. Appendix A provides some information on their structure and use.
6 Labor[11]
Long-term, multi-sector economic forecasting benefits greatly from long-term forecasting of the quantity and skills of workers in the labor force and the demand for them (Fields 2005 and Basu et al. 2016). Production functions like the Cobb-Douglas equation used in IFs require attention to labor, but representation of labor is also related to the distinction between the formal and informal economies, to income distribution, and to poverty, all important in the IFs economic model and analysis with it. This section focuses more purely on the IFs treatment of supply and demand for labor and on their equilibration.
On the supply side, the total labor quantity term in IFs is responsive to two primary drivers:
- The age-sex structure of the population. In earlier versions of IFs, the working-age population was sometimes defined as 15-65. But for some time, IFs has followed the International Labor Organization’s (ILO’s) attention to the entire population 15 and older (ILO 2022a and ILO 2022b). With increasing numbers of healthy people above the age of 65 we can expect increasing numbers of workers in that age category. GTAP employment and wage data, which are used in IFs, come from the ILO Yearbook of Labour Statistics (see Weingarden and Tsigas 2010) and thus also pick up that age-range of workers. See Appendix A for extended discussion of labor data used in IFs and its preprocessing for the model runs.
- The participation rates of females and males in the formal work force. In most societies those of females are lower than those of males but have been rising; future rise in lower-income countries is of special interest. Rates for males are also changing, again including those for those 65 and older. Like IFs, which draws upon labor force and labor force participation rate data from the ILO, many sources of long-range forecasting use the current or relatively near-term projections by the ILO of participation rates (e.g. Chateau et al 2012 and Dellink et al 2017 with the OECD’s ENV-Growth and ENV-Linkages models). The World Bank’s Long Term Growth Model (LTGM) uses GTAP and therefore indirectly ILO data (Pennings 2020). ILO participation rates can be applied to many alternative population forecasts, including very often those from IIASA (Lutz and KC 2014).
Longer-term economic models and other quantitative analyses involving labor tend to be heavily supply-driven and to focus on the contributions of labor supply with limited if any attention to labor demand. For instance, an OECD outlook to 2060 (Johansson, et al. 2012) focused attention in the context of analysis of production factors on changing demographics, changing participation rates, and uncertain productivity, not at all on the demand side for the economy or labor. OECD work on the SSPs (Chateau, Dellink, Lanzi and Magne 2012) used the ENV-Growth model to 2050 and 2100, focusing again only on the supply side. Work with ENV-Linkages appears to do the same, although Chateau, Dellink and Lanzi (2014: 17, 37) show a demand for labor function (inversely related to wages) and suggest attention to labor displacement from mitigation policies while saying that “The calibration of these model extensions is, however, deemed not robust enough to be incorporated in the core version of the model.” WorldScan (CPB 1999: 26-31) forecasts out to 2050 and makes both labor supply (skilled and unskilled) and unemployment exogenous (linked as seems common to an assumption of the “natural rate” of unemployment), although it represents a formal/informal distinction (informality in agriculture and services) with movement of labor to the formal side and associated reduction of the unskilled labor share.
IFs does, however, devote considerable attention also to the demand for labor. The most important aspect of demand representation in IFs is not its total level and thus the potential for estimating unemployment (although the model does treat that), but rather the distribution of labor demand across sectors of the economy. Among the reasons for the importance of that distribution are two:
- The changing relative demand for skilled and unskilled workers as labor moves from predominantly rural employment to that in other sectors where the demand for skills is greater, at least in the earlier stages of development (farmers in economically advanced societies can be highly skilled). This changing pattern of demand in interaction with changing supply of skilled and unskilled workers has implications also for the distribution of income and the level of poverty calculated in IFs (documented in a later section).
- The differential productivity of labor across sectors, so that the movement of it from agriculture (in particular), which is often earlier in development processes very labor-intensive and poorly compensated, to sectors where workers typically produce a higher value of goods and services; this also affects overall economic growth rates.
In IFs, changing GDP per capita levels are key drivers of the changing patterns of demand for labor across sectors to which the supply of labor can be directed. But labor movement into non-agricultural sectors can also be constrained by urbanization rates, a constraint that the model represents. The constraint is not complete, of course, because rural populations can work in cities and vice versa (Tiffen 2003). Liu, et al. (2015) studied the relationship of urbanization and employment in China where the migration process has been very rapid. In addition to the relationship between urbanization and labor pattern change across sectors, they emphasized the relationship with the size of the informal sector, noting that in 2010 over 50 percent of population was rural and perhaps nearly 30 percent was in the urban informal sector. Their analysis looked back to early work on rural-urban migration, wages rates, and unemployment by Harris and Todaro (1970). Liu and colleagues presented three scenarios, including a middle-income-trap scenario in which rural-urban incomes failed to narrow and a significant percentage of Chinese population was still rural or informal urban even in 2050. The next major section of this documentation will return to the drivers of informality and its implications for economic development.
Turning more directly to the relationship between labor supply and demand, several elements of equilibration of total supply and demand could merit attention. One such aspect is choice by workers concerning the number of hours worked. Maynard Keynes famously forecast in the 1930s that the work week might decline in his grandchildren’s era in many countries to 15 hours. Partly related to the obvious difficulties surrounding any such forecast, IFs does not represent hours worked.
More generally, underemployment (including working fewer hours than desired) and unemployment of labor also are elements of the extent of employment. Although the ILO has given attention to underemployment (Hussmanns, Mehran, and Varmā 1990), neither it nor unemployment are typically calculated endogenously in long-term labor modeling. That is not surprising because it is difficult, for example, to imagine any real confidence in forecasting either, for example in Chad in 2047. In fact, in a study focused on OECD countries using stock-flow analysis, Barnichon and Garda (2016) defined their unemployment forecasts for the short-term and long-term as 3 months and 1 year, respectively.
IFs does, however, include a representation of unemployment in its labor model, as a mechanism for considering the general balance between the forces that generate labor supply and demand and as a way of getting some sense of the relative pressure for or surplus of skilled and unskilled labor subcategories. The model represents the equilibration in two different ways depending on analytical aims of the user. The first gradually moves unemployment rates from initial data-based values to a long-term target value; the second represents the changing balance between supply and demand sides of the labor model, thereby endogenously computing unemployment, but still gradually moving the rate to target values.
The subsections that follow focus in turn on labor supply, labor demand, and the equilibration of total supply and total demand. They conclude with notes on the forward linkages of the labor model, including a bridge to discussion of the informal economy linkage. Throughout this section we use subscripts and notations common to other modules of IFs (see Box 2.1). For example, we use t for time period. Subscripts p and r represent sex and country/region, respectively; c is the cohort number, with cohort 0 representing newborns, cohort 1 for the one-year to four-year-olds, cohort 2 for the five-year to nine-year-olds, etc. Values in the code for p are 1 for male, 2 for female (with the ordering reversed in the display forms of IFs) and 3 for both sexes combined. For economic sectors we use s and for skill levels sk.
- ↑ Globally, data in IFs underlying the first model year’s revenue-expenditure balance suggest that governments run an annual deficit or net dissaving of about 5 percent. Given a total national savings target of about 25 percent this would also reinforce the need for 30 percent savings by households and firms.
- ↑ See https://www.cia.gov/the-world-factbook/countries/timor-leste/#economy.
- ↑ The SeriesExportGoodSer% table has a long data series for Puerto Rico with values very often in the 60-70% of GDP range; SeriesImportGoodSer% is also long with values mostly in the 40-50% range. The CIA’s World Factbook similarly reports that the merchandise trade surplus reflects exports about 50% higher than imports and that Puerto Rico has a current account surplus of about 10% of GDP.
- ↑ David Bohl led the construction of the bilateral representation of trade and other interstate flows within IFs, in interaction with José Solórzano. Bohl also initiated and co-authored the documentation provided here.
- ↑ The gravity model has been considered one of the most successful empirical models in economics. Most applications aim to better understand the impact of various determinants of trade or to evaluate the effect that particular policy choices (e.g. joining a currency union or signing a trade agreement) may have on trade prospects, but some studies have used the model to forecast bilateral trade patterns in the medium- and long-term.
- ↑ Bilateral trade works in IFs with 188 countries, but not when countries are broken into provinces, districts, or other sub-units.
- ↑ As of version 7.82 there is a parameter to drive the model with bilateral trade, but when activated model behavior is poor, so it should not be used at this time.
- ↑ For information on the 2021 version see http://www.cepii.fr/CEPII/fr/bdd_modele/presentation.asp?id=37. The database covers 5000 products across 200 countries.
- ↑ Bilateral trade variables represent both total exports (XDYAD) and imports (MDYAD) as well as exports and imports by sector including agriculture (XDYADAGR and MDYADAGR), energy (XDYADENE and MDYADENE), ICT (XDYADICT and MDYADICT), manufactures (XDYADMAN and MDAYDMAN), materials (XDYADMAT and MDAYDMAT), and services (XDYADSER and MDYADSER).
- ↑ See Chapter 10 in The Gravity Model in International Trade (Afman, and Maurel 2010).
- ↑ Mohammod Irfan did initial development work on the labor model in IFs; Barry Hughes built heavily on that work.
6.1 Labor Supply
The total labor supply (LAB) is ultimately computed by multiplying the total population across working age categories (15+) with the total labor force participation rate (LABPARR). Those total population values for working age population and labor force participation rate are built up from dynamic age- and sex- specific foundations across the forecast horizon.
Population forecasts come from the IFs demographic model, which computes sex-specific age distributions across both five-year (for display purposes) and single-year (for model dynamics) age-sex categories (AgeDst, FAgeDst). Thus, the focus of the labor model documentation here will be on the determination of participation rates by country/region and gender.
Theoretically, it would have been possible to also specify LABPARR by age category, rather than only by country and sex. IFs took such an approach to elaborating poverty (see Section 9.2), albeit across 10 age categories rather than 5-year or 1-year categories as for population. In reality, that approach would be very complex to initialize and forecast for all 188 countries. Nonetheless, the calculation of LABPARR must be sensitive to changing age distributions, as well as to sex.
Therefore, for each sex total population participation rates in the model move with changes in the demographic composition, generally decreasing somewhat with the growth of population shares above 65 years of age (for which participation is lower than it is for the population between 15 and 65). Female participation rates in the formal labor force, which have historically been lower than those for males in almost all societies, but have moved up very significantly in most modern and affluent societies, get a catch-up boost in the model, particularly for economically less-developed countries. Further, when supply-demand labor equilibration is turned on in the model with the parameter labmarketsw set to 1 (it is 0 by default), participation rates by sex can also change when there is overall labor shortage or surplus and employers incentivize or discourage workers by changing wage rates.
6.1.1 Labor participation rate and active labor force
Labor participation rates (LABPARR) for males and females are first initialized for the model base year from historical data in the preprocessor (see Appendix A for details on the database).
In years after the first, a “catch-up” boost is added to the female participation rate. The annual boost added (driven by the term FemParLabMul) starts at half of a percentage point when that variable’s value is 1 and diminishes as the female rate approaches a catch-up target (FemParTar). That target across the horizon of the model is the minimum of the initial male participation rate and thirty percent above the initial female participation rate. If the female rate in the first year exceeds the male rate (only slightly the case for three African countries in model version 7.95), it will continue to do so over time in the same ratio.
In years after the first, a “catch-up” boost is added to the female participation rate. The annual boost added (driven by the term FemParLabMul) starts at half of a percentage point when that variable’s value is 1 and diminishes as the female rate approaches a catch-up target (FemParTar). That target across the horizon of the model is the minimum of the initial male participation rate and thirty percent above the initial female participation rate. If the female rate in the first year exceeds the male rate (only slightly the case for three African countries in model version 7.95), it will continue to do so over time in the same ratio.
where
Next, we compute and apply the aging impact on the participation rates of both genders. As the relative share of people over the retirement age has increased in higher-income countries, the participation rate of all those over 15 in age has declined. The model keeps track of the changes in the demographic pattern of the population who are in their prime working age of 15 to 64 (POPWORKING) relative to those at a common retirement age of sixty-five or older (POPGT65). Roughly speaking in the U.S., 75-80 percent of those between 15 and 64 work and only 15 percent of those 65 and older work.[1] Table A2 in Loichinger (2015) suggests that in 26 European Union Countries the numbers are closer to or somewhat above 80 percent and 5 percent, with an expectation that in 2053 it will be moving toward 8 percent above 65 years of age. Although it would be ideal to have data-based numbers across all countries and time, the U.S. values can serve as a rough indicator of labor distribution patterns for an age-category sensitive scaling factor (LaborAgeScaleFac). Comparing that scaling factor in any year with the initial condition of it for a country can give us an aging impact multiplier (Aging_Impact) for modification of the participation rate based on first year data. This ratio will decline as countries age.
where
It is important to note, however, that POPWORKING, the population of working age, is defined as the number of people between 15 and 64 years of age only in the model’s default logic when the age of entry into the work force (workageentry) and the retirement age (workageretire) are set at default values of 15 and 65. The calculation of POPWORKING is done in the population model and alternative parameter values are possible in scenarios. If the retirement age parameter value is changed, the term POPGT65 in the above equation should be adjusted accordingly, but the code does not do that as of Version 7.95.
The participation rates of the base case can also be changed by a model user through two model parameters: a direct multiplier on the participation rate (labparm), or one that the user may identify as representing changes in participation resulting from changes in the retirement age (labretagem).
When the endogenous balancing of labor supply and demand is turned on (labmarketsw=1), it generates a non-zero and temporally changing labor wage index (LABWAGEIND) index to be described in a subsequent subsection. A smoothed value of that over time becomes a labor wage impact variable in the model (LabWageImpact) and participation rates respond slowly to it (and therefore causally to unemployment rate). When such endogeneity is active, the equation above is replaced by that below:
where
Total participation rate across sexes (LABPARR (p=3)) is computed by a population category-weighted average of male and female participation rates. The age category variable from the population model is AgeDst.
6.1.2 Labor participation rate and supply: Legacy approach
In very early versions of IFs a different concept of the labor participation rate (LAPOPR) as the ratio of the labor force (LAB) to total population was driven exogenously. Over time it was elaborated so that like LABPARR it is affected by both the female participation rate and the age structure of the population, including that aged 65 and above. This subsection documents LAPOPR because it is still computed even though it now has no forward linkages and has been replaced in forward dynamics by LABPAPR.
The participation of women in the work force (FEMSHRLAB) as a share of the total labor force was assumed to grow over time with an exogenous parameter based on past experience (femshrgr); the representation of women as a share of the total labor force of both women and men, rather than in terms of percentage points of participation of working-age women, somewhat complicates the equations below. The growth in labor-force share is modified by a multiplier (FemShrLabMul) that introduces saturation as female participation rates approach a target (FemShrTar). The model user can generate that saturation target, normally between 50 and 60%, adjusted via an exogenous parameter (labfemshrm).
The calculation of LAPOPR relative to its value in the first model year is affected also by the aging of the work force, now using the same scaling factor (LabAgeScaleFactor) as in the calculation of LABPARR.
Change in the retirement age can be roughly reflected in the above equation via a multiplicative parameter (labretagem).
When LAPOPR was actively used, the product of it and POP provided the total labor pool (LAB). At this point LAPOPR is informational only as an alternative approach to calculating the gender-specific participation rate (LABPARR) over time. The behavior of it is quite similar to total LABPARR, but its values are considerably lower because it represents workers as a share of total population rather than as an age-adjusted share of working age population. It no longer has forward linkages.
6.2 Labor Demand Equations
The IFs economic model forecasts production and therefore also labor demand in six economic sectors – agriculture, energy, materials, manufacture, services and information and communication technology. The IFs labor model computes demand for skilled and unskilled labor (LABDEMS) in each of the sectors.
6.2.1 Sectoral labor demand evolution with economic development
The foundational long-term driver of labor requirements is technological progress associated with economic development. With economic and therefore implicitly also technological advance, the demand for both unskilled and skilled workers per unit of output tends to decrease and the balance to shift toward skilled workers. Figure 6.1 illustrates this by plotting changes in unskilled and skilled labor requirements in agriculture and manufacturing sectors against GDP per capita at PPP, a proxy for level of development. While agriculture is much less skill-intensive than manufacturing, with economic and technological progress the relative need for skilled workers increases rapidly in both sectors. The IFs labor model computes these labor requirement functions in the model preprocessor using GTAP data on employment by occupation and economic activity (see the labor model section of Appendix A for a mapping of sectors and occupations between GTAP and IFs).
These cross-sectionally estimated functions (LaborF) for each sector and skill type are used to compute labor coefficients (LABCOEFFS), i.e., number of skilled or unskilled workers needed to produce a unit of output in any given sector. The subscript s stands for the economic sectors in IFs, and the subscript sk stands for skill categories with 1 denoting unskilled and 2 skilled. Because GDP per capita at PPP (GDPPCP) is not yet calculated at this point in the flow of the model, the value from the previous time step is used.
IFs can make two adjustments to the coefficients produced by the cross-sectionally estimated functions (shown here as LABCOEFFSFromFunction – in the code the variable name above and below on both sides of the equation is simply LABCOEFFS). Most simply, model users can use a global parameter (labcoeffsm) to change the labor coefficients by skill level for any or all of the six sectors.
The more complicated adjustment above is the calculation and use of the labor coefficient adjustment factor (LabCoeffAdjFac). Fundamentally, it is a recognition that while the cross-sectionally estimated functions for the coefficients should quite well represent long-term changes in the labor coefficients with GDPPCP, shorter-term shocks to GDPPCP like those in the COVID period might not affect labor demand in the same way and could quite possibly have less impact on the labor demand; for instance in the long-term, GDPPCP change carries with it technological change that is much less likely in the short-run. Rather than setting up early forecast period disconnect between the two variables, particularly when the exogenous use of GDP series in early model years can create bumpy exogenous GDP growth rate specification, the adjustment factor is computed in year 2 as a function of the relationship between the corrected longer-term economic growth rate (igdprcor), the change in labor force size (LAB), and the change in the estimated labor coefficients. The adjustment factor convergences to 0 over 10 years after the model has completed its passage through the period of those early-year exogenous economic growth rate changes, including irregular patterns associated with factors such as the COVID-19 epidemic. Overall, this smooths the pattern of labor force demand because that pattern seldom changes as rapidly as does the economic growth rate.
where
6.2.2 Labor demand adjustments
If everything at this point were simple, the model could move to a calculation of labor demand by multiplying the coefficients times value added (VADD) by sector and a scaling factor of 1,000 because value added is in billions and labor demand is in millions.
Unfortunately, there are several complications to be addressed that significantly complicate the simple (and not used) formula above, leading instead to the one below. Most basically, value added calculations in each time step require labor by sector (LABS) and they follow rather than precede the analysis of labor demand and its relationship with total labor supply and its allocation across the sectors of demand. Hence, VADD, GDP and GDP per capita are also not yet available in the model flow; an estimated value added is computed by using the corrected long-term GDP growth rate (igdprcor), computed in the first model year, to increase the lagged value. The more fully elaborated equation for LABDEMS is the one below using VADD from the previous year with several additional adjustment factors.
The second adjustment shown above uses RemoveAgEnExogGr to back out of the labor coefficients the impact on value added of exogenous interventions that change agricultural yield and energy production in the two respective partial equilibrium model determinations of value added. Such exogenous change in yield (using the parameter ylm) and energy production (using enpm) is assumed in most scenarios to be technologically driven and therefore should not affect the labor requirements of value added in those sectors. The variable name RemoveAgEnExogGr is not actually used in the code (but probably should be); it represents in the equation above the result of algorithmic calculation for that backing out of exogenous impact by dividing the sector labor coefficients by the ylm and enpm parameters used in the agriculture and energy models.
Other adjustments include:
- The use of the labor wage impact multiplier (LabWageImpactMul), the calculation of which is explained in the equilibration section of this labor model documentation, see Section 6.3, especially 6.3.3.1. The multiplier it is responsive to the disequilibrium between the values of unemployment-adjusted total labor supply and demand and therefore only is used in the labor demand equation when the endogenous labor market switch (labmarketsw) is turned on); by default it is off and he value of the multiplier would be 1.0.
- The exogenous multiplier of labor demand by sector, although not by skill level as is allowed with the labor coefficient multiplier (labdemsm).
Finally, the adjustment factor (LabDemsAdjFac) is computed as the ratio in the first year between the actual and computed employment by sector. Actual employment in the model’s first year is obtained from historical data (LABEMPS) processed using the GTAP database. The computed employment is obtained by multiplying the labor coefficients (LABCOEFFS) with the output of the sector (VADD). Clearly, the labor coefficients computed from cross-sectional functions will not precisely generate the level of total employment that we find in the data. In IFs we often refer to the adjustment factor needed to reconcile data and computed values in the first year as a shift factor. Contrary to much practice in IFs, this multiplicative shift factor in labor is not converged to a value of 1 over time but assumed to represent persistent national differences in economic sectoral structures.
6.2.3 Agricultural labor demand adjustment associated with urbanization
Given the initial calculation of labor demand by sector and skill level, there remains still another adjustment of importance. IFs represents urbanization in the development process (documented with the population model). Historical data for the shares of population in rural and urban areas is quite extensive for many years across most countries and the IFs Base Case forecasts of them are quite well behaved as continuations of those historical series. The data on historical labor in agricultural are much less complete and, unfortunately, forecasts of demand for agricultural labor using the demand equations discussed above, while exhibiting the declines as share of total labor demand that one would expect across time and economic development levels, can differ substantially in slope of that decline from those generated by the IFs forecasts of shifts in population from rural to urban areas.
Therefore, a structure was added to IFs that computes the proportion of population that is rural and the proportion of total labor demand that is agricultural. Algorithmic formulations constrain changes in and absolute levels of agricultural labor demand’s share of total labor demand in two ways:
- Annual percentage change in the labor demand share of agriculture is limited to no more than 20 percent (not percentage points) more than a moving average rate of change in the share of rural population within total population.
- When the agricultural share of labor demand in the base year exceeds the rural population share of the total in that year, the algorithm slowly converges over time the evolving agricultural share computed using the labor demand coefficients to the evolving rural population share. Therefore, by the end of the century, no country in IFs has a significantly higher share of labor in agriculture than it has in rural areas, consistent with the argument by Tiffen (2003: 1350) and the general expectation that employment of urban dwellers (truly urban not small town or farmer village residents) in agriculture is almost always less common than employment of rural residents in cities.
When the share of agricultural labor demand in the base year falls short of the share of rural population, these logics do not prevent some upward movement of agricultural share over time and perhaps they should. Yet, given the “back to the countryside” impetus in some countries, such a rise in agricultural labor share may be possible, and given relatively poor data on labor across sectors, such a pattern in the base year might indicate an under-estimate of the actual agricultural share of labor demand. In any case, such a rise appears in few countries and, if desired, can be prevented via scenario analysis.
When adjustments are made to LABDEMS for agricultural labor in this urbanization- related adjustment process, the numerical value of those adjustments is offset in all other sectors proportionally to the earlier calculation of their labor demand.
6.2.4 Protect agricultural labor against disruption from exogenous GDP
The cross-sectionally-estimated functions that compute labor demand evolution with GDP per capita help change those demand patterns with the steady advance of economic development. Sudden and very large changes in GDP resulting from conflict or disruptions like those from COVID-19 will inevitably result in some shifts of labor across sectors, but they do not represent those same longer-term development patterns and should therefore not normally change demand across sectors nearly as much. In the early years of IFs forecasts the use of the parameter that exogenously represents GDP growth rate (gdprext) often introduced such sudden changes in GDP; for instance, in the 2010-2020 decade both Venezuela and Libya experienced them, and in 2020-2022 many countries experience them because of COVID.
An algorithmic structure dampens changes in labor demand patterns in response to dramatic GDP per capita changes. Specifically, it limits year-to-year increase in the share of agricultural labor within the sum of all labor demand to 5 percent or less; it further limits increase in that agricultural share to 10 percent or less of the value in the base year. The implicit assumption is that the GDP growth rate shocks from such disruptive events are for the most part directionally downward. The absolute adjustments to agricultural labor demand to stay within these parameters are allocated proportionately to the labor demand in all other sectors.
6.3 Unemployment and Wages: Labor Market Closure/Equilibrium
6.3.1 Overview
There are two alternative approaches to closure rules in IFs for balancing labor supply in total (LAB) and the sum of labor demand across economic sectors and skill levels (LABDEMS), recognizing that there will always be some rate of unemployment (LABUNEMPR). The default approach (when labmarketsw is 0) directly sets unemployment rates in each year of the model runs; it normalizes the labor demand across sectors and skill levels to the labor supply minus that unemployment rate. The other approach (when labmarketsw is 1) endogenously computes unemployment by activating a dynamic equilibration process; the model chases a target value across time.
In both approaches movement from base year unemployment rates toward a specified ultimate unemployment target value (LabUnEmpRateTarget) is phased in over a specified number of years (labunemprtrgtyr). A linearly changing interim target value (LabUnEmplTar) is computed through convergence across those years of the base year’s unemployment rate (LABUNEMPRi) to that specified ultimate target.
where
The specification of the ultimate target value for unemployment rate (LabUnEmpRateTarget) can be done in one of two ways. The first is exogenous specification of it using the parameter labunemprtrgtval. Any non-zero value of that parameter identifies the ultimate target:
But the default value for labunemprtrgtval through at least IFs version 7.95 is 0.0. When that is the value, the ultimate target value is set by the model to be the lesser of the country’s unemployment rate in the base year or 10 percent. Many countries have data values above that level in the base year.[2]
The two approaches use information from the interim target value (LabUnEmplTar) to precisely determine or gradually shape annual calculation of labor demand. The approach driven fully by the interim target feeds it directly to labor demand, normalizing the results from the earlier labor demand analysis (see again Section 6.2) to the labor supply minus that target value. The PID equilibration approach applies a multiplier variable to labor demand that is assumed by name to be implicitly responsive to wage changes (LabWageImpactMul). In demand-side model elaboration it has, however, proven more efficient to drive the variable simply by the disequilibrium between targeted unemployment rate and that computed from comparing the labor supply and demand values.
In both approaches the final value for labor demand by sector and skill level is ultimately also put into a variable named labor employed (LABEMPS). That variable is taken to the computation of household earnings by skill level (Section 3.2), despite an imperfect match between skill levels as an individual worker characteristic and household categories which might, in reality be made up of adults with different skill levels (implicitly, household categories are being designated by the skill level of the most educated member).
6.3.2 Labor market closure with normalization to target unemployment
When the labor market switch parameter (labmarketsw) is set to zero (the default), it means that the model user wishes to drive with precision each country’s unemployment rate from initial conditions toward the target value as determined by labunemprtrgtval over the specified period (labunemprtrgtyr). To repeat: when the target value parameter (labunemprtrgtval) has the value of zero, the model sets the ultimate target value as the smaller of the country’s base year value and 10 percent.
If precise unemployment-target reaching is to occur, the values of labor demand across all sectors and skill levels must be normalized to the total labor supply minus the unemployment determined by the evolving target rate of unemployment across time (LabUnEmplTar). The normalization equation is
6.3.3 Labor market equilibration
The equilibration approach turns on dynamic rather than automatic labor market equilibration when the switch labmarketsw set to 1.0. It uses a PID-like controller algorithm, similar to those of other stock-flow equilibrations in the economic model (see Section 4). When the labor market is activated, the unemployment rate (LABUNEMPR) is computed as an endogenous representation of disequilibrium between supply and demand, and the algorithm looks to that unemployment rate in comparison with the temporally specific target level (see Section 6.3.1) for adjustments to labor demand as described earlier in Section 6.2 and to a lesser degree to labor supply as described in Section 6.1. The equilibration process in the IFs labor model thus algorithmically chases balance in the labor market rather than computing a precise equilibrium in each time step.
6.3.3.1 Labor market equilibration algorithm
In earlier versions of the labor model, an elaborated PID approach was used, focusing the PID on the distance between the unemployment rate (LABUNEMPR) and the target value for unemployment (LabUnEmplTar) and the changing of that distance across time. It was found that more direct control could be introduced by simply using the absolute integral difference term (Diff1) of the PID approach rather than also the second order or year-to-year change in difference term.
Specifically, an employment gap (EmplGap) is computed as the difference between labor supply (LAB) and the sum of labor demands (SumLD).
where
Given that employment gap, an initial calculation of the unemployment rate (LABUNEMPR) can be made. It is initial in that the employment gap could even be negative if labor demand exceeds supply. This initial value is used to compute the Diff1 term in comparison with the temporally changing labor unemployment target as described earlier even if the unemployment rate is negative, because allowing that provides the clearest signal back to the labor demand and supply coefficients in the pursuit of equilibrium.
After computing that signal the unemployment rate is bound for reasonableness including elimination of negative values, and it is converted to percentage terms.
The difference term is used to adjust a multiplier (Mull) that uses and then updates a cumulative term for the multiplier across time (MullW), constraining the year-to-year change in the annual multiplier and therefore also the cumulative term. That is, the equations below use the logic of the PID approach without a call to the ADJSTR function more often used in its implementations (as in Section 4.4)
The cumulative multiplier is carried forward in time (as LabWageImpactMul) and, in the next time cycle will alter the multiplier used to adjust the demand-side labor coefficients, helping keep the supply and demand calculations roughly in line by controlling the pursuit of equilibrium around the evolving labor unemployment target.[3]
It is important to emphasize, however, that the pursuit of equilibrium when the labor market switch (labmarketsw) is set to 1.0 does not ever precisely achieve it (although after the interim target stabilizes at the ultimate value it can come close to doing so). The extent to which the actual unemployment deviates from the target value helps us understand the degree to which countries might be likely to experience supply-side or demand-side forces that will, in fact, often lead to higher or lower unemployment rates. For instance, the increasing demographic dividend of many lower income countries is already boosting their labor supply faster than economic growth typically increases labor demand; because that dividend in many countries is set to grow further, the likelihood of persistently high unemployment (or growth in informality) in those countries is substantial. Such insight can be useful even if any specific forecast of unemployment rates has limited credibility.
6.3.3.2 Labor wage index
Upward movement of unemployment (and potentially of informality levels) would reasonably be expected to push down wages, just as a shortage of labor supply relative to demand would push them up. As an indicator of these forces the model computes a labor wage index (LABWAGEIND) that responds, as does the cumulative labor demand coefficient multiplier (LabWageImpactMul) discussed above, to the difference between the evolving unemployment target level and the computed unemployment rate.
In an earlier version of IFs, this wage index used a full PID controller logic for its change over time. Also, it was the carrier of the feedback from unemployment rate disequilibrium to the labor wage impact multipliers (LabWageImpactMul and LabWageImpact) and to the labor demand and supply sides of the model. Further, that feedback from the wage index was linked to the labor demand impact via a second PID controller. As the labor market representation has evolved, it became obvious that it was very difficult even to reasonably scale the change in wages to the unemployment rate, much less to use that as a driver of labor demand coefficients. Hence, the structure was simplified, and the labor wage index now does not affect the demand side of the model but instead is used as described earlier to modify the labor participation rate on the supply side. That modification is done via the internal variable LabWageImpact, with smoothed and relatively slow changes in response to changes in LABWAGEIND.
6.4 Forward Impacts of Labor Supply and Demand Calculation
6.4.1 Labor supply by sector: Bridge to production function
The IFs production function combines capital, labor, and total factor productivity to compute value added by sector. It does not distinguish in that function between labor by skill level within each sector. The labor variable used in the function is LABS, simply the sum of labor demand across skill levels.
6.4.2 Labor by Skill Level: Bridge to Income Distribution
Labor supply by skill level (LABSUP) is important in the analysis of income distribution and poverty levels (discussed in Sections 8 and 9) when it is examined relative to the income received by skill level. The labor model therefore forecasts labor supply (LABSUP) by two skill categories.
The equation set below for the value of labor supply in the skilled category is best understood as a sequence of five steps, described below in their order of computation in the model system:
- In the preprocessor a calculation of total base-year labor supply by skill category (LABSUP) is made by reading the employment by skill/occupation (LABEMPS) data from GTAP[4] and adjusting via division by the unemployment rate (LABUNEMPR). We assume the same unemployment rate (LABUMEMPR)for skilled and unskilled labor.
- In the first year of the model’s calculation those labor supply values are used to compute the initial ratio of skilled labor to total labor (LABSUPSkilledRI).
- In all years of the model run computations are made of the percentage of labor that is skilled (PerSkilled) by adjusting that initial value of the percentage skilled with changes in the average years of formal education that have been acquired by the population aged 15 and older (EDYRSAG15).
- A product of the evolving percentage of the labor that is skilled and the total labor force (LAB) provides the size of the skilled labor force each year.
- The unskilled labor supply is simply the residual.
Step 3, determining the percentage of labor supply that is skilled in any given year, is the big one. At the core of that calculation of percent skilled in IFs was long an analytical function with GDP per capita at PPP (GDPPCP). But that cross-sectionally estimated analytical function was fundamentally tied to conditions that prevail in the contemporary era (as captured by the GTAP data on which it was based). We know that education levels have been increasing, even to the extent of involving some credential inflation. Thus, the percentage of the labor force considered skilled is likely to increase more slowly than any cross-sectionally estimated function with either GDP per capita or years of education would indicate. Moreover, there is not enough historical data to really analyze what the credential inflation pattern might look like as the overall level of education across societies increases and, as in higher-income societies today, more highly educated individuals increasingly fill lower-skill jobs.
Therefore, an analysis of labor demand by skill level was done in the Base Case of the model across countries and income levels, and that analysis was used algorithmically (basically by trial and error) to create a function for the education inflation needed to be in the percentage skilled, so that the actual PerSkilled supply generally matches the pattern of skilled demand in the work force. As years of education rise to the value in the model’s base year, each point of increase can raise the portion of labor that is skilled by a maximum of 0.5 points. But it is reasonable also that the increase in skilled labor also diminishes as its percentage of the total labor force increases; the presumption based on examining data on the saturation of skilled share across countries is that as that share approaches 60 percent, the contribution of additional education steadily declines to zero.
where
and where in the first timestep
and where in the preprocessor
As indicated earlier, labor supply by skill is linked to income distribution and therefore also to poverty. Those linkages are elaborated in Sections 8 and 9.
6.4.3 Legacy Process 1 for Computing Labor by Skill Level
The approach for computing the portions of labor that are skilled and unskilled has evolved in IFs over time. Given the uncertainties of how best to forecast those, it is useful to hold onto some information about two legacy approaches to that computation, described in this and the next sub-subsection. Identification of the weaknesses of past approaches also helps explain the motivation for the current one.
All approaches to specifying labor skill in IFs have involved looking at the formal educational attainment levels of the adult population. The cross-sectional representation in Figure 6.2 shows the portion of the population 25 years and older with tertiary education plus ½ of that with secondary education. That is a very arbitrary and crude definition of skilled labor, but is one possible starting point―and analysis of change in the share of labor that is skilled is more important in the subsequent calculation of Gini than is the exact initial definition of the share. The value of tying the size of skilled and unskilled labor forces to education completion is that the education module of IFs forecasts sizes of population with various educational attainment levels and those can be driven by agent-class interventions. And it is the change in share of skilled labor that is most important, not the absolute numbers—the Gini coefficient data can be used to adjust the initial conditions of income distribution and the change in labor force sizes can help us forecast the change in Gini.
There are some obvious problems with Figure 6.2. One of the most significant is that better fits are achieved by other functional forms, including the logarithmic one in Figure 6.3. Unfortunately, those forms tend to suggest that the poorest countries have absolutely no skilled labor, clearly an exaggeration.
How do we know that an absence of skilled labor in the poorest countries is an exaggeration? In addition to common sense, it can be seen from the GTAP data on the income share of skilled labor in Figure 6.4. That shows that they obtain a substantial share of value added even at the lowest levels of GDP per capita. The two cross-sectional plots in Figures 6.4 and 6.5 show the shares of value added accruing to skilled and unskilled labor, respectively.
6.4.4 Legacy Process 2 for Computing Labor by Skill Level
The initial legacy procedure for computing skilled labor, used in IFs as input to the computation of Gini values, produced some unrealistic behavior, in part because there is credential inflation as GDPPCP, education, and technological sophistication rise; as countries become richer, fewer and fewer of those with tertiary education, much less secondary, are considered adequately skilled. Therefore, the model was switched to one that looked at the average years of education held by adults 15 years of age and over (EDYRSAG15), and a relationship was built that links that value to the percentage of the work force that is skilled, raising the bar to be skilled as GDP per capita at PPP rises.
The replacement forecasting process began by using a function estimated from the relationship between GDPPCP and GTAP data on the share of value added accruing to skilled workers to estimate the share of the labor force that is skilled (PerSkilled); that was known to be wrong, but remember that we do not need the exact share, what we need is the change over time. And the model used that same function over time to estimate the expected share of skilled labor, all else equal, over time. But all is not equal and it is unequal to the extent that education levels rise higher than those that we would expect in the same development process. Hence there was an adjustment term in the calculation (LabSupSkillAdj) that looked at the difference between the actual years of education in the population and the expected years (YearsEdExp), again computed by an analytical function with GDP per capita at PPP. A fraction of the proportional difference of actual with expected was added to the percentage skilled.
where
Given the percentage skilled it was simple to calculate the number skilled (LABSUP) and the residual percentage of the labor force that is unskilled.
This process, with its two analytical functions, was ultimately deemed to be unnecessarily complicated and the Pardee Center moved to the current, simpler process described earlier.
6.5 Informal Labor
IFs forecasts informal sector shares of labor and GDP. Informal labor is not, however, explicitly endogenized in the labor market elaboration of labor supply, demand, and unemployment that has been described in this Section 6. Instead, a submodel of informality was developed for IFs within which to forecast both informal labor and GDP. The next section documents that submodel.
7 The Informal Economy[5]
According to data from projects of the International Labor Organization and the World Bank, in emerging market and developing countries (EMDEs) the informal economy accounts for more than 70 percent of employment and about one-third of output (Ohnsorge and Yu 2021: xv). Although such levels of labor informality decreased by about 10 percent of employment between 1990 and 2018, they remain far above the roughly 16 percent in advanced/high-income economies (Ohnsorge and Yu 2021: 6)
Among the consequences of informality are lower productivity and reduced government revenues, important issues identified by analysts at least back to de Soto (1986). Hence representing informality in the economic model of IFs and the prospects for its reduction has very considerable importance. At the same time, however, such representation faces considerable challenges with respect to conceptualization and data that require elaboration.
The modeling of informality in IFs was initially structured in the context of a project of the Pardee Center with the Centro Nacional de Planeamiento Estratégico (CEPLAN) of Peru. A major report to CEPLAN (Bohl, et al. 2015; CEPLAN 2016) elaborates that foundational modeling considerably more than this section does. The documentation here draws from Bohl, et al. (2015) and brings up to date the current treatment within IFs.
7.1 Concepts, Measurement, and Data
We conceptualize the informal economy as having two interacting parts, informal labor and informal production. Also, we recognize a distinction in terminology and to some degree also in conceptualization, but especially in measurement/data, between the informal economy qua informal economy or non-observed economy and the shadow economy.
With respect to production, our primary conceptualization and measurement rely on the OECD’s non-observed economy (NOE) framework (OECD 2002), which includes underground production (legal but concealed from authorities), illegal production, informal sector production (from unincorporated enterprises in households for others), and production of households for own-final use, and a further underground of activities that escape data collection systems (OECD 2002: 13; see also UNECE 2008; Gyomai 2012 and 2014). There is close alignment of the NOE with the 1993 and 2010 revisions of the System of National Accounts (SNA), which ideally guides country reporting of all economic activity to the International Monetary Fund and others (UNECE 2008 and 2021).
Conceptually, the NOE framework aligns fairly closely with the shadow economy concept used by Schneider and Enste (2000) and others, although analysis of the shadow economy definitionally focuses somewhat more narrowly on legal market-based production of goods and services that are concealed from government authorities. It therefore can be surprising that production estimates from the shadow economy literature tend to be considerably higher than those from the NOE literature.
Both literatures are fully aware of the complications of measurement and of errors in it. To represent informality the United Nations Economic Commission for Europe (UNECE) has sought to use and enhance estimates of the adjustments that countries have done to measurement of GDP. UNECE (2008: Table 1 pp. 10-11) showed such adjustments for 43 mostly high-income and upper-middle-income countries. Such analysis is often done by national statistical offices based on information from surveys, but unfortunately instruments and analysis varies considerably across countries and they very often do not separately identify the informal portion. Both the International Monetary Fund (IMF 2021) and UNECE (2021) have emphasized the great need for improvements and extensions in such representation.
Shadow economy analysis and literature have recognized the tremendous measurement problems associated with the various elements of informality and have therefore relied heavily on estimation using a modeling approach named Multiple Indicators, Multiple Causes (MIMIC) that estimates an unobservable index with potential determinant and indicator variables, a form of structural equation modeling (SEM) or factor analysis (Almenar, Sánchez, and Sapena 2020).
As noted, despite the narrower definition of the shadow economy concept relative to the non-observed economy, quantitative values of the former from the model-based analysis are very often found to be larger than those of the latter from official reporting. A major reason for this is that the MIMIC approach and other modeling-based approaches provide useful information on likely changes in the size of the shadow economy over time, but they are not very useful for identifying the absolute size of it.
Instead, that literature looks to a single benchmark year’s value for each country and then scales other annual estimates around it. Because of the methodological challenges associated with the NOE-SNA approach and the small number of countries reporting informal adjustments to GDP, the shadow economy literature does not normally look to values from it for benchmarks. Most commonly, the literature uses instead a “Currency Demand Approach” that analyzes the currency in circulation to calculate the likely use of it to hide transactions (or to represent lack of access to non-currency-based transactions) and thereby the size of the shadow economy. First use is often attributed to Cagan (1958) with further development by Tanzi (1980, 1983).
For instance, Elgin and Oztunali (2012) built longitudinal shadow economy estimates for 161 countries 1950-2009. They drew upon Schneider et al. (2010) for shadow economy size benchmark estimates in 2007 (Elgin and Oztunali 2012: 16). Schneider et al. (2010) with values for 162 countries points in turn to Schneider (2007) with values from 145 countries. Both studies (Table 6.3, pp. 50-53 in the former) determined benchmark values using the currency demand method. Further, a major study associated with the World Bank (Ohnsorge and Yu 2021) used both a dynamic general equilibrium (DGE) model and DYMIMIC for analysis of the shadow economy in 160 countries across roughly 1990-2018. Both models drew upon Schneider et al (2010) for benchmark values in 2000 (see their Table 1a).
Given the continued push to enhance the SNA with survey-based and other focused empirical attention to the non-observed economy, it seems likely that national statistical reporting of the size of the informal economy will become increasingly strong relative to the use of the currency demand approach that has been so important to the benchmarking of the shadow economy. It also seems that the model-based analysis of the shadow economy literature will be essential to creating longer-term time series estimating production in the informal economy. The IFs project approach has therefore created a blended database, looking to the NOE data for benchmarking and to the shadow economy estimates to create a time series.
The foundation in IFs for the blended informal economy production database consists of four data series in the master datafile IFsHistSeries.mdb:
- GDPInformal%Adjustment: 40 countries 1995-2005 from Table 1 (page 10) UNECE’s 2008 publication “Non-Observed Economy in National Accounts: Survey of Country Practices.” Data for Peru to 2010 were added from INEI (2014).
- GDPInformal%Elgin: 160 countries 1950-2009 from Elgin and Oztunali (2012) at http://www.econ.boun.edu.tr/public_html/RePEc/pdf/201205.pdf. This file is used in the preprocessor to initialize the shadow economy variable.
- GDPInformal%Schneider: 161 countries 1999-2007 from Schneider, Buehn and Montenegro (2010), at https://documents1.worldbank.org/curated/en/311991468037132740/pdf/WPS5356.pdf
- GDPInformal%Blended: 165 countries 1960-2010 from UNECE (2008) and Elgin and Oztunali (2012); looking also to Schneider and Enste (2000); Schneider, Buehn, and Montenegro (2010), Buehn and Schneider (2012), andSchneider and Elgin (2012). This file is used in the preprocessor to initialize the informal economy variable.
The blending process for the fourth file above required adjustment of the MIMIC-derived estimates to bring them in-line with the size of the NOE estimates. We first plotted regression lines for the first two data series against the log of GDP per capita at purchasing power parity in USD 2011 (logged to create a linear relationship). The differences between the regression lines at each level of logged GDP2011PCPPP supported chaining countries that existed in both data sets to the available data from UNECE (2008) and from INEI (2014) for Peru alone. We set a hard lower limit of 1%.
More recent datasets for the shadow economy and informal labor are available from the World Bank’s Prospects Group at https://www.worldbank.org/en/research/brief/informal-economy-database. These cover up to 196 countries from 1990-2018. The production data are provided from two modeling approaches, both MIMIC and the Dynamic General Equilibrium (DGE) model. The edited volume of Ohnsorge and Yu (2021) describe the data and use it. Elgin et al. (2021) elaborates the modeling approaches and data.
Using these datasets the IFs system initializes and computes GDPINFORMSHR and GDPSHADOWSHR, the respective percentages of GDP in the informal/non-observed and shadow economy formulations. It also computes forward impacts of informality; for those, IFs relies on the informal economy variable by default, but the user can switch to driving those impacts by the shadow economy share.
Turning to informal labor, there is not the same differentiation of conceptualization and data as between the non-observed economy and shadow economy. But there are important distinctions across the populations for which informality is represented. Early definitions of the informal labor force were tied directly to previous formulations of the OECD’s non-observed economy framework, whereby informal labor was essentially the labor that worked for informal enterprises. In 1993, the International Conference of Labour Statisticians recognized that this enterprise-based definition failed to capture the vast heterogeneity of the informal labor force (ILO 2002). Since then, the International Labor Organization (ILO) and the Women in Informal Employment: Globalizing and Organizing (WIEGO) policy network have shaped the field in informal labor research. Central to their work is the collection and analysis of household surveys aimed at capturing the multidimensional nature of informality.
We follow the lead of the ILO and WIEGO to include not just informal labor employed within informal enterprises or self-employed, but also informal labor in the formal sector and (paid labor) in households Their statistical definition(s) of informal employment provides the framework for their creation of data that quantifies informal employment by employment relation, economic sector, and gender. Specifically, they make three distinctions of considerable importance (ILO 2013 and 2018; Chen 2012):
- In addition to informal labor being defined as labor that works within informal enterprises, there are two other categories of informality: informal labor within the formal sector and paid labor within households (without coverage by labor legislation and social benefits). In general, these two additional categories are very considerably smaller than informality in the informal sector, but by no means insignificant.
- The great importance of agricultural production in most less-developed economies and the importance of subsistence (and therefore informal) agricultural labor in that economic sector makes it a category of informality worthy of special attention and subject to somewhat different dynamics of change than informality in urban contexts. Most often, informality rates in agriculture are higher than in other sectors.
- Women and men differ in their representation across the various types of informality.
Having made these distinctions, the ILO now uses survey-based information to provide data across all of them. The representation of informality in IFs builds on that differentiation. Specifically, IFs initializes and computes three variables:
- LABINFORMSHR is the most general and is the percentage of total employed non-agricultural labor that is informal, regardless of type of informality and sex. Largely because of data availability, this variable represents informality only in non-agricultural sectors.
- LABINFORMPCNTINF (differentiated by sex) is the percentage of informal non-agricultural labor that works in informal enterprises.
- LABINFORMPCNTNONINF (differentiated by sex) is the percentage of informal non-agricultural labor that works in formal enterprises or households. The sum of this and LABINFORMPCNTINF is 100 percent.
To initialize these variables for the 188 countries in IFs, the preprocessor of the model system draws on several data series from ILO-WIEGO and the World Bank. The 2014 World Development Indicators (WDI) report cited the ILO’s Key Indicators of the Labour Market as the original source of its data on informality by gender. This suggests that the WB and ILO-WIEGO datasets (Bonnet, Vanek and Chen. 2019) are based on the same methodology and definitions, making them directly comparable. The initial development of the informality representation began with the most recent ILO-WIEGO data (2009 to 2013), appended the earlier years (2004—2008) and filled in missing values for 2009 to 2012 from the prior ILO-WIEGO dataset, and then did the same for the World Bank data, appending the years 1990—2004 and filling in any missing values from 2004—2011. Because the World Bank data is only presented as disaggregated by gender, we therefore took the intermediary step of computing a combined total series from the male and female percentages.
As we continue to update the data on informality, the ILOSTAT database at https://ilostat.ilo.org/topics/informality/ may be especially helpful. It has data on informal employment by sex in thousands of people, with scattered values for many countries (in late 2021 points were in the 2009-2020 period). The dataset differentiates informality for agriculture and non-agriculture sectors and for the total economy. For somewhat longer temporal coverage and with differentiation between informality in total and outside the formal sector (but without gender breakdown) a World Bank file in addition to those in the WDI system can be useful (at https://www.worldbank.org/en/research/brief/informal-economy-database).
7.2 Drivers of Informality
Building on conceptualization, measurement and data foundations, we developed four statistically-based structural components or statistical models in our forecasts of the informal economy: (1) a model of the size of the informal labor force; (2) a model of the distribution of informal labor residing either inside or outside of the informal sector; (3) a model of the informal economy expressed as a percent of official GDP; and (4) a model of the shadow economy expressed as a percent of official GDP. We use the output of the first model as a key but not sole driving variable for the subsequent three models.
Determinants of informality levels can be clustered into two general categories:
- Developmental drivers are a root cause of involuntary informality. They include low levels of human capital and low levels of economic opportunity in the formal economy. In developing countries with low levels of GDP per capita and higher levels of survivalist informality, developmental drivers may dominate. Even in more developed economies, where informality tends to exhibit different characteristics, a deeper developmental driver such as low levels of human capital may retain importance through its impact on the secondary drivers of informality.
- Secondary drivers are the push and pull factors that affect whether an actor will choose to enter, remain in, or opt-out of the formal economy. Many of these relate to governance character and quality, such as patterns of business regulation and taxation and levels of corruption. They can also be relatively immediate economic factors such unemployment levels and inflation rates.
A very large portion of the analysis and forecasting concerning informality has identified and used drivers in the secondary category. For instance, an OECD study (Andrews, Sánchez, and Johansson 2011) focused on property rights (emphasized earlier by de Soto 1986), the quality of governance, regulation, and fiscal and social policies (including social benefits). Given special attention by the OECD to higher-income member countries, that is not surprising. Also, however, analysis with MIMIC, often focused much more also on developing countries, has given considerable attention to levels of taxation, inflation, salaries, government (including regulation and consumption levels), and unemployment, although Elgin (2010: 13-16) also used GDP per capita and growth rate of it. Medina and Schneider (2018: 4) point out that the shadow economy can be defined as “all economic activities which are hidden from official authorities for monetary, regulatory and institutional reasons,” which leads them to focus on those drivers identified above as secondary. They point to early criticism of the MIMIC approach that used GDP per capita, and they do not.
Although shorter-term forecasting might well benefit from a nearly exclusive focus on secondary drivers, longer-term forecasting across a period during which lower-income countries with high levels of informality can expect substantial transformation of human capital and economic structure, requires significant attention to what we are calling developmental drivers.
The formulations of IFs for forecasting the shares of informality in labor and GDP draw upon seven explanatory variables as shown in Figure 7.1, each represented endogenously in the IFs model; they are designed to capture both the long-term relationship between human development and informality as well as the drivers that relate to the motivations and choices of firms and individuals and to the levers or policies of governments.
In the IFs model, developmental drivers are represented by years of educational attainment by adults (15 years and older), which serves as a proxy for overall levels of human capital. In terms of secondary drivers, three variables in the model tend to push enterprise from the formal to the informal sector, namely the nature of the business regulatory environment, the size of the tax burden, and the level of corruption. Two additional variables in IFs tend to pull informal activity toward formality, namely government to household transfers and spending on research and development.
Some literature of recent years identifies another development variable that logically and empirically has a close relationship with informality, namely the rate of urbanization. There has been rapid urbanization in developing countries since 1960, at which time approximately 80 percent of the population was rural. The rural percentages in low- and lower-middle- income countries fell by approximately 20 percentage points by 2020; in upper-middle-income countries the decline was 40 percentage points. That larger number was driven heavily by China with a decline of 44 percentage points, almost all after 1980.
For instance, Yuki (2007) explored the relationship between urbanization and the size of the informal economy and found that urbanization drives up informality unless it is accompanied by skill upgrading and especially industrialization with associated expansion of the formal economy. Ranis and Stewart (1999) found Thailand to be successful with this but the Philippines to fall short after the 1980s. Historical data in IFs suggest that while the manufacturing sector has grown substantially around the world since 1960, the tendency with respect to its share of economies has been most flat and somewhat decreasing (with growth primarily in the services sector). This has been true even in China, where the sector’s absolute growth has been driven by rapid GDP growth, not an increasing share of GDP. Hence Liu et al (2015) explored several alternative scenarios for the future with respect to the status of informal labor in China in the face of very rapid urbanization, with some pessimistic scenarios suggesting the difficulty of escaping a middle-income trap. This is also consistent with the findings of Elgin and Oyvat (2013) that there tends to be an inverted-U shaped curve for the share of informality within economies, driven upward in the period of especially rapid urbanization. And it is largely consistent with the relatively slow decline of the informal economy’s share of the total since 1960 across World Bank country income groupings, especially in low-income ones (data on the informal labor share across time are generally quite a bit less complete).
Statistical analysis with data in IFs shows that the share of the rural population in the total is significantly correlated with the share of informality (an R-squared of 0.34), while the relatively sparse data on informal labor share over time complicates broad analysis of the relationship between change in rural population share and informal labor share. The addition of rural population share as a development variable to analysis with educational attainment alone (or to analysis with GDP per capita alone), while showing relationship in the expected direction, does not add a statistically significant contribution or raise R-squared. Hence, in the formulations within IFs elaborated below, we have not to this point added urbanization.
And other models of informality, including variations of MIMIC and DGE models have not to our knowledge included the impact of urbanization. Elgin and Oyvat (2013) did find, however, that urbanization can add value to understanding differences across countries (and across time when longitudinal informality data are available) in datasets analyzed and built with attention to variables such as tax burden and institutional structure (e.g. that of Schneider et al. 2010 used in this project).
7.3 Forecasting Informality in Labor and GDP
The discussion of forecasting formulations begins with labor because of the clear importance of human capital in the development process and the causal contribution that informality of labor makes to informality of GDP. Following presentation of equations for forecasting the total share of the informal labor force, subsections turn to the division of that total into segments in the informal and formal economic sectors and to division by sex. Following sections move to the size of the informal GDP and the shadow economy.
The IFs model provides estimates of the overall size of the informal economy by calculating the shares of total labor and official GDP that are informal. The model begins by calculating the share of informal labor. A basic value of that percentage (LabInformal) is calculated as a function of four drivers: (1) Years of adult education (15+) (EDYRSAG15); (2) Government Business Regulation Index (GOVBUSREGIND); (3) Firm Tax Rates (FIRMTAXR); and (4) Government Transfers to Households for Welfare and Pensions as a percent of GDP (GOVHHTRN/GDP*100). The four driver terms are all from the previous model year (t-1), because in the recursive structure of IFs they are computed later in the sequence of variables.
Typically in IFs, major variable computations use the difference between the initial year’s computation of a value and a data value forwarded from the data preprocessor to compute a shift factor (basically a fixed effect) that is added to subsequent years and is converged toward zero over time. That was the initial approach used in the computation of labor informality when the model was built. It was found, however, that the initial year’s computation with estimated equations was often very far from the value loaded as data and that the approach using shift factors created poor forecast behavior. The formulation was then changed so that no shift factor is used and the movement across time from the data value of the base year is driven entirely by the changes in the driving variables relative to their values in the base year.
In the above equation, the basic values of the parameters are: labinformcoeffintercept=-12.613, labinformcoeffed= ,labinformcoeffbus = , labinformcoeffhhtrn= , labinformcoefftax= And in the above equation, education years are for the total population (sex=3) rather than males or females. Bohl, et al. (2015) elaborated the statistical basis for these parameters.
Changes in the level of informality often do not occur as rapidly as change in some of its drivers, so the computation above of LabInformal is smoothed over time with the smoothly changing historical value weighted 4 times as heavily as the current year’s calculation.
A multiplier on the informal share of labor (labinformshrm) exists for scenario analysis and is applied in a formulation that keeps the informal labor share between 1 and 85 percent.
It is very useful in our forecasting to know more about the makeup of informal labor. In particular, we want to know more about where that labor is employed and how it breaks down by sex. With respect to where it is employed, we use the categorization developed by the International Labor Organization and WIEGO, namely the portion of informal labor employed outside the informal sector (in the formal sector or in households) and the portion employed informally. We further divide each sub-section by sex.
The first step in computation is of the portion of informal labor employed inside the informal sector (LABINFORMPCNTINF), which varies inversely with the total share of labor that is informal (LABINFORMSHR). That is, as the informal share of total labor rises, a smaller portion of the total informal labor will be able to find positions in the formal sector (or as the informal share of total labor falls, the portion of the remaining informal labor employed in the formal sector will rise). This is computed for both sexes (s=Total) prior to a subsequent division by sex.
The values of the parameters currently are: infinformcoeffintercept=44.65; infinformcoefflabinf=- 0.417.
The percentage of the informal labor that is outside the informal sector (LABINFORMPCNTNONINF) is simply the residual.
The further division by sex of the informal labor by sector is done by using the initial patterns by sex (LABINFORMPCNTINFFemShare and LABINFORMPCNTNONINFFemShare). There are not enough data and conceptual foundations to establish a dynamic relationship for the share by sex. Thus in the equations below the sexual split of both the informal labor employed in the informal sector (LABINFORMPCNTINF) and the informal labor employed outside the informal sector (LABINFORMPCNTNOINF) is done using the proportions by sex in the model’s base year (t=1).
Similarly,
The IFs model uses three drivers to forecast informal GDP share: (1) the informal labor share (LABINFORMSHR); (2) the level of corruption (GOVCORRUPT); and (3) the society’s expenditure on research and development as a percentage of GDP (RANDEXP). Indirectly, the informal GDP share is, of course, also affected by the drivers of the informal labor share: (1) Years of adult education (15+) (EDYRSAG15); (2) Government Business Regulation Index (GOVBUSREGIND); (3) Firm Tax Rates (FIRMTAXR); and (4) Government Transfers to Households for Welfare and Pensions as a percent of GDP (GOVHHTRN/GDP*100). Earlier work with the model explored the impact on the GDP share of the portion of informal labor employed inside the informal economy (LABINFORMSEC, informal), but that is not in the formulation currently.
As in the computation of informal labor share, the forecast of informal GDP share as a percentage of official GDP (GDPINFORMSHR) involves two major steps. First, a basic value of that percentage (GDPInformal) is calculated as a function of the four drivers identified above. The driver terms are all from the previous model year (t-1), because in the recursive structure of IFs they are computed later in the sequence of variables.
In the above equation, the basic values of the parameters are: gdpinformcoeffintercept = 18.861, gdpinformcoefflabinf = 0.193, gdpinformcoeffcorrupt = -1.585, and gdpinformcoeffRanD = -2.608. The negative value on the corruption term is potentially misleading because in Transparency International's measure, higher values are more transparent and lower ones are more corrupt; the equation term increases GDPInformal as corruption increases.
The second step in the calculation of GDPINFORMSHR modifies that initial calculation of GDPInformal by converging a base year shift factor (GDPInformShrShift) to zero over a number of years specified by GDPInfConfYr and by applying an exogenous multiplier (gdpinformshrm). The base year shift factor adjustment is required to the calculation of GDPINFORMSHR because the initial (t=1) value of that variable from data will not be consistent with the calculation of it in the above function that generates GDPInformal. The adjustment or shift factor (GDPInformShrShift) is the difference in the first year between the value of GDPINFORMSHR and the calculated value from the driver function. It would be possible to maintain that additive shift factor as a constant over time, but because informal GDP shares generally decline with economic growth and changes in the associated secondary drivers used in the formulation, we converge that factor over time toward 0.0 or lack of adjustment. If the shift factor is greater than 0, we converge it in 70 years; otherwise in 200 years. The convergence process uses GDPInfConfYr, a variable that would often in IFs be specified externally but in this case is only computed and used internally The reason for the slower upward convergence is that, in general, the informal labor and GDP shares decrease with development, advance in GDP per capita and other associated drivers; upward movement would be very unusual.
7.3.5 Forecasting Size of the shadow economy
The shadow economy as a share of total is calculated using a formulation like that used for the informal share of the economy. Estimations from Schneider and Elgin were used to initialize the model in the base year (countries with missing data are initialized using a regression of the most recent year data against per capita GDP of countries). The regression model for shadow economy uses the same set of independent variables as did the model for the informal economy, i.e., informal labor share (LABINFORMSHR), corruption (GOVCORRUPT) and total R&D spending (RANDDEXP).
where r and t denote country/region and time, respectively
As discussed above for the informal economy, initial values and base year model calculations for the size of the shadow economy will typically differ. Shift factors are used to adjust computed values to those from data in the base year, and the shift factors converge to zero over time. There is also an exogenous multiplier term.
In the above equation, the basic values of the parameters are: gdpshadowcoeffintercept = 36.2814, gdpshadowcoefflabinf = 0.1019, gdpshadowcoeffcorrupt = -1.8849, and gdpshadowcoeffRanD = -2.9572. The negative value on the corruption term is potentially misleading because in Transparency International's measure, higher values are more transparent and lower ones are more corrupt; the equation term increases GDPSHADOWSHR as corruption increases.
For countries where the data on GDP share of shadow economy is greater than the informal labor share, indicating a somewhat counterintuitive situation in which the shadow sector seems to have a higher productivity per person than the formal economy, we accept those values in the model base year, but converge shadow GDP share to the informal labor shares over a period of 25 years.
7.4 Forward Linkages from the Informal Economy
The size of the informal economy is important in two forward linkages within the economic model itself; those were. The first is to economic growth and is elaborated in Section 2.7.4. The logic of the specification compares the share of economic informality in the GDP with an expected value and computes an adjustment factor for factor productivity. That adjustment factor can then raise or lower the stock variable of productivity (TEFF).
The second forward linkage similarly computes a separate adjustment factor (TaxInfAdjustmentFac) for government revenues and applies it to firm, household, indirect, and social security/welfare tax rates. Section 3.4.1.2 elaborates that linkage.
De Soto (1986) argued that the size of the informal economy, often driven in his analysis by inadequate provision by countries of property rights, contributed to terrorism levels, including his native Peru. No such forward impact is currently represented in IFs, but it could be considered as a driver of political instability.
8 Equality and Inequality: Distribution of Household Income
There are many ways to represent and forecast inequality. Almost all involve an aggregate index of income or consumption inequality, of which the Gini coefficient is the most common. In general terms, the representation of change in Gini across time and sociopolitical units involves either a statistical or a structural formulation. The statistical approaches typically drive the indices like Gini in relationships estimated by regression. The structural approaches compute the Gini (as shown subsequently in the Lorenz curve approach of Figure 8.1) via representation of the income or consumption shares of defined subpopulations. Not surprisingly, statistical analysis tends to pay close attention to the same drivers as does structural analysis. A good example of a statistical approach is Rao et al. (2019), which uses as drivers total factor productivity (TFP), educational attainment at different levels of education, and social public spending. The first two of those drivers have long been given attention in structural analysis of inequality. Acemoglu (2002) related inequality substantially to the balance of supply and demand for skilled and unskilled workers in the labor market. In general, demand for skilled labor rises with technical advance in the economy (and therefore also with GDP per capita). Supply of skilled labor rises with societal advance of education. With rapid advance in education, Acemoglu documented in the United States the decline of the “skill bias” or premium in wages for skilled workers in the 1970s as has occurred in other periods including early in the industrial revolution with the substitution for skilled artisans of capital-enhanced workers; he showed the reversal of that decline in subsequent decades, a pattern that raises inequality. Likewise, the statistical estimations of Rao et al. (2019) found a positive contribution to Gini (rising inequality) with TFP rise and a negative contribution with increase in educational attainment. They also found that progressive social policy (operationalized in terms of health and education spending as portions of public spending) pushed inequality down. The approach in IFs is heavily structural with similar drivers. It separately represents earnings and more comprehensive disposable income for skilled and unskilled households as a function of several forces, see the IFs documentation of economic production and social accounting (Sections 2 and 3) for more detail. Among factors that affecting its calculation of Gini: • The split of value added in each sector between capital and labor, recognizing that unskilled households are almost entirely dependent upon labor earnings, while skilled households also obtain a significant income boost to such earnings from return to capital. Model users can exogenously change the capital-labor split. • Beyond augmenting household disposal income from earnings with capital payments, IFs represents government transfer payments (net of taxes and social system contributions), which become much more substantial for unskilled households with higher incomes of countries. • The changing sectoral character of total labor demand with structural transformation of economies and the different skill requirements of sectors, including the lesser need for skilled labor in agriculture than in other sectors. Model users can also change the skill requirement balance in sectors. • Technical change will tend to raise demand for education and skills within as well as across sectors, a process that IFs represents with respect to the skill-level-demand for labor by sector using functions across GTAP data. • Changing educational attainment will shape the number of people in a society that can be characterized as skilled or unskilled. With respect to the division of labor into skilled and unskilled categories (see Sector 6 documentation of the labor model) IFs represents the educational attainment of working-age population in its education model. The model’s calculation of educational attainment is education-level specific, but the formulation for differentiating skilled and unskilled labor looks to average years of attainment across levels. That formulation also recognizes education credential requirement inflation across time. There are a variety of possible alternatives to the IFs population-category representation. Among these would be to move from a representation of Gini based simply on the differentiation between skilled and unskilled labor categories to other subsets of labor categories or to a specification of deciles of income distribution. The latter would require statistical representation across the deciles and is an approach elaborated in a project by Narayan et al. (2023) from the Pacific Northwest National Laboratory. And releases of data from GTAP now provide greater segmentation of labor force categories. Another more structural extension would take advantage of the modeling in IFs of informal labor to extend the model’s household category representation beyond simply skilled and unskilled. Agénor, Izquierdo, and Fofack (2003) looked to relationships among labor market segmentation (including size of informal economy), income inequality, and poverty (see also Agénor, Izquierdo, and Jensen 2007). They also recognized the importance of identifying government employment in the formal sector for low- and middle-income countries, suggesting a possible further structural enhancement. Although IFs does not represent income distribution by decile or quintile as a basis for representation of the Lorenz curve, it does use the representation of households in two education-based skill categories and the representation of disposal income in the same skill categories to create and use a simple Lorenz curve as a basis for calculating change in the Gini coefficient.
8.1 The Lorenz Curve and Gini Coefficient
The Lorenz curve is the most widely used method for representing inequality in earnings, income, or wealth (see Figure 8.1). It portrays the cumulative share of income (or any other quantity distributed across a population) held by increasingly well-to-do cumulative shares of population. The more equally distributed a factor is, the closer the Lorenz curve will be to the hypotenuse of the right-triangle, sometimes called the line of equality. The Gini coefficient is the “area of inequality” immediately below the hypotenuse (A) divided by the area of the triangle (A+B). Thus, larger Gini coefficients indicate greater inequality.
The Lorenz curve is “non-parametric” in the sense that it is an empirical distribution that can build on any representation of survey data on income or consumption for a society. While the Lorenz curve is useful conceptually and empirically to capture the dynamically evolving distribution of income or consumption in the Gini coefficient, for calculation of poverty numbers within a society it is more convenient to have an analytic or “parametric” summary representation of the distribution. Section 9 turns to analysis of poverty within IFs and discusses the use of the parametrically-based log-normal formulation for that analysis. That formulation is used with the Gini coefficient from the Lorenz curve as input. Here we will focus on the forecasting of the Lorenz curve in IFs and the calculation of the Gini coefficient from that forecasting.
Ideally, for the Lorenz curve’s foundation, the forecasting of segments of population from poorest to richest across the Lorenz curve should be tied to an elaboration of household types as is done with a Social Accounting Matrix (SAM). SAMs can distinguish multiple types of households with their changing demographic sizes (as a result, for instance, of rural-to-urban migration) and income structures (as a result of structural change in the economy, of changing patterns of government transfers, and many other factors). For the purposes of studying longer-term change in global poverty levels in IFs the SAM ideal is tarnished by two realities: (1) in spite of efforts via the UN’s System of National Accounts, there is no standard household classification system for SAMs. In fact, SAMs are very frequently used for single household categories in single-country analysis and (2) most models built around SAMs are used for rather short-term analysis and even more commonly for comparative static analysis (for example, comparison of income patterns in a society not open to agricultural imports to one that is, without much or any consideration of the dynamic path across time periods).
Nonetheless, the basic rooting of forecasts of a Lorenz curve and therefore of Gini in a SAM retains the tremendous advantage of tying those forecasts to changes in clearly policy-relevant interventions. And fortunately, the Global Trade and Analysis Project (GTAP) has long collected key information, such as share taken of value added, about two classes of households, those based respectively on skilled and unskilled labor, across the large number of countries/regions and economic sectors that the IFs project covers (see https://www.gtap.agecon.purdue.edu/default.asp).[6] Updating regularly to the most recent version, IFs has drawn heavily on the GTAP data in its own economic model structure and built the IFs SAM on the basis of the two household categories. The GTAP database has made it possible to develop forecasts of income by type of household as economies and therefore value added shares shift from agriculture to manufacturing and to services and as GDP per capita and therefore technology change. (See the documentation topics on household and firm income in Section 3.)
Although it is far from ideal to have only two categories of population (unskilled and skilled), it is possible to represent a Lorenz Curve showing what portion of income the unskilled (poorer) portion of the population obtains, specifying one point on the Lorenz curve that will fall below the diagonal (the line of equality). The unskilled and skilled portions together will receive all the income. Although simple, this Lorenz curve (actually two line segments), allows calculation of Gini.
Thus, for forecasting Gini we need only two things: the changing shares of income of the two groups and the changing sizes of the two groups. The social accounting matrix structure of IFs determines the household earnings by skill level and also the ultimate disposable income after transfers (HHINCDIS). It is the disposable income that we use in the computation of Gini. The labor market representation in IFs determines the share of labor that is skilled and unskilled. Other sections have provided documentation of both household income shares (Section 3.3.1.1) and the portions of labor that are skilled and unskilled (LABSUP) (Section 6.4). The latter, combined with total population, allow specification of the household population by skill level (HHPOP) in an equation that implicitly assumes the same household sizes for both skilled and unskilled labor.
8.2 Computing Domestic and Global Gini Coefficients
Given the income shares accruing to skilled and unskilled shares of the population and the sizes of those portions of the population, the domestic Gini index (GINIDOM) is computed from the simple Lorenz curve that those two incomes and population shares create, scaled to the empirically known base year Gini. The calculation in the Lorenz curve function GinDomiCalcFunc is modified by an additive scaling or shift parameter (GINIDomRI) so that the initial condition is preserved. A multiplier parameter (ginidomm) can change the calculation over time.
There is, however, an alternative and completely exogenous way of calculating Gini in IFs, if the parameter ginidomr has a value greater than 0. In that case, the value of Gini is simply the initial condition changed over time by ginidomr (again modified, if desired, by ginidomm).
Another option for model users is to keep GINIDOM at its initial year value. Setting ginidomcnstsw to some value other than its default of zero accomplishes that.
IFs also calculates two variations of a global Gini index to supplement the country-specific ones. The first is a Gini coefficient (GINI) that describes the distribution of GDP across country populations as the unit of analysis, computed in the GiniCalc function.
That measure does not take advantage of information about income distribution within countries. The second global Gini measure (GINIFULL) does account for income distributions both within and across countries as represented in GINIDOM. Moreover, it moves from GDP at market exchange rates to GDP at purchasing power parity (GDPP). That makes it more of a measure of effective global income distribution at the individual human level, rather than just across aggregate country populations. It uses the GiniFullNew function.
The code includes another function developed earlier, GiniFullCalc that computes the distribution of household income (HHINC) across countries treated equally rather than taking into account country populations. The function call is not now active and therefore no model variable reports its results.
Finally, the user interface of IFs uses the same Lorenz-curve approach to allow the user to calculate a generalized GINI for any model variable that is represented across all countries/regions of the model. It is found under Display/Specialized Displays for Issues/World Map, Lorenz Curve, Gini, Histogram. In that informative display one can, for instance, see a Lorenz Curve and Gini displaying how agricultural crop production is globally distributed relative to population in all years.
9 Poverty[7]
Closely related to its forecasting of economic development, income, and its distribution, the IFs project has long given attention to the forecasting of poverty and its reduction. It did so initially in the first volume of the project's Patterns of Potential Human Progress series, titled Reducing Global Poverty (Hughes et al. 2009). Subsequent Pardee Center work has updated and extended that work, often looking across alternative scenarios, including across the Shared Socioeconomic Pathways (Milante, Hughes, and Burt 2016; Moyer and Bohl 2018; Moyer and Hedden 2020) and, through a collaboration with the United Nations Development Programme, in the face of COVID (Hughes, Hanna, et al. 2021).
The ending of poverty in all its forms is the first target indicator of the Sustainable Development Goals is. Given its importance in the SDGs and as a fundamental measure of the human condition, many projects have developed capacity for forecasting the future of national and global poverty rates, mostly with a focus through the 2030 SDG target year, and a few to 2050. These include Edward and Summer (2013), Ravallion (2013), Kharas and Hamel (2020), Lakner et al. (2021), Mahler et al. (2020), Sumner, Hoy and Juarez (2020). Some analyses have looked across alternative scenarios (including Crespo Cuaresma et al. 2018). Forecasts in IFs run through 2100.
The World Development Report 1990 introduced the dollar-per-day international poverty line using purchasing power parity across national currencies (Ravallion et al., 1991). With inflation over time, the extreme poverty indicator variables that have received the most attention in recent years are the portion of national populations living on less than $1.90 ($2011) or $2.15 ($2017) and the World Bank defined a widely accepted target value for defining eradication of poverty and hunger as pushing them below 3 percent of population (Ravallion 2013). As progress has been made, more attention has been given also to the portion of populations living on less than $3.20 ($2011) or $3.65 ($2017) and $5.50 ($2011) or $6.85 ($2017). Through version 7.95 of IFs, GDP and other macroeconomic variables continued to be based in $2011, but that will be changing or have changed as data in $2017 become more complete. The IFs system includes variables for all of these poverty lines. In addition, the UN Entity for Gender Equity and the Empowerment of Women (UN Women) initiated a collaboration with the Pardee Center to analyze the extent of differences in poverty by sex and across age categories and to explore the potential for reduction of those differences. IFs further has a specialized display that allows the user to identify any other dollar value and includes other poverty related variables to be discussed below, including the poverty gap.
This documentation of the IFs approach first treats its representation of poverty rates in all countries or subunits thereof (percentage and numbers) and then moves to treatment of poverty by age and sex. In both cases it begins with the conceptual foundations and then turns to the specific forecasting formulations.
9.1 Poverty Rates and Numbers
Beginning with a focus on total poverty levels within a population, following subsections lay out the conceptualization of the portion of population in poverty and the drivers of change in that portion.
9.1.1 Conceptualization and drivers of poverty
Knowledge of two drivers allows quite accurate calculation of the portion of a population living at or below any specified poverty level: the average income (or household consumption) of the population and the distribution of that income. Once the rate of poverty is known, it requires only knowledge of a third driver, population size, to know also the number of people living below that poverty level. In dynamic societies there are, of course, a huge number of deeper or more distal drivers that affect these proximate drivers (literally anything that affects economic growth, the nature of income distribution, and the population size). Figure 9.1 shows this conceptual understanding of poverty, and indicates that the IFs system formalizes that understanding by calculating poverty from the three proximate drivers and also calculates those proximate drivers from the much larger forecasting system (the economic, population, and other models of IFs). The IFs system therefore makes available large numbers of intervention points for developing alternative scenarios around poverty futures.
Other parts of IFs documentation describe the determination of population and economic growth and of the calculation of the Gini coefficient (GINIDOM) as the key representation within IFs of income distribution. That documentation describes how the Gini coefficient is based on the Lorenz curve and how the Lorenz curve in IFs is tied to forecasting of the income shares of unskilled and skill households and the shares of population in those two household types (see Section 8).
The Lorenz curve of IFs with only two income categories is, however, a less than fully satisfactory form for representing the income distribution of the societies we forecast. It is both “non-parametric” in the sense that no simple analytical form can describe it for the purposes of our forecasting and it is crude in the representation of just the two income types. What we additionally want for poverty forecasting is an analytical form and one that can capture more smoothly the increasing income shares that richer portions of the population will have. (Ideally, we would also want a representation from which we can conveniently compute specific deciles or quintiles.)
The most widely used parametric representation in poverty analysis is the lognormal density. A density curve captures the percentage of the population that earns or consumes a given amount (unlike a distribution that captures the cumulative percentage of population that earns or consumes up to a given amount). Although income and consumption are not exactly distributed in a lognormal form for every country, it is a good approximation to observed empirical distributions for most (it will obviously not be such a good form for a country like post-Apartheid South Africa that has something closer to a binormal distribution). As Bourguignon (2004: 5) notes, a lognormal distribution is “a standard approximation of empirical distributions in the applied literature.”[8] A variable is lognormally distributed (see Figure 9.2) if the natural logarithm of that variable is normally distributed, as in the well-known “bell curve.”
One advantage of using a lognormal density to capture the distribution of income in a society is that it can be fully specified with only two parameters, average income and the standard deviation of it. More useful for our purposes, the Gini coefficient can be used in lieu of the standard deviation. See Appendix 2 of Hughes et al. (2009) for the explanation of that relationship and for much more information on the use of the lognormal distribution in IFs, including the calculations of poverty rates and poverty gaps, and the reconciliation of analysis using national accounts and survey data.
Figure 9.2 provides an illustration of how to obtain the poverty headcount from a lognormal density curve. For a specified poverty line—for example, the one corresponding to $1.90 a day—the area to the left of the line gives the poverty headcount ratio. The first vertical line in the figure shows that poverty line, and hatched lines show the area corresponding to the headcount ratio. The poverty headcount number is the headcount ratio times population.
Figure 9.3 similarly illustrates how changes in income distribution and the average level of per capita income can affect the poverty rate and therefore number. In this figure, the second vertical line from the left shows the income level for a given point in time, say Year 1, while the solid curve shows the income distribution. The third and dashed vertical line shows the income for a subsequent time, say Year 2, while the dashed curve shows an associated income distribution. The area of hatched, dashed lines to the left of the poverty line in the new distribution shows the new poverty headcount ratio. This area is smaller than the area under the Year 1 distribution, and the poverty headcount ratio has decreased. What happens to the poverty headcount number depends on the how the population has changed between the two years. If the population increases significantly, the headcount number can increase even if the headcount ratio decreases.
What is the evidence on poverty changes arising from the interaction of growth and distributional effects? There is evidence that growth tends to be “distribution neutral” on average; Ravallion and Chen (1997), Ravallion (2001), Dollar and Kraay (2002), find a close to zero correlation between changes in inequality and economic growth. There is also considerable evidence that the growth effect dominates efforts to reduce absolute poverty (World Bank 1990, 2000; Ravallion 1995; Ravallion and Chen 1997; Fields 2001, and Kraay 2004). World Bank (2001) and Ravallion (2004) suggest that the “elasticity” of the dollar-a-day poverty rate to growth is -2; an increase in the growth rate by 1% is associated with a decrease of 2% in the headcount index of poverty.
While there is much consensus that growth is good for poverty alleviation, voices of caution can be heard. The actual reduction in poverty is arguably lower than might be expected given recorded rates of economic growth. This has been termed “the paradox of persistent global poverty” (Cline 2004: 28; Dauda 2019 focused on Nigeria). Poverty in the 1990s declined by less than would have been predicted with a poverty-growth elasticity of around -2. Khan and Weiss (2006) warn that the elasticity of poverty to growth can vary widely—only -0.7 for the Philippines compared to -2.0 for Thailand—depending on the initial inequality and changes in inequality over time. Ravallion (2004) lists a few reasons to be cautious about the finding of distribution neutrality of growth: measurement error in changes in inequality, possible churning under the surface with winners and losers at all income levels, and possible increases in absolute income disparities. Moreover, a few countries and regions could experience poverty increases from distributional changes, even if on average there is neutrality.
In addition to uncertainties introduced by income inequality effects, the elasticity approach to anticipating poverty decline with income suffers from another problem. A given rate of economic growth will have a bigger impact on poverty headcount when the poor are clustered closely around the poverty line than when their incomes fall markedly below the line. In some countries this phenomenon might explain the weaker than expected response of poverty levels to growth in the face of only modest changes in overall inequality.
The lognormal approach, in interaction with separate representation of GDP growth and Gini and their drivers eliminated the need in IFs to use the elasticity approach upon which many studies have relied. In fact, a model using lognormal specifications can be used to calculate variable poverty elasticities across countries and time (and scenarios) in the face of very different patterns of relationship between GDP growth and change in Gini.
9.1.2 Lognormal Analysis of Change in Poverty
Given its advantages, the IFs approach to forecasting poverty uses the lognormal formulation, driven by average income (actually household consumption) and the Gini coefficient. One advantage of the approach is that the two drivers (average consumption and the log-normal function/distribution linked to Gini) allow the computation of poverty rates at any poverty level specified, which the specialized poverty display within the IFs system allows the user to do.
As indicated in the introduction to this Section 9, IFs focuses heavily on the poverty level consistent with the first of the Millennium Development Goals, namely eliminating extreme poverty, as well as poverty levels put forward by the World Bank in 2018 and associated with somewhat more moderate poverty.[9] In $2011 those levels have been $1.90, $3.20, and $5.50 per day and the IFs variables representing the number of people living below that level in each country are INCOMELT190LN, INCOMELT320LN, and INCOMELT550LN. In $2017 the levels are $2.15, $3.65, and $6.85 with variables named INCOMELT215LN, INCOMELT365LN, and INCOMELT685LN. The model also computes earlier or less-often discussed levels: INCOMELT110LN, INCOMELT125LN, INCOMELT200LN, and INCOMELT310LN. Within the flexible display of the IFs interface it is possible to see displays with the percentage of population below each of these levels. The computation of poverty numbers at each level is fundamentally identical, and we focus in explanation of the modeling on that for INCOMELT190LN.
One additional poverty line is not defined universally, but rather by country, and it (povnational) is read from World Bank data in the preprocessor. INCOMELTNPPLN is filled with the number of people who fall below those country lines. More generally, the World Bank also has largely through survey analysis built the most substantial and widely used database on poverty in its PovcalNet system (World Bank 2021), now replaced by the Poverty and Inequality Platform (PIP); IFs draws primarily on that data.
Although it is common to speak of poverty lines in terms of income, much of the survey data used to identify historical and contemporary levels and much of the conceptualization of poverty has focused on consumption (C), also recognizing the different purchasing power of dollar values of consumption around the world (PPPCONV). Therefore, IFs forecasts are driven by mean household consumption per capita (MeanConsumption or C divided by POP, adjusted by PPPCONV) and domestic Gini (GINDOM). Thus variables such as INCOMELT190LN are somewhat misnamed given the focus on consumption levels.
Both household consumption and Gini come to IFs from good data sources, but using them and the log normal distribution to compute poverty levels in the base year of the model inevitably produces values for percentage of the population that that differ somewhat from the survey data-based values of poverty. These values require reconciliation. It would be computationally possible to reconcile the initial data-based values of poverty with those calculated from initial values of household consumption, population, and Gini by using an additive or multiplicative “shift factor” as is often done in IFs when there is need for such reconciliation. A computationally and theoretically stronger approach is applying the reconciliation to household consumption values in the first year. Therefore, using a function PovRatInit that uses the log-normal function logic, IFs back calculates a mean consumption level (MeanBackCalc) in the first year from the data-based values of poverty rate (PortionPoor), the Gini value, and the log-normal distribution, using an inversion of the log-normal calculation system that computes the portion of the population that is poor in forecast years. The ratio of that back calculation from national survey data (NS) and the initial value of mean consumption from national accounts (NA) is a factor (e.g. NSNARat190Fac) that can be used to adjust the values of household consumption in future forecast years, producing values of poverty rates that change appropriate with household consumption and Gini.
The process in IFs for forecast years begins with the calculation of the lognormal standard deviation (LNStDev) from Gini and with the calculation of the mean consumption (MeanConsumption) from consumption per capita and a smoothed conversion factor from market exchange rates to purchasing power parity (SmPPPConv)―IFs endogenously computes changes in that PPP conversion factor over time (mostly converging toward 1 as national GDP per capita rises, see Section 2.10). These are the key drivers of the lognormal formulation. See Appendix 2 of Hughes et al. (2009) for a more formal and extended explanation of the entire poverty calculation system using the lognormal approach.
Given these driving inputs, IFs uses a two-step process for calculating the share of population below any given consumption level. The first step produces a log normal mean (LNMean) based on the mean consumption adjusted by the temporally invariant national accounts scaling factor computed in the first year (NSNARat190Fac) and the lognormal standard deviation. This calculation of the mean is a variant use of the log-normal function approach to calculation of poverty rate from mean consumption and Gini and draws on Function CalcNormalInverse. An exogenous parameter, nsnaratm can adjust the scaling factor over time.
Second, a specialized log-normal function computes the rate of poverty to be multiplied by the population to get the poverty numbers. That function, CalcLogNormalCDF calculates a cumulative distribution function where the logarithm of the variable is normally distributed. A hard-coded value in the equation below determines the daily consumption poverty level; other lines of code in IFs replace it with 3.20, 5.50, etc. to compute the portions of the population at various poverty levels. An exogenous parameter with a default value of 1.0 allows the user to change the poverty level in that calculation (incomepovlevm).
IFs is also able to compute the poverty gap at each level of poverty. The poverty gap (POVGAP) is defined as the mean shortfall from the poverty line, expressed as a percentage of the poverty line; the non-poor are considered to have zero shortfall. The measure helps identify the depth of poverty and is therefore a useful supplement to its incidence.
The base POVGAP variable is computed for the $1.90 per day extreme poverty line. The model similarly computes POVGAPxx for all other poverty lines identified with the INCOMELTExxxLN variables. It further computes POVGAPNPL for the measure of the poverty gap relative to nationally identified poverty lines.
Base year values for all POVGAP variables are initialized in the preprocessor from tables in IFsHistSeries.mdb carrying values from the World Bank’s data system. As with portions of the population in poverty, the IFs calculations of poverty gaps in the first year will differ from the World Bank data values. Thus, additive poverty gap shift factors (e.g., PovGap32Shift, PovGap55Shift) are computed in that first year, comparing the log-normal based values calculated in the model (CalcPovGap) with the data-based values.
In subsequent years the poverty gaps at all threshold levels are computed in the ComputePovGap function using the rate of poverty, population, domestic Gini, and the log-normal logic. In that function the additive shift factor is converged (in CalcShiftFactor) to 0 over 50 years (hard-coded) if it is positive and 200 years if it is negative and combined with a calculated poverty gap (CalcPovGap) that again draws on the portion of population in poverty, the Gini index, and the specified poverty level, all combined within a function that calculates the cumulative distribution function where the logarithm of the variable is normally distributed (CalcLogNormalCDF).
9.1.3 Cross-sectional analysis of poverty
Although the dominant approach to forecasting poverty in IFs uses the lognormal formulation, a simpler approach is also possible using a cross-sectional estimation of the relationship between poverty and GDP per capita at PPP. This simpler approach was developed for IFs before the lognormal one and applied to computing poverty at the 2005$ poverty lines of $1.00 and $2.00. The code and variable computations have been retained as a potentially useful second approach to estimate future poverty. In addition, in the preprocessor the cross-sectional formulation has been used to fill holes for countries without recent surveys in estimating initial poverty rates (even when forecasts then go on to use the logarithmic approach). Not surprisingly, the cross-sectionally estimated function uses the same proximate driving variables as the lognormal function, namely GDP per capita at PPP (GDPPCP) and domestic Gini (GINIDOM). A scaling factor computed the first year (IncomeLT1RI) assures that the value computed in the first year matches data when available; the factor is maintained in the calculation over time. The formulation for poverty at $2.00 per day (INCOMELT2CS) uses the same formulation as that below for $1.00 per day.
9.2 Poverty by Age and Sex
The number of people in poverty and the severity of it varies not only across countries but by age and sex. In a project with UN Women the IFs team added elaboration of its national poverty calculations to represent and forecast that variation, as a foundation for explorations of reductions especially in sexual differences. This unique extension of poverty forecasting, which divides total national poverty numbers into age and sex categories, requires attention in turn to conceptual and data foundations and to specific model formulations. For further elaboration, see Bohl and Irfan (2020), from which much the text for this section is drawn.
9.2.1 Conceptual and data foundations
Variables central to this study are the age-specific ratios of poverty rates by sex at each of the three $2011 poverty levels $(1.90, $3.20, $5.50), two $2017 levels ($3.65 and $6.85), and the nationally specific poverty line (POVGNDRATIO, POVGNDRATIO32, POVGNDRATIO55, POVGNDRATIO365, POVGNDRATIO685, and POVGNDRATIONPL). These build on and tie to the total national poverty levels with the same for thresholds (INCOMELT190LN, etc.).
As one foundation for initializing and forecasting the gender and age-specific variables, UN Women provided a database of age-sex poverty rates for 6 geographic regions and 30 individual countries within sub-Saharan Africa and South Asia.[10] The eight age-groups in this database are: 0-14, 15-24, 25-24, 35-39, 40-49, 50-54, 55-59, 60 and over. The IFs historical database currently includes national level poverty rates (population living on less than $1.90 and $3.10 per day) for all countries. Analysis within IFs allows forecasting in nine 5-year intervals plus 60 and over.
Among other data sources for national poverty rates and/or the age-sex disaggregation of poverty, we have used the World Bank’s PovCalNet now Poverty and Inequality Platform (PIP), the World Bank’s World Development Indicators, the World Poverty Clock (WPC) database, the Luxembourg Income Studies (LIS) database and the European-Union Statistics on Income and Living Conditions (EU-SILC) database. UN Women worked with LIS and EU-SILC to have their micro-data processed to age- and sex-specific poverty rates usable in the model.
The following graphic shows the poverty rate profile by age group across all countries for which we have data. In general, incidence of poverty is much higher among children (0-14) compared to poverty in other age-groups. At the global level, poverty rates tend to decline in older age categories.
Figure 9.5 compares age-group poverty rates by gender, showing the ratio of female-to-male poverty rates by age. It shows that the poverty burden for women is relatively higher among women in the peak child-bearing age group (25-34-year). A key motivation of the statistical analysis associated with this project has been to identify the drivers that underly this difference.
The pattern of the data-based age-specific gender differences clearly raises questions about the bases for them, especially with respect to (1) the age categories in which poverty appears lower for women than for men and (2) the “bouncing around” of direction in differences by sex in the age categories beginning with 40-49. Possibly, the lesser poverty of women than of men for the very oldest categories results in part from the tendency for women to out-live men in many societies and for that, especially in higher-income countries, to provide some inherited wealth-based income to the surviving women. Possibly also, it is an artifact of there being less population in those older age categories, giving prominence to the data-gathering challenges and associated uncertainties for them. On a global basis the 25-34 age category contains more than 1,196 million people, compared to about 920 million in the 60 and older category, which spreads across a much bigger age range. For developing countries, where most global poverty is , the ratio of the population in the 25-34 category to the 60 plus category is much higher. This gives us more confidence in the data for the lower age categories.
Further, the 25-34 category is that of peak child-bearing age, in which we might expect females to be further disadvantaged and want in policy interventions to give special attention. These reasons collectively lead us to focus in modeling and forecasting especially on that category and to translate changes in its poverty ratio to other categories proportionately (thereby actually reducing the advantages of women in the categories where they appear in the data to have lesser poverty).
The model as implemented will drive changes in female-male ratio of poverty rates, with development drivers generally reducing that ratio across the aggregate of all age categories within countries. The desired target for the ratio is, of course, equality.
In contrast to gender differences, there is reason to believe that age-based differences are likely to persist to some extent, albeit becoming less important as total poverty rates decline. Without earning power of their own, children are more susceptible to persistent poverty. On the other end of the age spectrum, however, in combination with increasing per capita levels of income and consumption with economic development, aging populations should be able to build wealth and income while governments also become more capable of supporting those who become older without having built wealth. Thus, we generally see less relative poverty of the elderly in more prosperous countries.
9.2.2 Modeling of poverty by age and sex
In addition, the UN Entity for Gender Equity and the Empowerment of Women (UN Women) initiated a collaboration with the Pardee Center to analyze the extent of differences in poverty by sex and across age categories and to explore the potential for reduction of those differences. This has resulted in the addition of several variables that represent poverty numbers (POVCOUNTxxx), rates (POVRATExxx), and gender ratios (POVGNDRATIOxxx) at various dollar per day poverty levels.
The conceptual and data foundations provide the basis for the modeling of poverty by age and sex, which is done for $1.90 in a function (IFsEcoPovAgeSex) called within the economic model (and similarly for other poverty levels). The steps are:
- Modeling change over time in the distribution of the rates and numbers of people in poverty (at each of the four primary poverty levels) across age categories. The initial calculations in the numbers by age are normalized to the country totals computed in advance of attention to age-sex patterns
- Representing changes over time in the female-male ratios within each age category. Because the formulations divide total numbers in each category into female and male poverty numbers, the sum across all 16 age-sex categories should automatically sum to the country totals, but a final normalization assures that it does.
9.2.2.1 Poverty by age
In the base year of model runs the initial age-group poverty ratios (iPovRateRatioToRefAG) are computed by dividing age-group poverty rates (POVRATE) with the total (All ages) poverty rate
where, the subscripts r, c, p and t represent country or region, age group or cohort, sex and time.
Across age groups, the high-income group ratios of poverty to national poverty serve as the target values (PovRateRatioToRefAG_Trgt) for age-group to total poverty ratio in the forecast years. The average per-capita income in the high-income group of countries to be used as a target (IncomeTrgt) is hard coded at 37.5 thousand PPP dollars (the value in 2015). At each time step, we first compute the portion of the path to the target covered (IncomeTrgtCov) by movement from the initial level of GDP per capita at PPP (GDPPCP)
Ratios (PovRateRatioToRefAG_Cur) of age-group poverty rates to total poverty are obtained by advancing these ratios towards their target by the same proportion as the advance of the income level to its target.
These ratios are multiplied with the total country poverty to obtain age-group poverty rates:
Poverty head counts (POVCOUNT) in each of the age groups are computed by multiplying age-group poverty rate (POVRATE) with age-group population (POPPOVAG), aggregated in a function (AggAgeDstFlex) from the much more disaggregated (cFull) age distribution (AgeDst) of the IFs population model.
Age-group poverty counts are normalized with the national poverty headcount (INCOMELT190LN).
The final values of the age-group poverty rates are computed from the normalized poverty count and population aggregated into the age categories.
9.2.2.2 Forecasting poverty rates by age and sex
Targets are important to all aspects of the modeling of poverty. The target in modeling of total national poverty is the eradication of it, recognizing that patterns of change will vary across identified poverty levels, recognizing that eradication realistically means movement of poverty rates at any such level below a somewhat arbitrary portion of the population such as 3 percent. In the modeling of poverty by age, the target pattern is that of high-income countries, recognizing that even in high-income countries there will likely remain somewhat more poverty among the very young and somewhat less poverty for those above 60 years of age.
In the modeling of sex ratios of poverty, the target is the elimination of poverty among females in excess of that for males. The conceptual and data discussion identified the ratio of female-to-male poverty rates in the 25-34 year-old age category as being the greatest across the eight age-groups used in this analysis, recognizing also its importance with respect to its typically large size among the categories and the importance of it with respect to child-bearing and early raising of them. The modeling logic therefore uses it as reference age-group and changes the ratio in other groups proportionately to change in it.
In the first year the model computes that age-category’s gender difference in rate (PovGndDiffRefAG) as a reference going forward.
where, RefAgGnd denotes the index of the reference age-group for the gender difference, i.e., 25 to 34-year-olds.
Going forward, the computed poverty gender difference in the reference age-group (PovGndDiffRefAGComp) is driven in our model by four variables – ratio of educational attainment (EDYRSAG15) between women and men, wage ratio between women and men (LABWAGESEXRAT), crude birth rate (CBR) and per person public welfare payment (GOVHHTRNWEL) to the households headed by an unskilled person (HHPOP). For literature on the theoretical and empirical basis for this equation see Appendix E (by Carole Green) in Bohl and Irfan (2020).
The analytical function above was obtained through a regression with a global cross-section of country data for the year 2017. Values for the dependent and the independent variables are obtained from historical databases collected from sources including the World Poverty Clock, UNDP, UNESCO and IMF. Missing base year values were filled in either from the most recent data sufficiently close to the base year or from imputation functions.
Regression residuals represent country shifts (PovGndDiffRefAGShift) in the model.
These country-shifts are added to the gender difference obtained from the analytical function. As the model runs, the initial country-specific shifts converge to zero across 50 years, using a linear interpolation routine (ConvergeOverTime).
From this gender difference forecast we subtract its initial value (PovGndDiffAG) to compute the percentage change in the reference group difference in each year (PcntChangeDiffRefAG).
Gender difference for the other age groups are obtained by adding to their initial year’s value the same percentage change in rate as accomplished by the reference age-group.
Once, the poverty gender difference is obtained for a specific age group, the both-sex, age-group poverty rate obtained earlier and the age-sex population aggregated into the eight categories (POPOVAG) are used to compute the age-group poverty rates by sex.
Female and male poverty headcounts by age-group are computed from poverty rates and age-sex population.
Female and male poverty headcounts and rates at the national level come from population weighted average of age-group poverty rates for each of the sexes.
To assure there are no differences between the total of national poverty and the values computed across the age and sec groups, some of the final steps above are done in a normalization routine (PovertyNormalizeGender).
9.2.2.3 Poverty shortfall
Poverty headcounts and rates do not say anything about the depth of poverty below the poverty line. An intensity measure called poverty gap is used for that purpose. The gap is the amount required to lift everyone to the poverty line. The shortfall is expressed in per capita terms by dividing the sum of shortfall for all poor (focusing again on INCOMELT190LN) with the national population (POP). This per capita poverty gap is then turned into an index (0-100) based on the poverty line (PPP $1.9 per day per capita).
We use the poverty gap index (POVGAP), computed at the national level, to calculate the poverty shortfalls (POVSHORT) in monetary terms for each of the age-sex groups. Each year, per poor shortfall (PerPoorShortFall) is first computed in thousand 2011 International Dollars.
The per poor shortfall is multiplied with the number of poor people in each of the age-sex group to compute poverty shortfall for each group (POVSHORT).
We also compute a gender difference in poverty shortfall (POVSHORTSEXDIFF) for each ()of the age-sex groups, distinguishing between those in which there is a positive shortfall for females relative to males and those where there is not (setting the value to 0 in those cases).
The variables above also allow computation in the model of the percentages of people 15 and older and 25 and older by gender who are living on the levels of poverty focused on in the model (POV15PCT, POV15PCT32, POV15PCTxxx). Further, IFs computes the variables shown in equations above across all of the IFs poverty threshold levels, including national poverty lines.
9.2.2.4 Parameters and scenario analysis
The model includes three switches that facilitate variations in analyses of poverty outcomes. Table 9.1 lists those.
| Parameter Name | Definition |
| povagesexgeneric | Poverty Switch for Generic Age-Sex Profile (1=On, 0=Off). A value of 0 (as in the base case) will use country specific age-sex poverty rates for model initialization. A value of 1 will use age-sex poverty rates from a generic profile for initializing all countries. |
| povagesexdynamic | Poverty Switch for Making Age-Sex Profile Dynamic (1=On, 0=Off). A value of 0 (as in the early version base case) will freeze NPL. A value of 1 will use dynamic models (full model base case) for age-sex poverty rates. |
| povagesexnormstatic | Poverty Switch for Normalizing Age-Sex Rates with a Constant Value (1=On, 0=Off). A value of 0 (as in the base case) will normalize age-sex poverty rates with the national poverty rate forecast. A value of 1 will normalize age-sex poverty rates using a constant national poverty rate, for example, the base year rate. |
Table 9.1. Parameters for scenarios relevant to poverty by age and sex. Source: David Bohl and Mohammod Irfan.
Beyond these parameters, users will be able to construct alterative scenarios by changing assumptions about the future of proximate and distal drivers of poverty and its distribution within a society.[11]
10 Acknowledgments
Thousands of IFs users over several decades have provided feedback for the improvement of the IFs system, one of the advantages of its having always been open source. To all of them, our thanks. Among those are individuals who have used IFs in research, policy analysis, training of professional users, and teaching (as well as students and interested individuals). Prominent among them making uncountable suggestions for its extension and improvement: Frederick S. Pardee, the founding sponsor of the Pardee Center, Jonathan D. Moyer, the second Director of the Pardee Center, and Keith Gehring, a teaching professor who has taught hundreds of students using IFs.
11 References
Abramowitz, M. 1986. Catching Up, Forging Ahead, and Falling Behind, Journal of Economic History 46: 385-406. doi.org/10.1017/S0022050700046209.
Acemoglu, Daron. 2002. “Technical Change, Inequality, and the Labor Market”, Journal of Economic Literature 40: 7-72.
Afman, E., and Maurel, M. 2010. “Diplomatic relations and trade reorientation in transition countries,” Chapter 10 in P. Van Bergeijk & S. Brakman (Eds.), The Gravity Model in International Trade: Advances and Applications (pp. 278-295). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511762109.010
Agénor,Pierre-Richard, Alejandro Izquierdo, and Hippolyte Fofack. 2003. “The Integrated Macroeconomic Model for Poverty Analysis: A Quantitative Macroeconomic Framework for the Analysis of Poverty Reduction Strategies,” Washington, D.C.: World Bank.
Agénor,Pierre-Richard, Alejandro Izquierdo, and Henning Tarp Jensen, eds. 2007. Adjustment Policies, Poverty and Unemployment: The IMMPA Framework. Malden, MA: Blackwell Publishing.
Aguiar, A., Narayanan, B., and McDougall, R. 201). An Overview of the GTAP 9 Data Base. Journal of Global Economic Analysis, 1(1), 181-208. doi:dx.doi.org/10.21642/JGEA.010103AF
Allen, R. G. D. 1968. Macro-Economic Theory: A Mathematical Treatment. New York: St. Martin's Press.
Almenar, Vicent, José Luis Sánchez, and Juan Sapena. 2020. “Measuring the shadow economy and its drivers: the case of peripheral EMU Countries,” Economic Research 33 (1): 2904-2918. https://doi.org/10.1080/1331677X.2019.1706601
Andrews, Dan, Aida Caldera Sánchez, and Asa Johansson 2011. Toward a Better Understanding of the Informal Economy, OECD Economics Department Working Papers No. 873.
Anderson, James E. 2010. “The Gravity Model,” Working Paper 16576. Cambridge, MA: National Bureau of Economic Research. https://www.nber.org/system/files/working_papers/w16576/w16576.pdf
Armington, Paul. S. 1969. “A Theory of Demand for Products Distinguished by Place of Production,” International Monetary Fund Staff Papers 16: 159-178. Available at https://www.jstor.org/stable/3866403
Barker, T.S. and A.W.A. Peterson, eds. 1987. The Cambridge Multisectoral Dynamic Model of the British Economy. Cambridge: Cambridge University Press.
Basu, Arnab K., Nancy H. Chau, Gary S. Fields, and Ravi Kanbur. 2016. “Job Creation in a Multi-Sector Labor Market Model for Developing Economies,” Forschunginstitut zur Zukunf der Arbeit Discussion Paper Series (IZA DP No. 9972).
Barnichon, Regis and Paula Garda. 2016. “Forecasting unemployment across countries: The ins and outs,” European Economic Review 84: 165-183. doi.org/10.1016/j.euroecorev.2015.10.006 Available at https://crei.cat/wp-content/uploads/users/working-papers/1-s2.0-S0014292115001555-main.pdf
Barro, Robert J. 1997. Determinants of Economic Growth: A Cross-Country Empirical Study. Cambridge, Mass: MIT Press.
Barro, Robert J. and Xavier Sala-i-Martin. 1999. Economic Growth. Cambridge, Mass: MIT Press.
Baumol, W. J. (1986) Productivity Growth, Convergence, and Welfare: What the Long-Run Data Show, American Economic Review 76 (5): 1072-1085. https://www.jstor.org/stable/1816469.
Birkmann, J. et al. (16 authors). 2013. “Scenarios for Vulnerability: Opportunities and Constraints in the Context of Climate Change and Disaster Risk,” Climatic Change. IFs used as primary tool. DOI 10.1007/s10584-013-0913-2.
Bohl, David K., Barry B. Hughes, Mohammod T. Irfan, Eli Margolese-Malin, and José Roberto Solórzano. 2015. Implementation of a Prospective Module about the Informal Economy in the IFs Model, in order to Adapt it to the Case of Peru. Denver: Frederick S. Pardee Center for International Futures, University of Denver. https://pardee.du.edu/sites/default/files/Bohl_2015_Ceplan.pdf and https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3764883
Bohl, David K. and Mohammod T. Irfan. 2020. “Forecasting the sex poverty gap: Model Scoping Document v05,” Frederick S. Pardee Center for International Futures and UN Women.
Bonnet, Florence, Joann Vanek and Martha Chen. 2019. Women and Men in the Informal Economy – A Statistical Brief. Manchester, UK: WIEGO
Bourguignon, Francois. 2004. “The Poverty-Growth-Inequality Triangle,” Working Paper No. 125, Indian Council for Research on International Economic Relations (CRIER). New Delhi. Available at https://www.econstor.eu/bitstream/10419/176147/1/icrier-wp-125.pdf
Bourmpoula, Evangelia, Roger Gomis and Steven Kapsos. 2017. ILO labour force estimates and projections: 1990-2030. (2017 Edition) Methodological Description. ILO, Geneva. http://www.ilo.org/ilostat-files/Documents/LFEP.pdf (Lastt access on July 12, 2018).
Bowlsby, D., Erica Chenoweth, Cullin Hendrix, and Jonathan D. Moyer. 2019. “The Future is a Moving Target: Predicting Political Instability,” British Journal of Political Science. January 20, 2019. doi: 10.1017/S0007123418000443.
Bremer, Stuart A. ed. 1987. The Globus Model: Computer Simulation of Worldwide Political Economic Development (Frankfurt and Boulder: Campus and Westview).
Brockmeier, Martina and Channing Arndt (presenter). 2002. Social Accounting Matrices. Powerpoint presentation on GTAP and SAMs (June 21). Found on the web.
Brzoza-Brzezina, Michal; Crespo Cuaresma, Jesus (2007). “Mr. Wicksell and the global economy: What drives real interest rates?,” Working Papers in Economics and Statistics, No. 2007-06, University of Innsbruck, Department of Public Finance, Innsbruck. https://www.econstor.eu/bitstream/10419/71917/1/742251934.pdf
Buehn, Andreas, and Friedrich Schneider. 2012. “Shadow Economies around the World: Novel Insights, Accepted Knowledge, and New Estimates.” International Tax and Public Finance 19(1): 139—171. doi:10.1007/s10797-011-9187
Bussolo, Maurizio, Mohamed Chemingui and David O’Connor. 2002. A Multi-Region Social Accounting Matrix (1995) and Regional Environmental General Equilibrium Model for India (REGEMI). Paris: OECD Development Centre (February). Available at www.oecd.org/dev/technics.
Cagan, Phillip (1958): "The demand for currency relative to the total money supply," Journal of Political Economy, 66:3, pp. 302-328.
Cantore, Nicola., and M. Cali. 2015. “The Impact of Temporary Migration on Source Countries,” International Migration Review. doi:10.1111/imre.12178.
Carrella, Ernesto. 2015. “Modeling Adaptive Economic Agents with PID Controllers,” PhD dissertation at George Mason University. Available at http://mars.gmu.edu/xmlui/bitstream/handle/1920/9862/Carrella_gmu_0883E_10909.pdf?sequence=1&isAllowed=y.
CEPLAN. 2016. Economía informal en Perú: situación actual y perspectivas. Recuperado de https://www.ceplan.gob.pe/documentos_/economia-informal-en-peru/
Chang, Sheldon S. L. 1961. Synthesis of Optimum Control Systems. New York, NY: McGraw Hill.
Chateau, Jean, Rob Dellink, Elisa Lanzi, and Bertrand Magné. 2012. “Long-Term Economic Growth and Environmental Pressure: Reference Scenario for Future Global Projections” Available at https://www.gtap.agecon.purdue.edu/resources/download/6003.pdf
Château, Jean., Rob Dellink and Elisa Lanzi. 2014. “An Overview of the OECD ENV-Linkages Model: Version 3”, OECD Environment Working Papers, No. 65, OECD Publishing. http://dx.doi.org/10.1787/5jz2qck2b2vd-en. Available at https://ledsgp.org/wp-content/uploads/2015/09/an-overview-of-the-OECD-ENV-Linkages-model.pdf
Chen, Martha Alter. 2012. “The Informal Economy: Definitions, Theories, and Policies.” WIEGO Working Paper no. 1. Women in Informal Employment Globalizing and Organizing (WIEGO), Cambridge, MA.
Chenery, Hollis, and Moises Syrquin. 1975. Patterns of Development, 1950-1970. London: Oxford University Press for the World Bank.
Chenery, Hollis. 1979. Structural Change and Development Policy. Baltimore: Johns Hopkins University Press.
Cline, William R. (2004). Trade Policy and Global Poverty. Washington DC: Center for Global Development and Institute for International Economics.
CPB Netherlands Bureau for Economic Policy Analysis. 1999. “WorldScan: The Core Version.” CPB Special Publication 20. CPB Netherlands Bureau for Economic Policy Analysis, The Hague the Netherlands. https://www.cpb.nl/sites/default/files/publicaties/download/worldscan-core-version.pdf.
Crespo Cuaresma, Jesús. 2017. Income Projections for Climate Change Research: A Framework Based on Human Capital Dynamics. Global Environmental Change 42(January): 226–236. DOI: 10.1016/j.gloenvcha.2015.02.012.
Crespo Cuaresma, Jesús et al. 2018. “Will the Sustainable Development Goals Be Fulfilled? Assessing Present and Future Global Poverty.” Palgrave Communications 4(1): 1–8.
Dauda, Rasaki Stephen. 2019. “The Paradox of Persistent Poverty Amid High Growth: The Case of Nigeria,” Chapter 11 in Paul Shaffer, Ravi Kanbur, and Richard Sandbrook, eds., Immiserizing Growth: When Growth Fails the Poor: 250-270. Oxford, England: Oxford University Press. DOI: 10.1093/oso/9780198832317.003.0011
De Benedictis, Luca and Daria Taglioni. 2011. “The Gravity Model in International Trade,” Chapter 4 in Luca De Benedictis and Luca Salvatici, ed., The Trade Impact of European Union Preferential Policies. Springer. Available at https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2384045.
De Soto, Hernando. 1986. The Other Path. New York: Basic Books. ISBN-10: 0465016103
Decreux, Yvan and Hugo Valin. 2007. MIRAGE, Updated Version of the Model for Trade Policy Analysis. CEPII (Centre d'Études Prospectives et d'Informations Internationales). http://www.cepii.fr/PDF_PUB/wp/2007/wp2007-15.pdf
Dellink, Rob, Jean Chateau, Elisa Lanzi, and Bertrand Magné. 2017. “Long-Term Economic Growth Projections in the Shared Socioeconomic Pathways.” Global Environmental Change 42(January): 200–214. DOI: 10.1016/j.gloenvcha.2015.06.004.
Dickson, Janet. R., Barry B. Hughes, and Mohammod T. Irfan. 2010. Advancing Global Education. Volume 2 in series on Patterns of Potential Human Progress. Boulder, CO USA and New Delhi: Paradigm Publishers and Oxford University Press-India. Review at http://www.tandfonline.com/doi/abs/10.1080/18146627.2010.490690. ISBN 9781594517563.
Dietz, Simon, and Nicolas Stern. 2015. “Endogenous Growth, Convexity of Damage and Climate Risk: How Nordhaus’ Framework Supports Deep Cuts in Carbon Emissions.” Economic Journal 125(583): 574–620. DOI: 10.1111/ecoj.12188.
Dimaranan, Betina V. and Robert A. McDougall, eds. 2002. Global Trade, Assistance, and Production: The GTAP 5 Data Base. Center for Global Trade Analysis, Purdue University. Available at http://www.gtap.agecon.purdue.edu/databases/v5/v5_doco.asp.
Dollar, David and Kraay Aart. (2002). "Growth is Good for the Poor". Journal of Economic Growth (7), 195-225.
Duchin, Faye. 1998. Structural Economics: Measuring Change in Technology, Lifestyles, and the Environment. Washington, D.C.: Island Press.
Edward, Peter, and Andy Sumner. 2013. The Future of Global Poverty in a Multi-Speed World: New Estimates of Scale and Location, 2010-2030. Washington D.C.: Center for Global Development. Working Paper. http://www.ssrn.com/abstract=2364153 (May 19, 2020).
Elgin, Ceyhun., M. Ayhan Kose, Franziska Ohnsorge, and Shu Yu. 2021. “Understanding Informality.” CERP Discussion Paper 16497, Centre for Economic Policy Research, London.
Elgin, Ceyhun, and O. Oztunali. 2012. “Shadow Economies around the World: Model Based Estimates.” Working Papers no. 2012/05. Department of Economics, Bogazici University, Istanbul.
Elgin, Ceyhún and Cem Oyvat. 2013. “Lurking in the cities: Urbanization and the informal economy,” Structural Change and Economic Dynamics 27: 36-47. https://doi.org/10.1016/j.strueco.2013.06.003
Erumban, A. A., and De Vries, K. (2016) Global Growth Projections for the Conference Board Global Economic Outlook 2017. Economics Program Working Paper Series EPWP #16-07. The Conference Board, New York, NY. https://www.conference-board.org/pdf_free/workingpapers/EPWP1607.pdf.
Fardoust, Shahrokh and Ashok Dhareshwar.2013. “Some Thoughts on Making Long-Term Forecasts for the World Economy.” World Bank: Policy Research Working Paper 6705. https://elibrary.worldbank.org/doi/abs/10.1596/1813-9450-6705 Also available on Academia.edu.
Faruqee, Hamid. 1995. “Long-Run Determinants of the Real Exchange Rate: A Stock-Flow Perspective,” IMF Staff Papers 42 (1): 80-107.
Feenstra, R. C., Inklaar R., and Timmer, M. P. (2015) The Next Generation of the Penn World Table, American Economic Review 105(10): 3150–3182. doi.org/10.1257/aer.20130954. Available for download at www.ggdc.net/pwt.
Fields, Gary S. 2005. “A Guide to Multisector Labor Market Models,” World Bank Human Development Network Social Protection Unit Discussion Paper.
Friedman, Milton. 1957. A Theory of Consumption. Princeton: Princeton University Press. ISBN 978-0-691-04182-7
Globerman, Steven. 2000 (May). Linkages Between Technological Change and Productivity Growth. Industry Canada Research Publications Program: Occasional Paper 23.
Gordon, Theodore, Barry B. Hughes, José R. Solórzano, and Marc Stelzner. 2011. “Producing State of the Future Indexes Using the International Futures Model,” Technological Forecasting and Social Change 78 (1): 75-89. https://doi.org/10.1016/j.techfore.2010.10.007 (2011).
Green, Russell and Tom Torgerson. 2007. “Are High Foreign Exchange Reserves in Emerging Markets a Blessing or a Burden?” United States Department of the Treasury, Office of International Affairs, Occasional Paper No. 6 (March). Available at http://www.treas.gov/offices/international-affairs/occasional-paper-series/docs/reserves.pdf.
Griffith, Rachel, Stephen Redding, and John Van Reenen. 2000. Mapping the Two Faces of R&D: Productivity Growth in a Panel of OECD Industries. Institute for Fiscal Studies (January).
Gyomai, György. 2012. “Summary of the OECD Survey on Measuring the Non-Observed Economy.” Working Party on National Accounts. OECD, Paris.
Gyomai, György, and Peter van de Ven. 2014. “The Non-Observed Economy in the System of National Accounts.” Working Party on National Accounts. OECD, Paris.
Hall, Robert E. 1978. “Stochastic Implications of the Life Cycle-Permanent Income Hypothesis: Theory and Evidence,” Journal of Political Economy 86 (6): 971-986. http://www.bu.edu/econ/files/2011/01/hall.pdf.
Harris, John R. and Michael P. Todaro. 1970. “Migration, Unemployment and Development: A Two-Sector Analysis,” American Economic Review 60 (1): 126-142.
Hawkins, Raymond J., Jeffrey K. Speakes, and Dan E. Hamilton. 2014. “Monetary policy and PID Control,” Journal of Economic Interaction and Coordination DOI 10.1007/s11403-014-0127-3 https://www.imfs-frankfurt.de/fileadmin/user_upload/Events_2018/MMCI_Conference/Papers/09-Raymond_Hawkins-Monetary_Policy_and_PID_Control.pdf
Hamidian, Hamideh and Ali Akbar Jalali. 2011. “Calculation of PID Controller Parameters for Unstable First Order Time Delay Systems,” International Journal of Scientific and Engineering Research 2 (3): 6 pages. Available at https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.301.7319&rep=rep1&type=pdf
Hanna, T., Bohl, D. K., & Moyer, J. D. (2021). Assessing the Impact of War in Yemen: Pathways for Recovery. United Nations Development Programme and Frederick S. Pardee Center for International Futures.https://korbel.du.edu/sites/default/files/2021-12/UNDP-Yemen_ImpactofWar_WEB.pdf
Head, Keith and Thierry Mayer, 2014. "Gravity Equations: Workhorse,Toolkit, and Cookbook," Handbook of International Economics, in: Gopinath, G. & Helpman, . & Rogoff, K. (ed.), Handbook of International Economics, edition 1, volume 4, chapter 0, pages 131-195, Elsevier.
Hillebrand, Evan E. 2008. “The Global Distribution of Income in 2050,” World Development 36 (5): 727–740.
Hillebrand, Evan. E. 2010. “Deglobalization Scenarios: Who Wins? Who Loses?” Global Economy Journal 36 (5). doi:10.2202/1524-5861.1611.
Hughes, Barry B. 1986. ”The First Two Oil Shocks: Policy Response and Effectiveness,” Policy Studies Review 5 (4): 722-741. Selected by the Policy Studies Organization for the Fourth Annual Jeffrey Pressman Award as the year’s outstanding article published in Policy Studies Review. https://web-p-ebscohost-com.du.idm.oclc.org/ehost/pdfviewer/pdfviewer?vid=1&sid=712d2fa9-3045-4e17-b38a-a010a69f62d6%40redis.
Hughes, Barry B. 1987. "Domestic Economic Processes," in Stuart A. Bremer, ed., The Globus Model: Computer Simulation of Worldwide Political Economic Development (Frankfurt and Boulder: Campus and Westview), pp. 39-158.
Hughes, Barry, B. 1997. “Rough Road Ahead: Global Transformations in the 21st Century,” Futures Research Quarterly13(2): 83-107. https://pardee.du.edu/sites/default/files/RoughRoadAhead.pdf.
Hughes, Barry. B. 1999. “The International Futures (IFs) Modeling Project,” Simulation and Gaming 30 (3): 304-326.
Hughes, Barry B. 2001a “Choices in the Face of Uncertainty: The International Futures (IFs) Model,” Futures 33: 55-62 https://doi.org/10.1016/S0016-3287(00)00053-7.
Hughes, Barry B. 2001b. “Global Social Transformation: The Sweet Spot, the Steady Slog, and the Systemic Shift,” Economic Development and Cultural Change 49, No. 2 (January): 423-458.
Hughes, Barry B. 2005. "Forecasting Productivity and Growth with International Futures (IFs) Part 1: The Productivity Formulation," Pardee IFs Working Paper 2005.05.01, available at http://pardee.du.edu/sites/default/files/WP_2005_05_Productivity_Growth_IFs_Part1_0.pdf.
Hughes, B. B. 2016. “International Futures (IFs) and integrated, long-term forecasting of global transformations,” Futures, 81, 98–118 https://doi.org/10.1016/j.futures.2015.07.007.
Hughes, Barry B. 2019. International Futures: Building and Using Global Models. London: Elsevier Academic Press. ISBN: 9780128042717.
Hughes, Barry B., David Bohl, Mohammod T. Irfan, Eli Margolese-Malin, and José R. Solórzano. 2017. “ICT/Cyber Benefits and Costs: Reconciling Competing Perspectives on the Current and Future Balance,” Technological Forecasting and Social Change 115: 117-130. http://dx.doi.org/10.1016/j.techfore.2016.09.027 and open access at https://authors.elsevier.com/sd/article/S0040-1625(16)30356-0.
Hughes, Barry B., Taylor Hanna, Kaylin McNeil, David K. Bohl, and Jonathan D. Moyer. 2021. "Pursuing the Sustainable Development Goals in a World Reshaped by COVID-19: Foundational Research Report,” Denver, Co and New York, NY: Frederick S. Pardee Center for International Futures and the United Nations Development Programme. Available at https://sdgintegration.undp.org/sites/default/files/Foundational_research_report.pdf
Hughes, Barry.B. and Hillebrand, Evan.E. 2006. Exploring and Shaping International Futures. Boulder, CO: Paradigm Publishers.
Hughes, Barry B. and Anwar Hossain. 2003. "Long-Term Socio-Economic Modeling: With Universal, Globally-Integrated Social Accounting Matrices (SAMs) in a General Equilibrium Model Structure." IFs Project Living Document, University of Denver.
Hughes, Barry B. with Mohammod T. Irfan. 2006. "The Data Preprocessor of International Futures (IFs).” IFs Project Living Document, University of Denver.
Hughes, Barry B. and Mohammod T. Irfan. 2007. “Assessing Strategies for Reducing Poverty,” International Studies Review 9 (4): 690-710. https://www.jstor.org/stable/4621868.
Hughes, Barry B. with Mohammod T. Irfan. 2013 (v. 2013.07.12). "The Data Pre-Processor of International Futures (IFs).” IFs Project Living Document, University of Denver.
Hughes, Barry B. with Mohammod T. Irfan. 2018 (v. 14). "IFs Labor Model Documentation.” IFs Project Living Document, University of Denver.
Hughes, Barry B. and Peter D. Johnston. 2005. Sustainable Futures: Building Policy Options into A Scenario for Development in a Global Knowledge Society. Futures 37(8): 813-831. https://doi.org/10.1016/j.futures.2005.01.017.
Hughes, Barry B., Mohammod T. Irfan, Haider Khan, Krishna Kumar, Dale S. Rothman, and José Roberto Solórzano. 2009. Reducing Global Poverty. vol. 1, Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Hughes, Barry B., Mohammod T. Irfan, Jonathan D. Moyer, Dale S. Rothman, and José R. Solórzano. 2011. “Forecasting the Impacts of Environmental Constraints on Human Development,” Sustainability 4 (5): 958-994. With Appendix on the model. doi:10.3390/su4050958. Earlier version was Research Paper 2011/08 for the United Nations Human Development Report 2011.
Hughes, Barry B., Mohammod T. Irfan, José R. Solórzano, Vivian Yang, and Jonathan D. Moyer. 2020. “Estimating Current Values of Sustainable Development Goal Indicators Using an Integrated Assessment Modeling Platform: “Nowcasting” with International Futures,” Statistical Journal of the IAOS, vol. Pre-press, pp 1-15. DOI: 10.3233/SJI-200715
Hughes, Barry B., Devin K. Joshi, Jonathan D. Moyer, Timothy D. Sisk, and José R. Solórzano. 2014. Strengthening Governance Globally. Vol. 5 of the Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Hughes, Barry. B., Randall Kuhn, Eli S. Margolese-Malin, Dale S. Rothman, and José R. Solórzano. 2015. “Opportunities and Challenges of a World with Negligible Senescence,” Technological Forecasting and Social Change 99: 77-91. http://dx.doi.org/10.1016/j.techfore.2015.06.031.
Hughes, Barry B., Randall Kuhn, Cecilia M. Peterson, Dale S. Rothman, José R. Solórzano 2011. Improving Global Health. Volume 3 in series on Patterns of Potential Human Progress. Boulder, CO USA and New Delhi: Paradigm Publishers and Oxford University Press-India. ISBN 9781594518973.
Hughes, Barry B., Randall Kuhn, Cecilia M. Peterson, Dale S. Rothman, José R. Solórzano, Colin D. Mathers, and Janet R. Dickson. 2011. “Projections of global health outcomes from 2005 to 2060 using the International Futures integrated forecasting model,” Bulletin of the World Health Organization. 89 (7): 469-544.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3127264/pdf/BLT.10.083766.pdf.
Hughes, Barry B., and Kanishka Narayan. 2021. “Enhancing Integrated Analysis of National and Global Goal Pursuit by Endogenizing Economic Productivity” PLOS One 16(2); e0246797 Pre-press, 24 pages. DOI: 10.1371/journal.pone.0246797
Hughes, Barry B., José R. Solórzano and Dale S. Rothman 2023 “IFs Energy Model Documentation” in Pardee Center file Energy Documentation v9.doc.
Hussmanns, Ralf., Farhad Mehran, and Vijaya Varmā. 1990. Surveys of economically active population, employment,unemployment, and underemployment: An ILO manual on concepts and methods. International Labour Organization, Geneva.
Instituto Nacional de Estadistica e Informatica (INEI). 2014. “Satellite Account of the Informal Economy: Production and Informal Employment in Peru 2007—2012.” Working Document 7/3/2014. INEI, Lima, Perú.
International Labour Organization. n.d. ILOSTAT. http://www.ilo.org/ilostat Access on 07/15/2018
International Monetary Fund (IMF). 2009. Balance of Payments and International Investment Position Manual. Sixth edition. Washington, D.C.: IMF https://doi.org/10.5089/9781589068124.069
International Labour Organization (ILO). 2013. Measuring Informality: A Statistical Manual on the Informal Sector and Informal Employment. Geneva: International Labour Office.
https://www.wiego.org/sites/default/files/publications/files/Women%20and%20Men%20in%20the%20Informal%20Economy%203rd%20Edition%202018.pdf
International Labour Organization (ILO). 2018. Women and men in the informal economy: a statistical picture (third edition). Geneva: ILO.
International Labour Organization (ILO). 2022a (January). ILO modelled estimates: Methodological overview. ILO Department of Statistics. https://www.ilo.org/ilostat-files/Documents/TEM.pdf
International Labour Organization (ILO). 2022b. World Employment and Social Outlook Trends 2022. Geneva: ILO. https://www.ilo.org/wcmsp5/groups/public/---dgreports/---dcomm/---publ/documents/publication/wcms_834081.pdf
International Monetary Fund (IMF). 2021. Measuring the Informal Economy. IMF Policy Paper. https://www.imf.org/en/Publications/Policy-Papers/Issues/2021/02/02/Measuring-the-Informal-Economy-50057
Jansen, Karel and Rob Vos, eds. 1997. External Finance and Adjustment: Failure and Success in the Developing World. London: Macmillan Press Ltd.
Johansson, Åsa, et al. 2012. “Looking to 2060: Long-term global growth prospects.” Paris: OECD. Available at https://www.oecd.org/economy/outlook/2060%20policy%20paper%20FINAL.pdf
Johnson, P. and Papageorgiou C. (2020) What Remains of Cross-Country Convergence? Journal of Economic Literature 58 (1) (March) DOI: 10.1257/jel.20181207.
Joshi, Devin. K., Barry B. Hughes, and Timothy D. Sisk. “Improving Governance for the post-2015 Sustainable Development Goals: Scenario Forecasting for the Next 50 Years,” World Development 70: 286-302. http://dx.doi.org/10.1016/j.worlddev.2015.01.013.
Kabandula, Abigail, David K. Bohl, Jonathan D. Moyer, Taylor Hanna, Barry B. Hughes, Yutang Xiong, Collin J. Meisel. 2020. Conditions for Success in the implementation of the African Continental Free Trade Agreement: Reference Report. University of Denver: Frederick S. Pardee Center for International Futures. https://korbel.du.edu/pardee/resources/conditions-success-implementation-african-continental-free-trade-agreement
Kehoe, Timothy J. 1996. Social Accounting Matrices and Applied General Equilibrium Models. Federal Reserve Bank of Minneapolis, Working Paper 563.
Khan, Haider A. 1998. Technology, Development and Democracy. Northhampton, Mass: Edward Elgar Publishing Co.
Khan, Haider and John Weiss (Eds.). (2006). Poverty Strategies in Asia: Growth Plus Approach. Cheltenham, UK: Edward Elgar.
Kharas, Homi, and Kristofer Hamel. 2020. “Turning Back the Poverty Clock: How Will COVID-19 Impact the World’s Poorest People?” Brookings.
Kornai, J. 1971. Anti-Equilibrium. Amsterdam: North Holland.
Kraay, Aart. (2004). "When is Growth Pro-poor? Cross-Country Evidence". WP/04/47: IMF Working Paper: New York, NY. http://www.imf.org/external/pubs/ft/wp/2004/wp0447.pdf.
Kuhn, Randall, Dale Rothman., Sara Turner, José Solórzano, and Barry B. Hughes. 2016. “Beyond Attributable Burden: Estimating the avoidable burden of disease associated with household air pollution.” PLoS One11(3):e0149669.** doi: 10.1371/journal.pone.0149669. eCollection 2016. https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0149669&type=printable.
Kuznets, Simon. 1959. “On Comparative Study of Economic Structure and Growth of Nations.” In The Comparative Study of Economic Growth and Structure. New York: NBER, pp. 162-176.
———. 1966. Modern Economic Growth: Rate, Structure, and Spread. New Haven: Yale University Press.
Lane, Philip R. 2019. “Determinants of the real interest rate,” Remarks by the member of the Executive Board of the European Central Bank at the Annual Investee and Business Leader’s Dinner. Available through the Bank at https://www.ecb.europa.eu/press/key/date/2019/html/ecb.sp191128_1~de8e7283e6.en.html
Lee, Ronald, Andrew Mason, and Timothy Miller. 1998 "Life Cycle Saving and the Demographic Transition in East Asia." Working Paper for Population and Economic Change in East Asia a supplement to Volume 26 of Population and Development Review.
Lee, Ronald D. and Andrew Mason, eds. 2011. Population Aging and the Generational Economy: A Global Perspective.Cheltenham, UK: Edward Elgar. Available at http://idl-bnc.idrc.ca/dspace/bitstream/10625/47092/1/133467.pdf.
Leontief, Wassily. 1951. The Structure of the American Economy, 1919–1939. 2d ed. White Plains, NY: International Arts and Sciences Press.
Lewer, Joshua J. and Hendrik Van den Berg. 2008. “A Gravity Model of Immigration,” Economics Letters 99:1 (April): 164-167. doi 10.1016/j.econlet.2007.06.019 Available at https://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1023&context=managementfacpub .
Liu, Dehai, Hongyi Li, Weiguo Wang, and Chuang Zhou. “Scenario forecast model of long term trends in rural labor transfer based on evolutionary games,” Journal of Evolutionary Economics 25 (3): 649-670. DOI 10.1007/s00191-015-0393-9
Lofgren, Hans, Sherman Robinson, Rebecca Lee Harris. 2002. A Standard Computable General Equilibrium (CGE) Model in GAMS. Washington, D.C.: International Food Policy Research Institute (IFRPI). Available at https://www.ifpri.org/publication/standard-computable-general-equilibrium-cge-model-gams-0
Loichinger Elke. 2015. “Labor force projections up to 2053 for 26 EU countries, by age, sex, and highest level of educational attainment”. Demographic Research 32 (15): 443−486. Available at https://www.demographic-research.org/volumes/vol32/15/32-15.pdf
Lutz, Wolfgang, and Samir KC. 2014. “The Rise of Global Human Capital and the End of World Population Growth.” In Wolfgang Lutz, William P. Butz, and Samir KC, eds., World Population and Human Capital in the Twenty-First Century. Oxford, UK: Oxford University Press, 519–562.
Macdonald, Ryan. 2010. “Real Gross Domestic Income, Relative Prices, and Economic Performance across the OECD,” Review of Income and Wealth 56 (3): 498-518. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.655.6455&rep=rep1&type=pdf
Mahler, Daniel Gerszon, Christoph Lakner, Andres Castaneda Aguilar, and Haoyu Wu. 2020. “The Impact of COVID-19 (Coronavirus) on Global Poverty: Why Sub-Saharan Africa Might Be the Region Hardest Hit.” The impact of COVID-19 (Coronavirus) on global poverty: Why Sub-Saharan Africa might be the region hardest hit. https://blogs.worldbank.org/opendata/impact-covid-19-coronavirus-global-poverty-why-sub-saharan-africa-might-be-region-hardest (May 18, 2020).
McMahon, Walter W. 1997. Education and Development: Measuring the Social Benefits. Oxford: Oxford University Press.
Meadows, Donella H. 2008 (edited by Diana Wright after her death). Thinking in Systems: A Primer. London: Earthscan and Sterling, Va: Chelsea Green Publishing. Available at http://www.uvm.edu/~lpolya/ENVS%20295/Readings/Thinking%20in%20Systems,%20pages%2035-58.pdf
Medina, Leandro and Friedrich Schneider. 2018. “Shadow Economies Around the World: What Did we Learn Over the Last 20 Years? IMF Working Paper 18/17.
Mesarovic, Mihajlo D., and Eduard Pestel, eds. 1974a. Multilevel Computer Model of World Development System. Vol 1–6. Extracts from Symposium Proceedings, Laxenburg, Austria, April 29–May 3, 1974. Laxenburg, Austria: International Institute for Applied Systems Analysis.
Mesarovic, Mihajlo D., and Eduard Pestel. 1974b. Mankind at the Turning Point. New York: E.P.Dutton & Co.
Milante, Gary, Barry B. Hughes, and Alison Burt. 2016. Poverty Eradication in Fragile Places: Prospects for Harvesting the Highest Hanging Fruit by 2030. Stability: International Journal of Security and Development 5 (1): 7; 1-24. http://dx.doi.org/10.5334/sta.435 Earlier version was World Bank Policy Research Working Paper 7002. Washington D.C.: World Bank. Available at http://documents.worldbank.org/curated/en/2014/08/20040315/eradicating-poverty-fragile-states-prospects-reaching-high-hanging-fruit-2030. (2016).
Mishkin, Eli, and Ludwig Braun, eds. 1961. Adaptive Control Systems. New York, NY: McGraw Hill.
Modigliani, Franco. 1976. “Life-cycle, individual thrift, and the wealth of nations,” American Economic Review, 76(3), 297–313.
Moyer, Jonathan D., and David K. Bohl. 2019. “Alternative Pathways to Human Development: Assessing Trade-Offs and Synergies in Achieving the Sustainable Development Goals.” Futures. http://www.sciencedirect.com/science/article/pii/S0016328718302040.
Moyer, J. D., Bohl, D., Hanna, T., Mapes, B. R., & Rafa, M. (2019). Assessing the Impact of War on Development in Yemen. Frederick S. Pardee Center for International Futures and Josef Korbel School of International Studies and United Nations Development Programme. https://yemen.un.org/sites/default/files/2019-09/Assessing%20the%20Impact%20of%20War%20on%20Development%20in%20Yemen.pdf
Moyer, J. D., Hanna, T., Bohl, D. K., & Mapes, B. R. (2019). Assessing the Impact of War in Yemen on Achieving the Sustainable Development Goals [Invited Research Paper]. Report for UNDP by the Frederick S. Pardee Center for International Futures, Josef Korbel School of International Studies. https://reliefweb.int/sites/reliefweb.int/files/resources/UNDP-YEM%20War%20Impact%20on%20SDGs_compressed.pdf
Moyer, Jonathan D. and Barry B. Hughes. 2012. “ICTs: Do they contribute to climate change or sustainable development?” Technological Forecasting and Social Change. 2012. doi:10.1016/j.techfore.2011.12.005.
Moyer, Jonathan D., Collin J. Meisel, Austin S. Matthews, David K. Bohl, and Matthew J. Burrows. 2021. China-US Competition: Measuring Global Influence. Atlantic Council and Frederick S. Pardee Center for International Futures. ISBN-13: 978-1-61977-173-4 https://www.atlanticcouncil.org/wp-content/uploads/2021/06/China-US-Competition-Report-2021.pdf
Moyer, Jonathan D., and Steve Hedden. 2020. “Are We on the Right Path to Achieve the Sustainable Development Goals?” World Development 127: 104749.
Moyer, Jonathan D., Tim Sweijs, Mathew J. Burrows, and Hugo Van Manen. 2018. Power and Influence in a Globalized World. Washington, D.C.: The Atlantic Council with the Frederick S. Pardee Center for International Futures. https://defaeroreport.com/2018/02/26/atlantic-council-power-influence-globalized-world/
Moyer, Jonathan. D., Willem Verhagen, Brendan Mapes, David K. Bohl, Yutang Xiong, Vivian Yang, K. McNeill, José R. Solórzano, Mohammod T. Irfan, C. Carter, and Barry B. Hughes. 2022. How many people is the COVID-19 pandemic pushing into poverty? A long-term forecast to 2050 with alternative scenarios. PLOS ONE 17 (7): e0270846. https://doi.org/10.1371/journal.pone.0270846.
Muller,Ulrich K., James H. Stock, and Mark W. Watson. 2022. “An Econometric Model of International Growth Dynamics for Long-Horizon Forecasting,” The Review of Economics and Statistics 104 (5): 857-876. https://doi.org/10.1162/rest_a_00997
Narayan, Kanishka B., Brian C. O’Neill, Stephanie TD. Waldhoff, and Claudia Tebadli. 2023. “Non-parametric projections of national income distribution consistent with the Shared Socioeconomic Pathways,” Environmental Research Letters 18 044013 DOI 10.1088/1748-9326/acbdb0
Narayanna, G., Badri Angel Aguilar, and Robert McDougal, eds. 2012. Global Trade, Assistance, and Production: The GTAP 8 Data Base. Center for Global Trade Analysis, Purdue University. Available at https://www.gtap.agecon.purdue.edu/databases/v8/v8_doco.asp
Nordhaus, William D. 2016. “Projections and Uncertainties about Climate Change in an Era of Minimal Climate Policies.” Cowles Foundation Discussion Paper no. 2057. Cowles Foundation for Research in Economics, Yale University, New Haven, CT. http://cowles.yale.edu/sites/default/files/files/pub/d20/d2057.pdf.
Nordhaus, William D., and Andrew Moffat. 2017. “A Survey of Global Impacts of Climate Change: Replication, Survey Methods, and a Statistical Analysis.” Cowles Foundation Discussion Paper No. 2096. Cowles Foundation for Research in Economics, Yale University, New Haven, CT. http://cowles.yale.edu/sites/default/files/files/pub/d20/d2096.pdf.
North, Douglass C., John Joseph Wallis, and Barry R. Weingast. 2009. Violence and Social Orders: A Conceptual Framework for Interpreting Recorded Human History. Cambridge: Cambridge University Press.
O’Neill, B. C. et al. (2017) The Roads Ahead: Narratives for Shared Socioeconomic Pathways Describing World Futures in the 21st Century. Global Environmental Change 42(January): 169–180. DOI: 10.1016/j.gloenvcha.2015.01.004.
Ohlin, Bertil. 1933. Interregional and International Trade. London: Humphrey Milford. Review at https://www.jstor.org/stable/2224730
Ohnsorge, Franziska and Shu Yu, eds. 2021. “The Long Shadow of Informality: Challenges and Policies.” World Bank Group, Advance Edition.
Organisation for Economic Co-operation and Development (OECD). 2002. Measuring the Non-Observed Economy: A Handbook. Paris: OECD Publishing. doi: 10.1787/9789264175358.
Organisation for Economic Co-operation and Development (OECD). 2015. The Economic Consequences of Climate Change. Paris, France: OECD Publishing. DOI: 10.1787/9789264235410-en.
Orr, Adrian, Malcolm Edey, and Michael Kennedy. 1995. “The Determinants of Real Long-Term Interest Rates: 17 Country Pooled-Time-Series Evidence,” OECD Economics Department Working Papers No. 155. https://www.oecd-ilibrary.org/docserver/375710201525.pdf?expires=1627947121&id=id&accname=guest&checksum=B3DA502258F192E35FD20E304F94C756
Pan, Xiaoming. 2000 (January). "Social and Ecological Accounting Matrix: an Empirical Study for China," paper submitted for the Thirteenth International Conference on Input-Output Techniques, Macerata, Italy, August 21-25, 2000.
Patel, Dev, Justin Sandefur, and Arvind Subramanian. 2021. “The New Era of Unconditional Convergence,” Center for Global Development Working Paper 566. https://www.cgdev.org/publication/new-era-unconditional-convergence.
Pennings, Steven. 2020. Long Term Growth Model (LTGM v4.3). Available at https://pubdocs.worldbank.org/en/133191589476085869/Model-Outline-V4-3.pdf
Pesaran, M. Hashem and G. C. Harcourt. 1999. Life and Work of John Richard Nicholas Stone https://www.jstor.org/stable/2565945. Available at http://www.econ.cam.ac.uk/faculty/pesaran/stone.pdf.
Piermartini, Roberta and Robert Teh. 2005. Demystifying Modelling Methods for Trade Policy. World Trade Organization Discussion Paper No. 10. Geneva: WTO. https://www.wto.org/english/res_e/booksp_e/discussion_papers10_e.pdf
Pistaferri, Luigi. 2001. "Superior Information, Income Shocks, and the Permanent Income Hypothesis," The Review of Economics and Statistics 82 (3), August: 465-476. Available at http://web.stanford.edu/~pista/restat.pdf.
Prazeres, Tatiana, David Bohl, and Pepe Zhang. 2021. China-LAC (Latin America and the Caribbean): Four Scenarios in 2035. Washington, D.C.: Atlantic Council. https://www.atlanticcouncil.org/wp-content/uploads/2021/05/AC_China_LAC_trade_2035_FINAL.pdf
Pritchett, Lant. 1997. “Divergence, Big Time,” The Journal of Economic Perspectives 11 (3): 3-17. http://www.jstor.org/stable/2138181.
Pyatt, G. and J.I. Round, eds. 1985. Social Accounting Matrices: A Basis for Planning. Washington, D.C.: The World Bank.
Rao, Narasimha D., Petra Sauer, Matthew Gidden, and Keywan Riahi. 2019. “Income Inequality Projections for the Shared Socioeconomic Pathways (SSPs),” Futures 105: 27-39.
Ravallion, Martin. (1995). "Growth and Poverty: Evidence for Developing Countries in the 1980s". Economics Letters, 48, 411-417.
Ravallion, Martin. (2001a). "Comment on Counting the World’s Poor". World Bank Research Observer, 16(2).
Ravallion, Martin. (2001b). "Growth, Inequality and Poverty: Looking Beyond Averages". World Development, 29, 1803-1815.
Ravallion, Martin. (2004). Monitoring Progress Against Global Poverty. Poverty in Focus: International Poverty Center.
Ravallion, M. (2013). How Long Will It Take to Lift One Billion People Out of Poverty? The World Bank Research Observer, 28(2), 139–158. https://doi.org/10.1093/wbro/lkt003
Ravallion, Martin and Shaohua Chen. (1997). "What Can New Survey Data Tell Us about Recent Changes in Distribution and Poverty?" World Bank Economic Review, 11, 357-382.
Ravallion, M., Datt, G., & van de Walle, D. (1991). Quantifying Absolute Poverty in the Developing World. Review of Income & Wealth, 37(4), 345–361. https://doi.org/10.1111/j.1475-4991.1991.tb00378.x
Reinert, R.K.A. and D.W. Roland-Holst. 1997. “Social Accounting Matrices,” in J.F. Francois and K.A. Reinhert, eds. Applied Methods for Trade Analysis. Cambridge: Cambridge University Press, pp. 94-121.
Romer, Paul M. 1994. "The Origins of Endogenous Growth," Journal of Economic Perspectives Vol 8, No. 1 (Winter): 3-22.
Rothman Dale S., Barry B. Hughes, Kanishka B. Narayan, and Willem Verhagen. 2023. “IFs Agricultural Model Documentation” in Pardee Center file “Ag model documentation V26 Jan 2023”.
Rothman, Dale S., Mohammod T. Irfan, Eli Margolese-Malin, Barry B. Hughes, and Jonathan D. Moyer. 2014. Building Global Infrastructure. Vol. 4 of the Patterns of Potential Human Progress series. Boulder, CO, and New Delhi, India: Paradigm Publishers and Oxford University Press.
Sachs, Jeffrey. 2005. The End of Poverty: Economic Possibilities for Our Time. New York, NY: Penguin Press.
Santos Silva, J. M. C., & Silvana Tenreyro. 2006. The Log of Gravity. The Review of Economics and Statistics, 88(4), 641–658. https://doi.org/10.1162/rest.88.4.641.
Santos Silva, J. M. C., & Silvana Tenreyro. 2011. Further simulation evidence on the performance of the Poisson pseudo-maximum likelihood estimator. Economics Letters, 112(2), 220–222. https://doi.org/10.1016/j.econlet.2011.05.008.
Schneider, F. (2007): Shadow Economies and Corruption all Over the World: New Estimates for 145 Countries.Economics, 2007 (1), July 2007 (2007-2009): 66 pages. https://www.researchgate.net/publication/23755510
Schneider, Friedrich and Dominik H. Enste. 2000. “Shadow Economies: Size, Causes, and Consequences.” Journal of Economic Literature 38: 77—114. doi: 10.1257/jel.38.1.77
Schneider, F., A. Buehn, and C. E. Montenegro. 2010. “Shadow Economies All over theWorld: New Estimates for 162 Countries from 1999 to 2007.” Policy ResearchWorking Paper 5356, World Bank, Washington, DC.
Scott, Andrew C., José R. Solórzano, Jonathan D. Moyer, and Barry B. Hughes. 2022.“The Future of Artificial Intelligence,” International Journal of Artificial Intelligence and Machine Learning 2 (1): 1-37. https://doi.org/10.51483/IJAIML.2.1.2022.1-37.
Shapiro, Matthew, D. and Joel Slemrod. 2003. "Consumer Response to Tax Rebates," American Economic Review 93(1):381-396. https://www.aeaweb.org/articles/pdf/doi/10.1257/000282803321455368
Shepherd, David, Rebeca I. Muñoz Torres, and George Saridakis. 2019. “Monetary policy rules with PID control features: evidence from the UK, USA, and EU,” International Review of Applied Economics 33 (6): 737-755. DOI: 10.1080/02692171.2019.1585766
Solow, Robert M. 1956. “A Contribution to the Theory of Economic Growth.” Quarterly Journal of Economics 70(1): 65–94. DOI: 10.2307/1884513.
———. “Technical Change and the Aggregate Production Function.” Review of Economics and Statistics 39(3): 312–320. DOI: 10.2307/1926047.
Stern, Nicholas. 2007. The Economics of Climate Change: The Stern Review. Cambridge, UK: Cambridge University Press.
Stone, Richard. 1986. "The Accounts of Society," Journal of Applied Econometrics 1, no. 1 (January): 5-28.
Sumner, Andy, Chris Hoy, and Eduardo Ortiz-Juarez. 2020. Estimates of the Impact of COVID-19 on Global Poverty. UNU-WIDER. WIDER Working Paper. https://www.wider.unu.edu/node/237051 (May 11, 2020).
Syrquin, Moshe, and Hollis Chenery. 1989. “Three Decades of Industrialization.” The World Bank Economic Review 3 (2): 145–81.
Tanzi, Vito (1980): "The underground economy in the United States: Estimates and implications," BancaNazionale del Lavoro, 135:4, pp. 427-453.
Tanzi, Vito (1983): "The underground economy in the United States: Annual estimates, 1930-1980," IMF-Staff Papers, 30:2, pp. 283-305.
Taylor John B. 1993. “Discretion versus policy rules in practice,” North-Holland: Carnegie-Rochester Conference Series on Public Policy 39:195–214. Available at https://web.stanford.edu/~johntayl/Onlinepaperscombinedbyyear/1993/Discretion_versus_Policy_Rules_in_Practice.pdf
Taylor, Lance. 1979. Macro Models for Developing Countries. New York: McGraw-Hill.
Thorbecke, Erik. 2001. "The Social Accounting Matrix: Deterministic or Stochastic Concept?", paper prepared for a conference in honor of Graham Pyatt's retirement, at the Institute of Social Studies, The Hague, Netherlands (November 29 and 30). Available at http://people.cornell.edu/pages/et17/etpapers.html.
Tiffen, Mary. 2003. “Transition in Sub-Saharan Africa: Agriculture, Urbanization and Income Growth,” World Development 31 (8): 1343-1366. doi:10.1016/S0305-750X(03)00088-3
Tinbergen, Jan. 1962. Shaping the World Economy. New York: The Twentieth Century Fund.
United Nations Economic Commission for Europe (UNECE). 2008. Non-Observed Economy in National Accounts: Survey of Country Practices. New York and Geneva: UNECE.
United Nations Economic Commission for Europe (UNECE). 2021. In-depth review of measuring the Non-Observed/informal economy. New York and Geneva: UNECE. ECE/CES/BUR/2021/OCT/3. https://unece.org/sites/default/files/2021-10/03_In-depth%20review%20of%20measuring%20informal%20economy.pdf
van der Mensbrugghe, Dominique. 2011. “LINKAGE Technical Reference Document, Version 7.1.” World Bank, Washington, DC. http://siteresources.worldbank.org/INTPROSPECTS/Resources/334934-1314986341738/TechRef7.1_01Mar2011.pdf.
van der Mensbrugghe, Dominique. 2019. “The ENVironmental Impact and Sustainability Applied General Equilibrium (ENVISAGE) Model, Version 10.01.” Purdue University: The Center for Global Trade and Analysis.
Wagner, Adolph. 1892. Grundlegung der Politischen Ökonomie. Leipzig, Germany: C. F. Winter.
Walmsley, Terrie, and Carrico, Caitlyn. (2014). Disaggregating Labor Payments in the GTAP 8 Data Base. https://www.gtap.agecon.purdue.edu/resources/download/7088.pdf (Last access on July 12, 2018)
Weingarden, Alison and Marinos Tsigas. 2010. Labor Statistics for the GTAP Database. https://www.gtap.agecon.purdue.edu/resources/download/4700.pdf (Last access on 07/12/2018). Abstract athttps://www.gtap.agecon.purdue.edu/resources/res_display.asp?RecordID=3248
West, Geoffrey. 2017. Scale: The Universal Laws of Life, Growth, and Death in Organisms, Cities, and Companies. Penguin.
Woltjer, Geert and Marijke Kuiper. 2014. “The MAGNET Model: Model Description,” Wageningen: LEI Wageningen UR. https://www.magnet-model.org/MagnetModuleDescription.pdf.
World Bank. (1990). World Development Report 1990. New York, NY: Oxford University Press.
World Bank. (2001). World Development Report 2000/2001: Attacking Poverty. New York, NY: Oxford University Press.
World Bank. 2021. “PovcalNet.” PovCalNet. http://iresearch.worldbank.org/PovcalNet/povOnDemand.aspx (May 4, 2021).
World Development Indicators. n.d. Washington, D.C. :The World Bank. https://datacatalog.worldbank.org/dataset/world-development-indicators (Last access on July 12, 2018).
Yotov, Y. V., Piermartini, R., Monteiro, J. A., & Larch, M. 2016. An advanced guide to trade policy analysis: The structural gravity model. Geneva: World Trade Organization. https://doi.org/10.30875/abc0167e-en
Yuki, Kazuhiro. 2007. “Urbanization, informal sector, and development,” Journal of Development Economics 84: 76-103. doi:10.1016/j.jdeveco.2006.09.004
Zhang, Jie, and Junsen Zhang. 2005. “The Effect of Life Expectancy on Fertility, Saving, Schooling and Economic Growth: Theory and Evidence*.” Scandinavian Journal of Economics 107(1): 45–66. doi: 10.1111/j.1467-9442.2005.00394.x.
Zhang, Jie, and Junsen Zhang. (2009). "Longevity, Retirement, and Capital Accumulation in a Recursive Model with an Application to Mandatory Retirement." Macroeconomic Dynamics 13: 327-348.
12 Appendix A: Data and Initial Conditions
12.1 Initializing the Country and Global SAMs: The Preprocessor
Preparing an initial data load for a model sometimes requires almost as much work as does creating and maintaining the dynamics of the model. Data inconsistency and data holes require attention; in a model like IFs with physical representations of partial equilibrium sectoral models (agriculture and energy) as well as a general equilibrium multi-sector model represented in value terms, there is the also the need to reconcile the physical and value data.
Creation of a data preprocessor within IFs moved the project long ago from manual handling of issues around data loads to automatic, algorithm-based processing. The preprocessor greatly facilitates both partial data updates as better data become available and rebasing of the entire model to a new initial year (such as the rebasings from 2005 to 2010 or 2015 to 2017). The preprocessor works with an extensive raw data file for all areas of the model, using data gathered for an historical period (most often from 1960, sometimes back further, and when values are unavailable from the earliest data we can find) through the most recent year available. This allows any user to create an historical data load for any desired base year up to and including the most recent data available. As well as periodic normal model basing for forecasting, this feature has been used for the purpose of historical validation analysis starting from, for example, 1960 or 1995; features within the interface facilitate comparison of historical runs with data.
It is not the purpose here fully to document the preprocessor, but a summary description of it generally is important (see Hughes with Irfan 2013 for more early detail) before turning to it for elaboration of economic data preparation. In general, the pre-processing system, when activated from the main menu of IFs, begins with demographics, and imposes total population data on the cohort-specific data by normalizing cohort numbers to the total. The preprocessor reads values for a wide range of population-related variables: total fertility rate, life expectancy, crude birth rate, crude death rate, urban population, migration etc. IFs uses cross-sectionally estimated relationships to fill holes in such data (generally with separate functions for the 1960 (historical base) and 20xx (future) data loads). Most often, functions driven by GDP per capita at PPP have had the highest correlations with existing data; the best functions have often been logarithmic, because the most rapid structural, developmental change occurs at lower levels of GDP per capita (Chenery 1979; Hughes 2001). The philosophy in demographics and in subsequent issue areas in the preprocessor is that values for all countries in IFs will come from data when they are available, but they will be estimated when not available.
The preprocessor then proceeds to the agricultural and energy issue areas. In agriculture, the preprocessor reads data on production and trade. It aggregates production of various crops into a single crop production variable used by the model. It similarly aggregates meat and fish production for the model. It computes apparent consumption. It reads data on variables such as the use of water and on the use of grain for livestock feed. It uses estimated functions or algorithms to fill holes and to check consistency (for instance, checking grain use against livestock herd and grazing land data).
In energy, the preprocessor reads and converts energy production and consumption to common units (billion barrels of oil equivalent). It checks production and reserve/resource data against each other and adjusts reserves and resources when they are inconsistent. Null/missing production values are often overridden with a very small non-zero value so that a “seed” exists in a production category for the subsequent dynamics of the model (a technique used by the Interfutures model of the OECD). World energy exports and imports are summed; world trade is set at the average of the two and country-specific levels are normalized to that average.
The outputs from processing of agricultural and energy data become inputs to the economic stage of pre-processing. The economic processing begins by reading GDP at both exchange rates and purchasing power and saving the ratio of the two for subsequent use in forecasting. The first real stages of economic data pre-processing center on trade. Total imports and exports for each country are read; world sums are computed and world trade is set at the average of imports and exports; country imports and exports are normalized to that global average. The physical units of agricultural and energy trade are read and converted to value terms. Data on materials, merchandise, service, and ICT trade are read. Merchandise trade is checked to assure that it exceeds food, energy, and materials trade, and manufactures trade is identified as the residual. All categories of trade are normalized. When this process is complete, the global trade system will be in balance. The use in IFs of pooled trade rather than bilateral trade makes this easier, but a similar process could be used for bilateral trade with Armington structures.
The processes for filling the SAM with goods and services production and consumption, and with financial flows among agent-classes follow next. More information can be found in the body of the economic model documentation. The preprocessor then moves on to other models in the integrated IFs system, including education, health, infrastructure and socio-political ones.
See Hughes and Hossain (2003 for earlier documentation on the SAM and also its initialization in the preprocessor. See Hughes with Irfan (2013) for earlier documentation on the preprocessor.
12.2 Economic model preprocessor
This Appendix documents the preprocessor as it has been structured in versions of IFs programmed in Visual Basic. The structure of the preprocessor in the .NET language has been changed quite substantially for reasons including processing efficiency. Although the structure of subroutines and code has been changed by that migration, the data files used, sequences of calculation, and processes for reconciling diverse data series and filling data holes is largely the same.
While the focus here is on the portions of the preprocessor associated directly with the economic model nexus (situated mostly in a preprocessor module called DataEcon), the explanations of approach and some of the text provide insights into the considerably larger preprocessor serving all models in the IFs system (with many other modules named Dataxxx). In the focus here on broadly elaborating the economic model nexus, the following numbered subsections address the following elements of the economic model preprocessor:
- Laying of some foundational pieces. It includes several somewhat disparate elements of data reading and processing that provide information that are needed as the preprocessing proceeds. These elements include reading of GDP, splitting of GDP into value added by sector, initializing the labor market, mapping of international economic flows (notably remittances, foreign aid, and trade), sizing other domestic final expenditure components, and determining informal and shadow economy sizes
- Movement into input-output matrix structure by development level. This facilitates linking of aggregate final demand (also read in section sub-section) to required intersectoral flows and will help in building the structure of final demand by origin sector.
- SAM elaborating representation of revenue and expenditure flows. The fiscal patterns of the final demand agents (households, government and firms) are a large part of the social accounting matrix. IFs gives special prominence to revenues and expenditures of government because of their importance in policy analysis explorations.
- Specification of asset and debt stocks. The IFs structure uses flows to raise or lower stock levels and stocks to provide signals for changes in flows.
- Wrapping up important flow variable initializations, including for variables like economic growth rates, tax rates, and poverty rates.
- Writing initializations to files for use in forecasting.
The discussion that follows sometimes deviates from the sequential logic of code in the preprocessor in order more coherently to present economic logic.
12.3 Foundations
The full preprocessor system for preparing initial year data to rebuild the base case of IFs is controlled by the function frm_RebBase, which is called by the user with the Rebuild Model Base sub-option of Extended Features on the main menu of IFs. That function proceeds by calling others in sequence named DataPop, DataAgri, DataEner, DataEducate, DataInfra, DataGovCon, DataEcon, and so on across the other models within the IFs system. Although most of the code controlling the economic model nexus is in DataEcon, there are other elements of it elsewhere. In particular, DataGovCon is important because of the emphasis that IFs places on elaborating expenditures and revenue of government (given its importance in most policy analyses).
12.3.1 GDP and GDP per Capita
Most basically, a subroutine in DataEcon called ProcessEconomicWeights is devoted to filling values for GDP and GDP per capita (both at MER and PPP) for all countries (or sub-country units) of IFs. GDP at MER and GDP per capita at PPP are two of a very small number of “essential data series” in the IFs database (IFsHistSeries.mdb) because GDP and GDP per capita (both at MER and PPP) are necessary for specifying country size and development level. They are widely used throughout the rest of the preprocessor to estimate values of variables with data holes, especially common for economically less developed countries. Because they are needed across the preprocessor and interact with population size, the ProcessEconomicWeights routine within DataEcon is actually called from DataPop, the first module of the preprocessor; doing that makes all four economic variables plus population size (another essential series) available across the entire preprocessor.
12.3.2 Labor
The labor market within IFs is effectively a submodel in itself and has its own documentation (Hughes and Irfan 2016). As such, the discussion of labor within this document is overlapping with that separate document, which also identifies data sources and treatment. In brief, however, because also of the overlap of labor with both demography and economics, it is the population data preprocessor code (DataPop) that initializes key labor variables, primarily from data of the International Labor Organization (ILO). Those are the size of the labor force, the portion of that which is female, the separate and combined labor participation rates of males and females above the age of 15, the unemployment rate, and a labor wage sex ratio. Further data series initialized in DataPop include the rates of informality for both males and females and the portions of male and female workers who are employed in agriculture.
For data on the demand side and the construction of labor demand functions in the model proper, we use data from the Global Trade Analysis Project. The wage variable used in the equilibration algorithm of the model is an index anchored to the base year.[12] A subsequent sub-section of this appendix section elaborates further conceptual and data issues around labor.
12.3.3 Government consumption expenditures
The call of DataGovCon precedes that to DataEcon because of the substantial code that is required to read and process the full set of governmental expenditures for IFs and the importance of having governmental consumption data when the preprocessor subsequently turns to initialization of final demand values in the social accounting matrix. DataGovCon calls ProcessGovConsumptionData, which in turn calls RecomputeGovConOutput. The routine does the work of reading, cleaning, and saving data on government spending in military, health, education, research and development, core infrastructure elements (those represented physically in the IFs infrastructure model), and other infrastructure. The process draws directly or indirectly on a wide range of data sources. For example, military spending data taken from the WDI (SeriesGovtMil%GDPWDI) come originally from the Stockholm International Peace Research Institute (SIPRI) and earlier drawn from the U.S. State Department’s Arms Control and Disarmament Agency. Health spending (SeriesGovtHl%GDP and SeriesHealthExpTot%GDP) come from the World Health Organization via WDI, with private health expenditures (SeriesHealthExpPriv%Tot) coming from the same source. T
Further information on health spending to help differentiate total government and central government (SeriesGovtCalcHelathTot%GDP and SeriesGovtCalcHealthCen%GDP) come from the IMF’s Global Financial Statistics via WDI. The same IMF/WDI sources provide total and central education spending (SeriesGovtCalcEdTot%GDP and SeriesGovtCalcEdCen%GDP), while UNESCO provides a series on total general government spending (SeriesGovtEdPub%GDP). R&D expenditures (seriesR&D%GDPWDI) come from the United Nations Educational, Scientific, and Cultural Organization via WDI.
Note that this DataGovCon function draws separately on data for total national expenditures and those of central government whenever possible (notably for health and education where local governments are most likely to have substantial spending), setting up the potential for later identification of those by local governments (sub-regions of countries and potentially even urban governments).
Data for many countries is missing in these sources and hole filling is done with functions mostly using GDP per capita at PPP and/or years of adult educational attainment).
Infrastructure spending is even more complicated in terms of data sources and is initialized separately in the infrastructure preprocessor code; DataInfra provides values for cINRAINVESTNEW and cINFRAINVESTMAINT across all of the individual physical infrastructure categories and RecomputeGovConOutput simply sums these to a GExpInfra variable. A hard-coded function with CGDPPCP is used to compute GExpInfraOther.
Resultant values from DataGovCon for all government spending categories are saved in the GovConsumptionOutput table of IFs.mdb for later use within the preprocessor building of the final demand structure of the broader social accounting matrix, as discussed later.
12.3.4 Basic structure of DataEcon
Moving next to the call within frm_RebBase of DataEcon, its core structure within ProcessEconomicData involves calls to several routines in sequence. The primary routine is RecomputeEconomicOutput, followed by a call to RecomputePovertyOutput, both to be discussed in subsequent subsections. Basically, both of these routines read extensive sets of data files at the country level and process the data (including hole-filling and value reconciliation across data series) and output clean, country-specific values to data files within IFs.mdb.
But IFs has long gathered and stored data on a country basis and especially in its earlier years the model runs did not forecast variables for all countries. In fact, in early years, the model produced forecasts for 10 global regions via aggregation of data for all member countries. For quite a long time now, IFs essentially has also forecast for all countries. Yet, the model logic allows still for the aggregation to collective groupings and for that purpose the model calls routines RedetermineEcoBase and RedeterminePovertyBase to take care of this. Those routines also help when individual countries have been broken down into subunits (provinces, states, districts, etc.), facilitating the roll-up of data for those subunits into what continue to called regions for these legacy reasons, even when the end result may be countries in reality.
Similarly, the logic moves to RecomputeGovConAdjOutput and RedetermingGovConAdjBase for the government consumption data. And finally, it moves to RecomputeEcDyadicOutput and RedetermineEcDyadicBase to handle dyadic variables within IFs.
12.3.5 Value added by sector
Continuing with foundational pieces and moving next to the call within DataEcon of RecomputeEconomicOutput, the division of GDP (at MER) into the 6 value added sectors of IFs is complicated by the fact that the data on value added are available to us from the WDI most completely for agriculture, industry, services, and ICT, with less full coverage for manufacturing, and none for other primary materials. In general, hole-filling is done with cross-sectionally estimated functions against GDP per capita at PPP.
If the manufacturing value is null, industry is split into energy, other primary materials, and manufacturing proportional to the country’s exports of each. Values for ICT are subtracted from total services to leave a remainder service sector value for the model. After all such calculations and adjustments, the sum across the six sectors is normalized to GDP.
12.3.6 International economic flows
The second section of the economic preprocessor (built across sections in the RecomputeEconomicOutput routine) moves into the social accounting matrix. It begins with a focus on the final demand block of that structure. Within final demand, it focuses initially on international flows because those flows (including remittances and foreign aid) are important to the income and expenditures, and thus to the final demand patterns of firms, households, and government.
Another reason for an early look at international flows is that the data sources for those flows tend to be quite diverse (although the World Bank’s World Development Indicators and various series from the International Monetary Fund and the OECD are prominent). The diversity of data sources and the common volatility of the flows over time means that there can be considerable complication in creating a consistent data load for the base year.
12.3.6.1 Aggregate international flows
The subroutine named ReadAndProcessIntlFlows handles the treatment of international financial flows. It first reads data on remittances and foreign aid sent and received. It reads remittances and foreign aid as percentages of GDP Because foreign aid receipts can vary considerably year-to-year it averages the most recent four-year values. The routine then balances the global totals of absolute flows for each, which are very different in both cases, given the data sources and quality. Remittance and aid flows are often much bigger portions of the GDP in lower-income countries than in high-income ones, so the routine creates the balance by adjusting values for high-income countries where changes will have much less impact on the broader national accounts and economies.
Foreign aid receipts present a special complication for this process because aid receipt data is net of aid-related loan repayments. Although the model reads a variable representing aid grant receipts as a percentage of total government revenue (putting it into and aid share variable), it does not currently differentiate aid loans and grants as a percentage of GDP and simply bounds the receipt data to be positive; enhancement with representation of grant versus loan aid could be helpful and may be possible.
The routine then reads data on total exports and imports, without normalizing at this time (to be done later). Again, it reads these as a percentage of GDP, averaging the last three years for exports and the last four years for imports, but without normalizing them globally, a process that occurs later in the preprocessor’s flow.
The routine then reads data on the national current account balances. Those data are useful in two ways. The first is to examine the consistency of data across the various elements of the current account, and the second is to use the current account balances to make some adjustments in trade when levels of it appear very inconsistent with the current account.
With respect to consistency of the data, trade, remittances, and foreign aid are the dominant portions of the current account in almost all countries and allow the computation of a “bottom-up” estimate of that current account (CURACTDATABOTTOM). The preprocessor puts the database’s value of current account into CURACTDATATOP for comparison in model use with that bottom-up estimate of current account. Moreover, the database contains series representing receipts and payments of balance-of-payment related international income flows and these are read into CURACTNETPRI and CURACTNETSEC. Primary income flows include income that national residents earn from or pay to the rest of the world (e.g. wages and dividends), while secondary income flows include transfers such as remittances and foreign aid.[13] Theoretically, the sum of the trade balance and the net primary and secondary income flows should equal the current account balance in historical data, and the flexible displays in IFs verify that they generally do. Exceptions are countries like Equatorial Guinea and Somalia with very limited data on current account data and/or its components in recent years.
The current account calculation in IFs forecasting is built upwards from trade, remittances, and aid, thus omitting the elements of primary income flows. That omission from IFs data and forecasting representation of primary international income flow components including wages and dividends is not problematic for most countries, because those tend to be very small relative to trade balances and net secondary flows (especially remittances and foreign aid). An exception is Timor-Leste because its data show very large net inflows of primary income in years from 2006 through 2020, generally more than offsetting large deficits in trade. In the future it might be useful to add international flows of wages and dividends to IFs forecasting.
The second use of data on current accounts and its components is to give some priority to that on current accounts and to adjust imports and or exports so as to provide greater bottom-up consistency with that current account data. Adjustments are made to total imports and/or exports in a sequence of steps that use rules to adjust them where there appears most likely to be error or temporary volatility.
12.3.6.2 Trade flows by sector
Following the reading and processing of these international flows, a subroutine named ReadAndNormalizeTradeData reads trade data for each of the model sectors (six as of this writing) and assures that trade in them is consistent with total imports and exports.
It begins by examining agriculture and energy trade (converting physical flows of energy processed in its preprocessor to value terms) against total imports and exports to make sure there is head room enough for them, creating it if necessary. It then normalizes total global exports and imports to same value.
It proceeds to reading merchandise and service trade; it also reads arms imports but does nothing with it in terms of analysis against exports or share of merchandise trade. It normalizes the total of merchandise and service trade to total trade within each country. It computes and normalizes ICT trade, removing it from services. It computes agricultural trade as sum of crop, meat and fish trade as exported to AgriOutput earlier. It checks agricultural trade against merchandise total to again assure headroom. It calls RecomputeAgriOutput to handle any changes in agricultural trade. It does same check of energy trade against remaining merchandise trade and normalizes global totals; does it a second time in case energy trade was pushed above remaining merchandise limit. It undertakes the same process for materials trade with respect to remaining merchandise trade. Thereafter it assigns remaining merchandise trade to manufactures.
Given the various adjustments to total imports and exports in the process of assuring headroom, it undertakes one last check of global import and export totals to assure that they are very close to identical (within 2%).
12.3.7 Expenditure Components
While the setting of initial conditions for value added provided foundational variable representation for the supply side elaboration of GDP, on the final demand side of GDP it is important to look at the trade balance (exports minus imports, part of the international economic flows elaborated above) and also at household consumption, government consumption, and investment. The preprocessor looks to three series for general agent category expenditure (SeriesHouseCon%GDP [183 countries], SeriesGovCon%GDP [174 countries], and SeriesInvestGrCapForm%GDP [175 countries], all from the World Bank and OECD via WDI). These provide data values for household consumption, government consumption (not including government transfers, so not all of government expenditures), and gross capital formation (investment), all as percentages of GDP. Holes are filled via cross-sectional functions with GDP per capita at PPP and each of the values is bound with upper and lower limit percentages of GDP because sometimes recent values are anomalies.
These series provide foundation for the variables CPCON, CGCon, and CINVEST, respectively. Using the content of the variables filled earlier for government consumption by destination (GExpDef, GExpEd, etc.) and assuming at least 1 percent of GDP will be spent on the “other” category of government consumption in IFs, the code assures that CGCon will be the maximum of the sum by consumption category and the value read in the data series. We shall see blow in the elaborated discussion of the social accounting matrix the review of government consumption in the context also of transfer payments from the government and the revenue structure for it.
The health and education expenditures are assigned to CGovConLocal but CGCon itself remains general government (central plus local).
12.3.8 Informality
Something of a digression from the elaboration of the formal SAM structure in IFs is initialization of variables related to economic informality, including those that the forecasting model identifies with informality terminology (for instance the levels for females and males and the levels for labor in total relative to GDP share) and those that the forecasting model identifies with shadow economy terminology. For all of this there is a call to the ReadInformalEconomy routine.
12.4 Input-Output Structure and Basic Final Demand
Building on the various foundational pieces (and some elaborations of the economic nexus model such as informality that are not part of the core social accounting matrix structure), the logic of the preprocessor turns to the input-output matrix that sits in the upper left-hand corner of matrix representations because its direct manifestation in terms of intersectoral flows links the levels of value added that sit below in on the left and the values of final expenditure by agent categories (households, firms (notably investment), and government that sit on its right (see again Table 3.1 in the textual description of the forecasting model).
The InputOutputData routine called at this point draws very heavily on GTAP data (as well as some from the WDI). It builds eight generic input-output coefficient matrices for the six sectors of IFs based on the much larger country and regional matrices from GTAP, putting them into the IOMatricesCalc table IFs.mdb (IOMatricesCalcHist for earlier years). It also fills matrices of skilled and unskilled labor by IFs sector. Further, it processes GTAP data on capital by sector and country and land by country, putting information on those factors of production for each country into the GTAPValueAdded table of IFs.mdb; it further computes generic profiles for labor across the same GDP per capita thresholds as for IO coefficients, putting those into the IOLaborCoefs table. In short, the InputOutputData routine sets up the representation in IFs of changing technologies of production with economic development, both the use of factors of production (notably labor and potentially capital) and the intersectoral flow patterns. Because this capacity exists in the preprocessor, IFs can process new GTAP releases and update these variable sets as underlying data implicitly represent changing technological patterns.
The input-output matrix structure facilitates linking of aggregate final demand to intersectoral flows and helps in computing the structure for the sectors of final demand origin.
12.5 SAM Elaboration: Expenditure and Revenue Flows of Agents
Following the initialization of a disparate set of foundational pieces, including GDP, GDP per capita, value added, the input-output structure, international economic flows, other expenditure components in aggregate, and informality, the logic of the preprocessor turns next to elaborating its representation of final demand. The fiscal revenue and expenditure patterns of the final demand agents (government, firms, and households) are a large part of the social accounting matrix.
The first step in handling the expenditure and revenue patterns of the three agent categories is to look at key overall expenditure patterns across them. A call is made to ReadGovExp to retrieve values that were saved earlier in the GovConsumptionOutput table of IFs.mdb by the call to DataGovCon preceding the call to DataEcon; those values are for the specific categories of government consumption: GExpDef, GExpHl, GExpEd, GExpRandD, GExpInfra, GExpInfraOther, GExpHlLocal, and GExpEdLocal. Note: The call to ReadGovExp is actually intermixed with the foundational pieces described earlier, but the values it read earlier are used only at this point. There are other examples where the flow of reading and processing in the economic preprocessor is not always consistent with what might be a stronger logic of sequence.
More generally, IFs gives special prominence to expenditures and revenues and expenditures of government because of their importance in policy analysis explorations, and the first subsection below identifies data sources and initialization processes. Subsequent subsections turn to firms and households.
12.5.1 Government finance
Finding data for all counties in IFs to initialize the financial flows of the social accounting matrices with the preprocessor has been challenging since its first development in IFs (Hughes and Hossain 2003).
A large portion of the government finance data in the International Futures model is originally from the International Monetary Fund (IMF Government Finance Statistics, GFS at http://www.imf.org/external/data.htm). That source has increasingly provided important series including the ability to begin differentiating central and local government revenues and expenditures, important in IFs as we progressively represent states, provinces or other jurisdictions within countries. At this writing, most analysis is done at the general or total government level (central plus local). Local variables are rather preliminary and the distinction is primarily made using data from the IMF’s GFS.
Because of the ease of their collection, IMF data published in the World Development Indicators (WDI) dataset are heavily used in the IFs model. We also use databases published by global think tanks. For example, the International Center for Tax and Revenue (ICTD) has compiled a long series on taxes and revenues, and the Global Trade and Analysis Project has collected/developed much data. The preprocessor pulls revenue data from a large set of data series in IFsHistSeries.mdb, namely SeriesTaxCorp%Tot, SeriesTaxSocSec%CurRev, SeriesTaxGoodSer%CurRev, SeriesTaxImportDuties%Rev, SeriesTotRev%GDPIMF, SeriesGovRevOECD%GDP, SeriesGovtCalcRevTot%GDP, SeriesGovtCurRev%GDP, SeriesGovtCalcRevCen%GDP, SeriesGovtGenRev%GDPFM. It similarly pulls expenditure data from a large set, namely SeriesGovSSWelBen%Exp, SeriesGovtPension%GDP, SeriesGovTotalOutlays%GDP, SeriesGovtCalcExpendTot%GDP, SeriesGovExpense%GDP, SeriesGovtCalcExpendCen%GDP, SeriesGovtGenExp%GDPFM. Multiple series are routinely looked at in sequence to fill holes earlier ones, with priority based on judgments about quality and completeness of data coverage, as well as consistency with the conceptual variables in IFs.
As throughout the preprocessor, code reads in data for the model base year from the historical database. When data for the base year are not available the model looks for the most recent data value preceding the base year. When there are no data for a country/region or the available data are not close enough to the model base year, When all such data are unavailable, IFs uses analytical functions to estimate data for the base year. These analytical functions are usually regression relationships formulated with the most recent data on the variable being filled in and a reasonably and strongly correlated driver variable, for example, GDP per capita.
12.5.1.1 Government revenues
In sequence, initial values for IFs variables are determined for total government revenues and central government revenues, with values for local revenues being the residual. The preprocessor opens four different data files from different sources (the IMF, the WDI, and OECD) for data on total government revenue as a percent of GDP and one on central government revenue). The primary source is the IMF and SeriesTotRev%GDPIMF (with data for 181 countries since 1990). If the primary source for total government revenue does not have values for a country, the preprocessor looks to an OECD series (SeriesGovRevOECD%GDP). Those series are highly correlated, as the figure below shows. Continuing to fill holes the preprocessor turns next to a secondary IMF series (SeriesGovtCalcRevTot%GDP), the updating/calculation of which within the IFs team has been discontinued. Finally, the code turns to a function with GDP per capita at PPP. The value taken in this progressive effort is put into a local variable called GovRevTot. After some reality checks on magnitude it is also put into GovRevPerSave.
For the central government expenditures, an IMF series with data on 165 countries is used (SeriesGovtCalcRevCen%GDP) and that or a value from a function is placed into GovRevCen. The difference between total and central government revenues is put into CGovRevLocal.
The preprocessor also looks at the sources of total government revenues, pulling information into CFirmTaxR (SeriesTaxCorp%Tot from the IMF GFS), CSSWelTaxR (SeriesTaxSocSec%CurRev from the WDI, 149 countries), CIndirectTaxR (SeriesTaxGoodSer%CurRev from the WDI, 172 countries) and CTarrifTaxR (SeriesTaxImportDuties%Rev from the WDI, 175 countries). Without a specific data series for them, household taxes are assumed to represent the residual share of total tax revenue (and set at a minimum of 1 percent of GDP)―many lower income countries have not built systems for taxes on households. Whereas most expenditure values are read as percentages of GDP, most revenue values are obtained as percentages of total revenues (total revenue is a percentage of GDP). The code computes adjusted values of all tax rates as portions of domestic revenues, where domestic revenues are the produce of CGCP and GovRevPerSave reduced by CAIDREC.
The model needs base-year tax rates rather than absolute dollar values and those tax rates need to be applied to the total incomes of firms and households. At this point in the code sequence, however, the values for annual FDI and portfolio flows have not been initialized (that is done when the logic turns to stock variables and simultaneously averages several years of FDI and portfolio flows as a percentage of GDP to estimate an appropriate base year value). The preprocessor assumes that those flows affect the value of firm income, in particular, and therefore waits until after their calculation to compute the final tax rates: CFirmTaxR, CIndirectTaxR, CTDariffTaxRSec (by sector), CHHTaxRUnskilled and CHHTaxRSkilled.
12.5.1.2 Government expenditures
On the expenditure side, data are more complete for central government and values are determined for local and total government with relatively sparse data. The preprocessor reads total government expenditures from SeriesGovtCalcExpendTot%GDP (IMF, 97 countries) and central expenditures from SeriesGovExpense%GDP first (WDI from IMF etc., 169 countries) and SeriesGovtCalcExpendCen%GDP second (IMF, 149 countries) The graphic below shows the relationship between the two series used for central expenditures and the higher values for European countries of the former clearly suggest its superiority.
When both total and local expenditure values exist in the data, local is again the residual. If total expenditures do not exist, then local is computed based on some data about the growth of local revenues and expenditures in North, Walli and Weingast (2009: 10):
In this case, total expenditures are initialized as the sum of central and local. A check is made to assure that total government expenditures exceed the value of total government consumption read earlier, assuming that government transfer payments (welfare and pensions) must be at least one percent of GDP.
Again, direct government consumption (CGovCon) expenditures break down in the categories of military, health, education, infrastructure, R&D, (core) infrastructure, and other infrastructure and those and the variable CGovCon itself were initialized earlier in the foundational pieces of the preprocessor logic. CGovCon is reviewed and set as the larger of the sum from the categories and a its earlier direct specification of it from WDI data (SeriesGovCon%GDP). The preprocessor assures that GOVEXP is at least 1 percent more of GDP than is GOVCON, to make some headroom for government transfers.
Total government expenditures in the IFs model are defined as the sum of direct consumption and transfers, in turn defined as the sum of social security/welfare payments (GOVSSWEL) and pension payments (GOVHHPenT). Data on government transfers in these two categories are not very strong. We use WDI data in SeriesGovSSWelBen%Exp (139 countries), and SeriesGovtPension%GDP (166 countries), respectively. The data read by IFs on social benefits/welfare from SeriesGovSSWelBen%Exp are treated as if they include expenditures on pensions and thus constitute all of transfer payments. In the model proper these data help initialize the variables GOVHHTRN (transfers from government to households, again intended to be the sum of social security payments and pension payments) and GOVHHPENT (payments of pensions alone).
A block of code compares the sum of GOVCON and the values in the SeriesGovSSWelBen%Exp series with total government expenditures (CGovExp). If the sum is less it boosts GOVCON and if the sum is greater it reduces transfer payments if those payments exceed the excess or again raises the total expenditures.
12.5.2 Balancing the final demand side
At this point it is possible to review the final demand side of the economy in aggregate. The foundational specifications of the preprocessor specified values as a percentage of GDP for household consumption (CPCON), investment (CINVEST), and government consumption (CGCon), as well as for the trade balance (exports minus imports). The governmental finance elaboration has potentially revised the value of CGCon. Together the identity of GDP as the sum of these final demand components should be maintained and a block of code leaves trade unchanged while normalizing CPCON, CGCon, and CINVEST to the residual of 100 percent of GDP.
12.5.3 Sectors of origin for final demand components other than trade
Sectors of government consumption such as military, health, and education expenditures do not correspond to the sectors of value added and production such as agricultural goods, manufactures, and services. In balancing the SAM it is necessary to represent the sectors of origin for total household, government, and investment final demand; trade final demand does automatically correspond to the sectors of origin as represented in the value added vector and the intersectoral flow matrix.
In the absence of clear data on this, the preprocessor identifies the sector of origin for government spending as 10 percent manufactures and 90 percent services. It identifies investment as 50 percent manufactures and 50 percent services.
The largest portion of GDP is household consumption and the preprocessor elaborates its sectors of origin by using the values of the input-output matrix and the value added by sector, both of which have been established already by the preprocessor (foundational pieces). It assumes that households directly consume agricultural goods, energy, manufactures, services, and ICT (leaving out unprocessed raw materials). It uses this information and data on trade plus the country-specific IO matrix to compute sectors of origin for household consumption (pcons), normalizing them to CPCON. Those values become a starting point in the model proper for computing changes in consumption patterns of households over time as economic levels of well-being for them change.
This final piece of analysis of expenditure flows assures that the initial conditions for data in the model do constitute a fully balance social accounting matrix. Dynamics of that matrix depend heavily upon agent-related stocks and the preprocessor turns to those next.
12.6 Country and Agent-Category Debt/Asset Stocks
The magnitudes of debt and asset stocks associated with households, firms, governments, and countries as a whole greatly influence their patterns of revenue and expenditure flows over time. The recursively dynamic structure of IFs builds upon that stock and flow interaction. In particular, the model includes dynamics (using PID controller systems) around total external debt of countries (affecting their exchange rates in trade) and total government debt (affecting the patterns of change in both revenues and expenditures).
Unfortunately, statistical compilations are much more extensive and accurate with respect to flows than they are for stocks. And because of its implications for posing challenges to behavior around flows and the generally stronger database for it, attention to debt is considerably greater than that to assets. It therefore can be challenging to create a structure for the preprocessor that provides initial conditions to the model for debt and asset positions. Fortunately, the long-term dynamics of the model respond much more to changes in stocks over time than to their initial conditions and stock data have become more available over time.
As with flows and for the same policy-analysis-importance reasons, the preprocessor gives disproportionate attention to governmental stocks relative to those of firms and households. It also gives much attention to the international financial stock positions of countries, which significantly interact with debt/asset stocks of governments. Specifically, two stock values are especially fundamental to the model’s flow dynamics (using the PID controller system): national external assets/debt (because it affects exchange rates) and governmental debt (because it shapes changes in patterns of revenue and expenditure). In addition, however, the model initializes a variable for external firm debt. And while it has a variable for household savings stock that affects dynamics around savings and consumption, in the absence of data for that stock the model focuses on change in the stock.
A key data source for stock analysis has long been the World Bank’s International Debt Statistics, released annually. Among other external debt series it provides for low- and middle-income countries (123 of them in 2022) are information on (1) loans from the World Bank, (2) credits from the IMF, (3) national public and publicly-guaranteed debt, and (4) national private non-guaranteed debt. It also provides total external debt, defined as the sum of public, publicly-guaranteed, and private non-guaranteed long-term debt as well as IMF credits and short-term debt. IFs uses those series and associates the first three with government indebtedness and the last with that of firms.
Another key data source is the IMF Global Debt Database, also annual. It provides information on both private and public debt for almost all countries of the world. IFs uses its series for total government debt, external and domestic.
An important source available with respect to net foreign assets is the IMF’s International Financial Statistics. An important conceptual/data issue concerning foreign positions is the distinction between net foreign assets (NFA) and net international investment position (NIIP).[14] The former is a concept related to balance of payments accounting; annual change in NFA is very closely equal to the current account balance, but it is also subject to valuation effects related to changes in the exchange rate and of the asset prices of the national assets and liabilities. NIIP includes both governmental debt and private debt, changes in the latter not always being apparent in the current accounts. The image of countries on these two measures can be very different for reasons including the existence of sovereign wealth funds (SWFs) which can either be integrated into central bank accounting or not. When not incorporated the concepts can have very different values. For instance, in 2021 the value for NIIP of Norway (with an extremely large SWF) was 265 percent of GDP,[15] but its value for NFA in the IMF financial statistics database in 2020 was -29 percent of GDP. In contrast, the database value for NIIP in the US was -65 percent of GDP, but for NFA it was just over 1 percent of GDP. Again for the same years, the value of NIIP for Saudi Arabia was 73 percent of GDP and for NFA is was a very similar 80 percent. To a large degree, changes in exchange rates and therefore effects on trade balances and the current account are driven by NFA and the governmental/central bank position in currency markets. Because exchange rates and trade are key variables in IFs forecasting, the heavier emphasis of its preprocessor is on NFA.
The discussion in the following sub-sections will look in turn at total international debt/asset positions of countries and then at government and firm debt. The actual computation sequence in the preprocessor actually begins with governmental debt to international financial institutions (IFIs) before turning to country debt/assets. The presentation here should facilitate conceptual logics.
12.6.1 International debt/asset positions of countries
There are potentially two ways to initialize base year model values for stocks of external debt, such as government debt to international financial institutions (IFIs), namely and World Bank and the International Monetary Fund, firm debt that might be publicly guaranteed or not, and the total of foreign debt. The most desirable way is to find series that provide those stocks in the various categories and the less desirable way is to estimate those stocks by accumulation of historical patterns of flows over time. Although the latter approach was earlier used by the preprocessor for total external debt and the code still computes accumulations as a hole-filling back-up to data on stocks, availability of more recent IMF and World Bank data make that mostly unnecessary.
Because the signals that various debt/asset positions communicate to changing currency exchange rates and government changes in expenditure and revenue patterns flow largely from the debt side of the debt/asset pictures, the names of most IFs international stock and flow variables represent net debt levels, with negative values of those debts representing net assets. Thus, the signs of key financial stock variables in IFs (net debts) and those in IMF data (net assets) can be reversed.
Another issue is that some data series tend to be somewhat richer on the debt side than for assets. When there are no asset representations in some series of interest to us, the preprocessor sums the total of the debts globally and arbitrarily allocates that sum to higher income countries proportionately to their GDPs.
The following subsections explain the steps taken in the preprocessor to initialize model variables representing international debts/assets of countries.
12.6.1.1 Core international debt/asset variables and data
The model needs net financial debt/asset values of countries to drive exchange rates. The preprocessor has long filled, and the model used, a variable named XDEBTRPA (CXDEBTRPA in the preprocessor). The RPA extension stand for “relative price adjusted” because as country-specific price levels and thus exchange rates change, the value of net foreign debts/assets (and GDP) changes accordingly in the model forecasts. This is especially important for countries like major oil exporters where changes in the value of a very large portion of their economies does change GDP, prices and exchange rates, and currency-based values for net foreign assets.
The legacy representation for filling base year values of XDEBTRPA in the preprocessor relied heavily on accumulating across time and summing across various international financial flows that give rise to net debt or assets. That approach has, however, with few data-poor country exceptions been replaced by the use in the preprocessor of IMF data to initialize XDEBTRPA and also new model variables named XNFA (net financial assets) and XNIIP (net international investment position). The preprocessor uses the data for XNFA (NetForeignAssets%GDP) to fill in initial but opposite-signed values for XDEBTRPA. The use of NFA data to initialize XDEBTRPA for dynamic use in the model is related to the governmental financial responsibility for financing underlying current account imbalances and the interaction of that funding potential with changes over time in the exchange rate, an important equilibrating variable.[16]
For countries without NFA data, the preprocessor looks next to the WDI XDEBT%GDP series to attempt to fill holes in XDEBTRPA and then to the WDI XDebt series. The preprocessor also uses the IMF series NetIIP%GDP to fill the variable XNIIP.
12.6.1.2 Accumulation of current account values for back-up
Only if none of the series accessed help identify appropriate base year values for international indebtedness (XDEBTRPA) does the preprocessor turn to the legacy approach of accumulation across time of as many elements of the current account as are possible to find in the database. Important note: in the preprocessor, the code for computing the indebtedness using the accumulation approach sits above the code first attempting to fill debt/asset variables directly from data series and stores its results into preprocessor variable XDEBTACC (locally in the preprocessor named CXDEBTACC, just as other model variable names initialized in the preprocessor have names there that start with “C” for country).
Again, the current account balance that changes XDEBTRPA over time is defined as the trade balance in goods and services, plus elements of primary and secondary income, The primary and secondary income variables include income on assets (such as rents, interest, profits and dividends), various transfer payments (including foreign aid, government subscriptions to international organizations, pension payments to workers living abroad, and foreign worker remittances to their home countries). As a very rough estimate of base year values for the net debt/asset position of the small number of countries for which NFA is not now available from data, the preprocessor looks to data on two of the most important of these components of current account, namely foreign aid and trade flows. It integrates over time from 1960 through the model’s base year export and import data as well as foreign aid data (minus a portion of that shown by data not to be outright grants and therefore to be loans). The accumulated sums of exports minus imports plus aid loans is then put into the CXDEBTACC variable whenever data from the NFA and other aggregate international debt series are not available. In future revisions of the preprocessor it would be possible to add more newly acquired data on remittances (available for many countries from 1970) to this back-up accumulation variable, but there may not realistically be countries for which that is available and IMF NFA data are not. One last check is done on the value of CXDEBTACC against the sum of indebtedness to the IMF and World Bank to assure that it exceeds that sum. That indebtedness initialization is therefore computed prior to this check even though it is described later in this discussion of international debt and asset variables.
As indicated earlier, it ideally would be the full dynamic use of current account conceptualization and forecasts of component variables that would drive both XNFA and XDEBTRPA (with the opposite sign) in the model proper. That proves complicated in the model because NFA is definitionally changed over time by not just the trade balance component of current account, but by the current account net primary and secondary primary income terms. Yet, IFs does not have a strong forecasting basis for components of the primary term (XCURACTNETPRI in the model) including interest and dividend income. Therefore, the model drives XDEBTRPA with the trade balance plus the aid and remittance flow balances of the secondary income term (CURACTNETSEC). As a way of understanding generally the implications of omitting the primary income term for both current account (CURACT) and XDEBTRPA, the model does compute an estimation of the primary income term (CURACTNETPRI) based on the size of the net balances of contributions/liabilities to governments from the World Bank and the IMF plus the country’s net position with respect to foreign direct and portfolio investment; it applies a typical real interest rate to the ongoing net sum of those stocks to generate that estimate. That value of CURACTNETPRI is used in the calculation of forecast values for XNFA even though it is not included in the value of XDEBTRPA.
12.6.2 Firm external debts/assets
The treatment of firm debt in IFs is limited to external debt (CXFIRMDEBT) rather than internal or domestic, and it is initialized using WDI data on external private non-guaranteed debt (SeriesXDEBTPNG%GDP). Holes are filled with zeros because levels of debt are often very small and non-reporting often will imply debt levels near zero. In the absence of data concerning the countries holding this debt as an asset, the assumption was made that all of this debt should be assigned as assets to governments in developed countries, specified as those with GDP per capita above $10,000.
The preprocessor does not access any possibly-existing series on total firm debt including that in domestic markets.
In the model proper, XFIRMDEBT is computed over time (including first year) as the changing balance of net inward minus outward FDI and portfolio stocks. That calculation effectively overrides the preprocessor’s initialization, which is instead used only in the preprocessor itself for the purpose of computing external government debt as total national external debt minus this external firm debt value from data (a computation described in the next sub-section).
The preprocessor also initializes both inward and outward flows and stocks of foreign direct investment and international portfolio investment, normalizing them so that global totals of inward and outward are identical. These variables are important in model forecasting in and of themselves, but in the case of the stocks also in dynamic computation of external firm debt (XFIRMDEBT). Although the model accumulates change in these initial estimates of firm debt related to foreign direct and portfolio investment, it does not build dynamics of exchange rates or other equilibrating variables around firm debt, reducing the importance of the crudeness of estimates for base year values.
The data for foreign direct and international portfolio investment is taken from the WDI and represents annual inflows and outflows (SeriesXFDIInflows%GDP, SeriesXFDIOutflows%GDP, SeriesXPortBonds%GDP and SeriesXPortEquity%GDP. We do not use stock data for initialization of those but rather rely on integration of flow data to initialize the stock variables of importance in the model.
With respect to the inward (CXFDISTOCK) and outward (CXFDISTOUT) stocks of FDI, the flow series are integrated over 30 years prior to the base year and the totals are limited to two times recent GDP. In addition, however, the preprocessor fills the flow variables passed to the model (CXFDIFIN and CXFDIFOUT) by averaging percentage-of-GDP values of five years up to and including the base year so as to smooth what often is a highly volatile series. In both cases the values are normalized globally to the global sums of incoming stocks and flows.
A very similar process is used for portfolio investment. But to determine inward stocks, two data series of flows are summed, one for bonds (SeriesXPortBonds%GDP) and one for equities (SeriesXPortEquity%GDP). The resultant integrated sum is bound at 50% of recent GDP. Further, in the absence of outward flow data the inward stocks are distributed to countries with GDP per capita above $10,000 proportionately to their GDPs. The same outflow distribution to higher-income countries is made of the inward flows after computing the five-year average of recent flow rate data.
12.6.3 Government total debts/assets
12.6.3.1 Primary government debt/asset variables
Turning from national and firm analysis to the government, four variables are initialized. They are total government debt, and its division between external and domestic government debt, and reserves.
The preprocessor looks to three different series to fill the total government debt variable (CGOVDEBT), important because it is the variable in the model proper that, as a percentage of GDP, drives the equilibration process involving feedbacks that raise or lower revenues and expenditures so as to control the level of debt over time. In priority sequence the data series are SeriesGovtDebtGen%GDPIMF, SeriesGovtDebt%GDPIMF, and SeriesGovtDebt%GDP. While take from the WDI, all come originally, primarily from the IMF. Only if none of those series have data values for a country does it turn to a cross-sectionally estimated function with GDP per capita at PPP. Although only the first of the three data series is defined explicitly as being general debt, the other series are useful in filling hole because in almost all countries central government debt is effectively the same as general government debt (sub-national entities are often proscribed from incurring debt).
Government external debt (CXGOVTDEBT) is computed simply as the difference between total external debt (CXDEBTRPA) and external firm debt (CXFIRMDEBT), both elaborated above. And domestic government debt (CGOVTDEBTD) is simply total government debt minus the external debt.
Although total government debt is the variable of greatest importance to the modeling, the division of it into external and domestic categories has potential interest. So too, does another variable identified as “basic” external government debt (CXGOVTDEBTB), which in the preprocessor is the government’s external debt minus credits that have been provided by the IMF (CXIMFCREDIT) and loans from the World Bank (CXWBLOANS)―both of which the next subsection discusses. The reason for computing that variable in the model is that all debt is not equal. For instance, when debt becomes too large, governments must make hard choices between repayments of debt owed to banks or other governments in support of guaranteed firm debt (or foreign aid received as loans) and debt owed to international financial institutions.
12.6.3.2 Stocks of government debt to IFIs
As suggested above, government debt to IFIs is interesting in itself, but also can be useful (1) as an important component of external government debt, especially in very low-income countries, in case the data series for net foreign debt/assets of any country not provide values and therefore the variable value needs to be estimated; (2) to assure that the values assigned to external government debt (XDEBTRPA) in the process described earlier are at least large enough to be assure inclusion of the debt to IFIs. For these reasons the preprocessor actually computes IFI debt stocks in advance of its computation of total national external debt; the sequence of discussion in this document reverses that order to facilitate organization by actor category.
Using data series from the WDI (SeriesXWBLoans%GDP and SeriesIMFCredit%GDP), the preprocessor initializes total outstanding loans to countries from the World Bank (XWBLOANS) and IMF credits (XIMFCREDIT). In the absence of data on country contributions to these IFIs, the global total of those is allocated to countries with GDPs per capita above $10,000 proportionately to their GDPs. These very rough estimates of IFI contributions are theoretically an asset of the countries and governments making them, but presumably will never be recovered by them for other use.
12.6.3.3 Other government variables
The preprocessor initializes two other variables of potential interest in forecasting. The first is international reserves (CXRESERVES), filled from the WDI (originally IMF) data series SeriesXReserves%GDP. That stock variable provides information on gold, special-drawing rights with the IMF, and foreign exchange holdings of monetary authorities. As a short-term variable subject to rapid change in countries from market speculation about currency strength, it is extremely difficult to forecast reserve holdings over the long-run. Hence the initial conditions can be of interest to model users, but the model does not attempt to forecast them over the long-term. Their percentage of GDP in all countries is allowed simply to converge toward zero before mid-century and the variable has no forward linkages. It is therefore the broader XDEBTRPA variable that drives changes in exchange rates, given its linkage to other IFs variables representing long-term change.
The second additional variable is CXFINUNEXP or finance unexplained (a flow varialble), which is not now dynamically changed in the forecasting side of the model. It is computed in the preprocessor as the difference between internal preprocessor variables named IntlPositionChange and CompIntlPositionChange, intended as two representations of change in national external financial balances that should be roughly equal. IntlPositionChange looks to the sum of annual changes in the two data series on reserves and public and publicly guaranteed external debt. CompIntlPositionChange looks to difference between data-based components of current account (trade balance, foreign aid balance, and worker remittance balance) and capital account (changes in balances of FDI, portfolio investment, and IFI indebtedness). Theoretically the difference between IntlPositionChange and CompIntlPositionChange as a percentage of GDP should be relatively small if all the data series are quite accurate and consistent, so it should be a helpful indicator concerning data quality. In reality, volatility and missing data points make such a comparison at any point in time difficult and of somewhat questionable utility. Moreover, the comparison in the preprocessor was set up using data years 1997-2000 for reserves and external governmental debt, so it is out of date.
In the model proper the flow variable XGOVTDEBTBF similarly compares current and capital accounts and is used annually to update the external government debt stock, augmenting the stock variable XGOVTDEBTB, which is also augmented by the loan portion of foreign aid and net flows from the IMF and World Bank in the computation of XGOVTDEBT. Given much year-to-year volatility in the component variables and its current computation near the turn of the century, there is no real basis for thinking about using CXFINUNEXP as an initial condition for XGOVTDEBTBF.
12.7 Wrapping up Important Flow Variable Initializations
The preceding sub-sections focused heavily on initialization of the stock variables that, as described in the model’s own documentation, are critically important to the temporal dynamics of the equilibrating algorithms and annual flows within the social accounting matrix representation of IFs. As indicated, the interface of IFs even includes a representation of those stock variables.
Typically, however, discussion and modeling of social accounting focuses overwhelmingly or exclusively on the flows themselves; matrices generally consist of those flows at single time points, in comparative statics snap shots, or with respect to shorter-term changes in flows due to policy interventions or other drivers. IFs, too, must represent the drivers of changes in flows and the preprocessor initializes such drivers. Earlier text has attempted to explain the initialization of all of them. There are, however, a few remaining initializations prior to saving preprocessor results for use in the model.
12.7.1 Adjustment to tax rates
The discussion of tax rates in the SAM elaboration of government revenues pointed out that there would be some return to one subset of those drivers, namely the tax rates, after elaborating the asset/liability stocks. Specifically, the code around government revenues filled in initial conditions for CFirmTaxR, CSSWelTaxR, CIndirectTaxR, and CTarrifTaxR.
But it is only in the specification of stock values for inward and outward foreign direct and portfolio investment that a recent average is computed for the annual flows of FDI and portfolio investment as a percentage of GDP. The preprocessor assumes that those flows affect the value of firm income, in particular, and therefore waits until after their calculation to compute the final tax rates for CFirmTaxR, recomputing as necessary CIndirectTaxR, CTDariffTaxRSec (by sector), CHHTaxRUnskilled and CHHTaxRSkilled so that the total of government revenues as a percentage of GDP is unchanged.
[Return to this: Tariff rates receive extra attention at this point. [influenced by dyadic; discuss with José how dyadic accessed/turned on in ProcessEconomicData
12.7.2 Economic growth rates
After attention to reworking of government revenue rates, there is a call to FillInitialGDPGRNIDIM to wrap up an assortment of remaining initializations. The first of those is a computation of an initial GDP growth rate (CIGDPR) that is used in the model proper to represent each country’s basic growth rate propensity as evidenced by that of recent years and the IMF forecasts of likely growth in the coning few years. Among other contributions to the economic forecasting of IFs, that value helps identify the rate of progress in multifactor productivity. The preprocessor looks to SeriesGDP2011 (or an update as new currency base years are introduced) for the historical values and IMF forecasts. The exact period across which CIGDPR is computed will vary depending on the final year of data in the Series file, but the computation looks across a 20-year period when data are available and weights the latest 5 years more heavily than the earlier ones. Attentive to the same datafile, the routine also uses the IMF forecasts beyond the model’s base year to compute exogenous GDP growth rates that override model computations for those years. The code also sets a core long-term real interest rate variable (CINTR) at the same level as CIGDPR.
12.7.3 Poverty rates
FillInitialGDPGRNIDIM also reads data on poverty rates and poverty gap values at daily income levels such as $1,00, $1.25, $1.90, $3.10, using these to initialize poverty rate variables at range of poverty levels (notably $1.90, $2.00, $3.10, $3.20, $5.50, and country-specific poverty lines). It also reads data on GDP per capita at PPP and the Gini coefficient of countries. In order to initialize percentages of population at all of the desired income levels in variables such as CINCOMELT32 and CPOVGAP32 it uses the poverty data available within IFs, the income distribution, the GDP per capita at PPP, the assumption of log-normal poverty distributions, and national population sizes. The logic also recognizes that data and/or calculations sometimes need reasonable adjustments to recognize the inevitability of higher poverty rates at higher daily income level thresholds.
12.7.4 Water and sanitation
Finally, FillInitialGDPGRNIDIM reads values for access to safe water and sanitation (using the 3-step ladders for each as of IFs version 7.86 and moving to the 5-step ladder in versions above 7.90).
12.8 Writing Initializations to an Output File
The near final step in the logic of DATAECON is to save all of the country-specific values of the variables computed in the preprocessor. It saves them to the EcoOutput table of IFs.mdb. In most cases it saves the contents of variable names in DataEcon that begin with the letter “C” (e.g. CINTR) to a column across countries with the variable name used in the model proper without the “C” (e.g. INTR). It is left to other elements of the preprocessor to convert the values saved in EcoOutput and other similar tables from the preprocessor routines of other models in the IFs system (e.g. AgriOutput and EducOutput) to the files used by the model proper in forecasting. Part of that conversion process accommodates the movement from the country-based data files feeding the preprocessor to the potentially region-based files processed by the model proper (even when the number of the countries in data files (now 188) is identical to the number of “regions” in the model, but not always using exactly the same country names.
12.9 Calls to Final Data Processing Routines
The very last step in DATAECON consists of calls to three routines for additional processing of key elements in the calculations of the economic model. These are:
InputOutputDataAdjuster, This important routine imposes consistency on core economic initial conditions across the economic value-based general equilibrium-seeking economic model and the two physical unit-based partial equilibrium models that feed it. It also imposes base-year consistency among the generic input-output matrices used in IFs that change with economic development, sectoral value added (CVADD), sectoral gross production (CZS), sectoral production remaining for final demand after satisfying intersectoral flow demand (PFD), sectoral household consumption (CCS), government consumption by origin sector (CGS), and investment by origin sector (CINVS). It does this by process of iterative adjustment of these variables that need consistency across them in the model’s base year and for which the model proper maintains consistency across the forecast horizon. Although values for these variables were already placed into the EcoOutput table, they are overwritten after adjustments for consistency.
RegionalInputOutputData, When the number of regions in the IFs model proper is less than the number of countries in the database used by the preprocessor because model regions are aggregates of data-based countries (as in legacy IFs versions, but not in those of recent years), this routine aggregates the IO matrices of the countries in the regions with a weighted average of matrix values.
ComputeLaborFunctionsCountry. Uses GTAP data to build functions that relate national GDP per capita at PPP to labor demand propensity by economic sector.
12.10 Notes on Unemployment Data
Unemployment is an important variable within the labor market representation of economic modeling. Data on it (from the ILO via the WDI) are not always easy to understand. The following information on unemployment data is copied verbatim from the World Development Indicators website at https://databank.worldbank.org/metadataglossary/world-development-indicators/series/SL.UEM.TOTL.NE.ZS
Development Relevance: Paradoxically, low unemployment rates can disguise substantial poverty in a country, while high unemployment rates can occur in countries with a high level of economic development and low rates of poverty. In countries without unemployment or welfare benefits people eke out a living in vulnerable employment. In countries with well-developed safety nets workers can afford to wait for suitable or desirable jobs. But high and sustained unemployment indicates serious inefficiencies in resource allocation. Youth unemployment is an important policy issue for many economies. Young men and women today face increasing uncertainty in their hopes of undergoing a satisfactory transition in the labour market, and this uncertainty and disillusionment can, in turn, have damaging effects on individuals, communities, economies and society at large. Unemployed or underemployed youth are less able to contribute effectively to national development and have fewer opportunities to exercise their rights as citizens. They have less to spend as consumers, less to invest as savers and often have no "voice" to bring about change in their lives and communities. Widespread youth unemployment and underemployment also prevents companies and countries from innovating and developing competitive advantages based on human capital investment, thus undermining future prospects. Unemployment is a key measure to monitor whether a country is on track to achieve the Sustainable Development Goal of promoting sustained, inclusive and sustainable economic growth, full and productive employment and decent work for all. [SDG Indicator 8.5.2]
General Comments: Data up to 2016 are estimates while data from 2017 are projections. National estimates are also available in the WDI database. Caution should be used when comparing ILO estimates with national estimates.
Limitations and Exceptions: The criteria for people considered to be seeking work, and the treatment of people temporarily laid off or seeking work for the first time, vary across countries. In many cases it is especially difficult to measure employment and unemployment in agriculture. The timing of a survey can maximize the effects of seasonal unemployment in agriculture. And informal sector employment is difficult to quantify where informal activities are not tracked. There may be also persons not currently in the labour market who want to work but do not actively "seek" work because they view job opportunities as limited, or because they have restricted labour mobility, or face discrimination, or structural, social or cultural barriers. The exclusion of people who want to work but are not seeking work (often called the "hidden unemployed" or "discouraged workers") is a criterion that will affect the unemployment count of both women and men. However, women tend to be excluded from the count for various reasons. Women suffer more from discrimination and from structural, social, and cultural barriers that impede them from seeking work. Also, women are often responsible for the care of children and the elderly and for household affairs. They may not be available for work during the short reference period, as they need to make arrangements before starting work. Further, women are considered to be employed when they are working part-time or in temporary jobs, despite the instability of these jobs or their active search for more secure employment.
Periodicity: Annual
Statistical Concept and Methodology: The standard definition of unemployed persons is those individuals without work, seeking work in a recent past period, and currently available for work, including people who have lost their jobs or who have voluntarily left work. Persons who did not look for work but have an arrangements for a future job are also counted as unemployed. Some unemployment is unavoidable. At any time some workers are temporarily unemployed between jobs as employers look for the right workers and workers search for better jobs. It is the labour force or the economically active portion of the population that serves as the base for this indicator, not the total population. The series is part of the ILO estimates and is harmonized to ensure comparability across countries and over time by accounting for differences in data source, scope of coverage, methodology, and other country-specific factors. The estimates are based mainly on nationally representative labor force surveys, with other sources (population censuses and nationally reported estimates) used only when no survey data are available.
12.11 Mapping GTAP Economic Sectors to IFs Sectors
Although IFs theoretically can represent many more than the six economic sectors that have been represented in IFs versions for many years, it is unlikely that it will ever represent all of the sectors that are in the economic data from the Global Trade and Analysis Project (GTAP) from which a great many series are taken (not least the input-output matrices). The table below shows the mapping of the GTAP sectors to those of IFs.
| IFsSector | GTAP | |
| Abbr | SectorName | |
| Agriculture | pdr | Paddy Rice |
| wht | Wheat | |
| gro | Other Grains | |
| v_f | Vegetables, Fruits | |
| osd | Oil Seeds | |
| c_b | Cane & Beet | |
| pfb | Plant Fibres | |
| ocr | Other Crops | |
| ctl | Cattle | |
| oap | Other Anim Prod | |
| rmk | Raw Milk | |
| wol | Wool | |
| frs | Forestry | |
| fsh | Fishing | |
| cmt | Cattle Meat | |
| omt | Other Meat | |
| vol | Vegetable Oils | |
| mil | Milk | |
| pcr | Processed Rice | |
| sgr | Sugar | |
| ofd | Other Food | |
| Energy | coa | Coal |
| oil | Oil | |
| gas | Gas | |
| ely | Electricity | |
| gdt | Gas Distribution | |
| Material and Mining | omn | Other Mining |
| nmm | Non-Metallic Minerals | |
| I_s | Iron & Steel | |
| nfm | Non-Ferrous Metals | |
| fmp | Fabricated Metal Products | |
| Service | trd | Trade |
| otp | Other Transport | |
| wtp | Water Transport | |
| atp | Air Transport | |
| ofi | Other Financial Intermediation | |
| isr | Insurance | |
| obs | Other Business Services | |
| ros | Rec & Other Services | |
| osg | Other Services (Govt) | |
| dwe | Dwellings (Ownership) | |
| ICT | ele | Electronic Equipment |
| cmn | Communications | |
| Manufacture | b_t | Bev and Tobacco |
| tex | Textiles | |
| wap | Wearing Apparel | |
| lea | Leather | |
| lum | Lumber | |
| ppp | Paper & Products | |
| p_c | Petroleum and Coke | |
| crp | Chem & Rubber Products | |
| mvh | Motor Vehicles | |
| otn | Other Transport Equipment | |
| ome | Other Machinery and Equipment | |
| omf | Other Manufacturing | |
| wtr | Water | |
| cns | Construction | |
The 65 GTAP sectors also have a concordance with the Central Product Classification of the United Nations Department of Economic and Social Affairs (see that classification at https://unstats.un.org/unsd/classifications/unsdclassifications/cpcv21.pdf) and UNESA’s International Standard Industrial Classification of All Economic Activities (ISIC) at https://unstats.un.org/unsd/publication/seriesm/seriesm_4rev4e.pdf. The concordance of GTAP with those other classifications can be seen at https://www.gtap.agecon.purdue.edu/databases/contribute/concordinfo.asp. Understanding of these concordances is important also for analysis of trade data brought into IFs.
12.12 Mapping GTAP Skill Categories to IFs Labor and Household Categories
Similarly, it is important to know the mapping of the GTAP skill categories to those in IFs and useful to understand the mapping of ISCO groupings to GTAP and IFs.
| IFs Skill Category | ISCO-88 Major Group | Abbreviated name used in GTAP | Short Name | Description |
| Skilled | 1,2 | off_mgr_pros | Officials and Mangers | legislators, senior officials and managers (Major Groups 1), and professionals (Major Group 2) |
| 3 | tech_aspros | Technicians | technicians and associate professionals | |
| Unskilled | 4 | Clerks | Clerks | Clerks |
| 5 | service_shop | Service/Shop workers | service workers and shop and market sales workers | |
| 6,7,8.9 | ag_othlowsk | Agricultural and Unskilled | skilled agricultural and fishery workers (Major Group 6), craft and related trade workers (Major Group 7), plant and machine operators and assemblers (Major Group 8), and elementary occupations (Major Group 9) |
(GTAP and ISCO information copied from Walmsley and Carrico, 2013)
12.13 Bilateral Trade Data Sources and Initialization
12.13.1 Trade data sources
Our trade data are collected from two sources, CEPII’s BACI and the United Nation’s Comtrade. BACI is used to create our sectoral trade series for commodities and Comtrade is used to create our services trade series (as BACI does not yet include services). As BACI is derived from Comtrade, the integration of these two series is relatively straight forward. The subsections below also identify some other trade data series that have been useful for comparative purposes.
Tariff data comes from the World Bank’s World Integrated Trade Solution (WITS), which provide bilateral tariff revenue by country-pair at the commodity level.
The Trade Complementarity Index, measuring the degree of alignment between one country’s exports and another country’s imports, is calculated for IFs goods sectors’ data (yet to implement for services) from BACI using the World Bank methodology explained below.
12.13.1.1 CEPII BACI
Guillaume Gaulier, Soledad Zignago. BACI: International Trade Database at the Product-Level. The 1994-2007 Version. CEPII Working Paper, N°2010-23, October 2010.
Original procedures have been developed to reconcile data reported by almost 150 countries to the United Nations Statistics Division. First, as import values are reported CIF (cost, insurance and freight) while exports are reported FOB (free on board), CIF costs are estimated and removed from imports values to compute FOB import values. Second, the reliability of country reporting is assessed based on the reporting distances among partners. These reporting qualities are used as weights in the reconciliation of each bilateral trade flow twice reported. Taking advantage of this double information on each flow, we end up with a large coverage of countries not reporting at a given level of the product classification.
The dataset natively gives information about the value of trade (v, in thousands of US dollars) and the quantity (q, in tons). Individual trade flows are identified by the exporter (i), the importer (j), the product category (hs6) and the year (t). BACI is available with versions 1992, 1996 and 2002 of the Harmonized System (HS) with 6-digit disaggregation. We utilize these HS6 codes to construct our sectoral trade series by aggregating up into GTAP segments and then to IFs sectors.
12.13.1.2 UN Comtrade
UN Department of Economic and Social Affairs. 2014 International Trade Statistics Yearbook: Volume II. New York, 2015
The UN Comtrade is the largest depository of international trade data. It contains well over 1.7 billion data records for 45 years and is available on the internet!
All commodity values are converted from national currency into US dollars using exchange rates supplied by the reporter countries or derived from monthly market rates and volume of trade. Quantities, when provided with the reporter country data and when possible, are converted into metric units. Commodities are reported in the current classification and revision (HS2002 in most cases) and are converted all the way down to the earliest classification SITC revision 1. Therefore, if data is received in HS 2002 version, it is converted to HS1996, HS1988, SITC rev. 3, SITC rev. 2, SITC rev. 1 and BEC.
Time series of data for reporter countries starts as far back as 1962 and goes up to the most recent completed year. Current data is published annually in the International Trade Statistics Yearbook and can be purchased through the UN Sales Department.
The UNSD holds the copyright to Comtrade data. All rights reserved. Users cannot disseminate Comtrade raw data without the express permission of the UNSD.
12.13.1.3 UN Comrade (Services)
UN, European Commission, IMF, OECD, UNCTAD, and WTO (2010). The Manual on Statistics of International Trade in Services. New York: United Nations. http://unstats.un.org/unsd/servicetrade/default.aspx
In 2003 the Inter-agency Task Force on Statistics of International Trade in Services (TFSITS) agreed that as a part of the implementation plan of the Manual on Statistics of International Trade in Services (MSITS) the United Nations Statistics Division (UNSD), using its experience with the trade statistics database (UN Comtrade) would create a database system which will be able to process, store and disseminate statistics of international trade in services in accordance with the MSITS, including trade by service category and partner country (see Report of the Inter-agency Task Force on Statistics of International Trade in Services to the UN Statistical Commission, issued as background document of the Statistical Commission 2004). This pilot version of the UN International Trade in Services database is now publicly available via the UN Comtrade website.
12.13.1.4 IMF Direction of Trade Statistics (DOTS)
International Monetary Fund. 2015. Direction of Trade Statistics, 2015. Online: http://www.imfbookstore.org/
The Direction of Trade Statistics (DOTS) from IMF presents current figures on the value of merchandise exports and imports disaggregated according to a country's primary trading partners. Area and world aggregates are included in the display of trade flows between major areas of the world. Reported data is supplemented by estimates whenever such data is not available or current. Imports are reported on a cost insurance and freight (CIF) basis and exports are reported on a free on board (FOB) basis apart from a few countries for which imports are also available FOB. Time series data includes estimates derived from reports of partner countries for non-reporting and slow-reporting countries.
12.13.1.5 CEPII TRADEHIST
Michel Fouquin, Jules Hugot. Two Centuries of Bilateral Trade and Gravity Data: 1827-2014. CEPII Working Paper, N°2016-14, May 2016
This dataset has been built in order to analyze in historical perspective, using gravity equations, the globalization process through bilateral International trade data (see Fouquin and Hugot Working paper n°2016-13, Mai 2016). The data set gathers five types of variables: i) bilateral nominal trade flows, ii) country level aggregate nominal exports and imports, iii) nominal GDPs, iv) exchange rates, and v) bilateral factors that are known to favor or hamper trade, including geographical distance, common borders, colonial and linguistic links, as well as bilateral tariffs. We then use this dataset in order to estimate the evolution of trade costs over two centuries. Overall, the dataset we gather is unique in its temporal as well as geographical coverage: we gather more than 1.9 million bilateral trade observations for the 188 years from 1827 to 2014. We also provide about 42,000 observations on aggregate trade, and about 14,000 observations on GDPs and exchange rates respectively.
12.13.1.6 Global Trade Analysis Project (GTAP)
Aguiar, Angel, Badri Narayanan, & Robert McDougall. "An Overview of the GTAP 9 Data Base." Journal of Global Economic Analysis 1, no. 1 (June 3,2016): 181-208.
The centerpiece of the Global Trade Analysis Project is the GTAP Data Base, a fully documented, publicly available global data base which contains complete bilateral trade information (from 1995 to 2013), transport, and protection linkages. The GTAP Data Base represents the world economy and is utilized by thousands worldwide as a key input into contemporary applied general equilibrium (AGE) analysis of global economic issues. The current release, the GTAP 9 Data Base, features 2004, 2007 and 2011 reference years as well as 140 regions for all 57 GTAP commodities.
12.13.1.7 World Bank Trade in Services Database
Francois and Pindyuk (2013). Consolidated Data on International Trade in Services v8.9. IIDE discussion paper 20130101. http://data.worldbank.org/data-catalog/trade-in-services
The Trade in Services Database provides information on annual bilateral services trade flows in Mode 1 (cross-border trade) and Mode 2 (consumption abroad) for 199 countries across a multitude of sectors and years spanning 1985 and 2011. The collection of data on cross-border trade in services is notoriously difficult, in large part due to the intangible nature of services but also the high capacity needed to record such data. This is particularly true for developing countries. This database tries to fill this gap by consolidating multiple sources of bilateral trade data in services using mirror techniques, including the OECD, Eurostat, UN and IMF, as to provide a broader coverage of developed and developing countries over time. Mirror-technique is a method to retrieve export trade flows of a reporter by using information on imports of the partner country.
12.13.2 Dyadic files and structure
12.13.1.1 Adding dyadic files to IFs
The Diplometrics project has collected or created a number of series measuring bilateral influence and interaction from a number of sources. The system we implement to store, import, and access bilateral trade data is generalizable to all dyadic data with little effort. Due to concerns over the size of the files and the runtime of the model when forecasting bilateral interactions, we do not at present include the dyadic historical series nor the files needed for bilateral forecasts in the packaged version of IFs. Users that wish to access it must instead download it from our FTP site ([./Ftp://www.ifs.du.edu/BilateralInteractionData/ ftp://www.ifs.du.edu/BilateralInteractionData/]). Upon downloading the requisite files, the user must then unzip the package and place them inside the DATA folder of their IFs install (they cannot simultaneously be in the DATA/BILATERAL folder).
The files included in this additional download are DataDictDyadic, DataDictDyadicForecast, IFsForDyadic, and IFsHistSeriesDyadic. All four files are necessary for the proper functioning of the dyadic display and bilateral forecasts. DataDictDyadic and IFsHistSeriesDyadic hold the metadata and historical series, respectively, for the bilateral variables. The other files included in the download (DataDictDyadicForecast and IFsForDyadic) are utilized in the background by IFs when creating bilateral forecasts. Unlike with the historical series located in IFsHistSeriesDyadic and described in DataDictDyadic, dyadic forecast variables and scenario parameters are found in IFsVar.
12.13.1.2 File Structure
The structure of DataDictDyadic is the same as DataDict, and the structure of IFsHistSeriesDyadic resembles the IFsHistSeries. While the tables in the IFsHistSeries takes the form of:
Country, FIPS_Code, Year1, Year2, …, YearN, Earliest, MostRecent
The layout of tables in IFsHistSeriesDyadic have the following form:
Actor, Actor_FIPS, Partner, Partner_FIPS, Year1, Year2, … , YearN, Earliest, MostRecent
12.13.3 Preprocessor initialization of bilateral data
Before the model can be run to produce forecasts, base year values must be set for dyadic trade in each sector among all the countries in IFs. This process draws upon raw historical data for the base year (or most recent year of data) from both bilateral and country-level sources, as well as estimations from the gravity model.
Null (missing) bilateral trade data are filled by distributing the difference in trade volume between dyadic and monadic source using the gravity model. Even after this process, country sums of bilateral exports and imports will often not match monadic estimates, and so undergo a normalization process to enforce consistency between the bilateral and country-level trade models. All of this is done in the model’s data preprocessor, greatly facilitating handling data updates and even base year changes. The multiple requirements lead, however, to a fairly complex base year data initialization process with several steps defined algorithmically and sometimes involving iteration. This process is explained in greater detail below.
Due to the enormous number of datapoints covered in a bilateral trade dataset (which often include not just total directed trade flows between countries, but data representing the flows across hundreds of commodities), data providers often remove entries where flows are zero. This introduces a significant challenge in distinguishing between missing data and true zero flows. Luckily CEPII provides a dataset which lists all true-zero flows.
The first step in the preprocessor’s initialization of bilateral trade is to combine the bilateral trade data with the zeros-data. This results in a trade flows matrix with entries that contain zero, non-zero, and null values of trade between all 188 countries. We also construct a matrix populated with gravity-based estimates and overwrite values with the same zeros data, resulting in a complete (no missing values) gravity-flows matrix. We construct an additional two shares matrices by normalizing our trade and gravity matrices such that all rows sum to 1.
Due to missing or misreported data, row or column sums of our trade-flows matrix do not match country-level estimates of trade (exports and imports) by sector. We estimate this difference by subtracting the row-sum of the trade-flows matrix (the sum of exports from a country to all other countries) from our values of XS which has already been estimated by the Preprocessor. We save this result in a vector (XSAdjVal). We divide this value by XS to calculate the share of total country exports not accounted for in the bilateral data and save the result in a separate vector (XSAdjShr).
While country-aggregates of exports are generally lower than country-level estimates derived from balance of payments data, there are some countries where the opposite is true. In these instances, we adjust all (non-zero, non-null) bilateral exports downwards by distributing the negative residual (XSAdjVal) according to the trade-shares values.
For the majority of cases, we first use the positive residual (XSAdjVal) to fill null values, and then (if appropriate) to augment all (non-zero) bilateral exports. To achieve this, for each exporter, we sum the gravity-shares values whose index matches a null value in the trade-flows matrix. For example, if Country J has missing export data for Country R and Country S, we sum the gravity-shares values for elements J,R and J,S. These values are saved in an internal vector (NullShare).
For the last step in filling holes we consider two country cases. First, are the countries where a country’s NullShare value is greater than its residual share (XSAdjShr). This corresponds to cases where the gravity-estimated shares of the missing flows (flows from J to R and J to S in the above example) are expected to account for the entirety of the unallocated flows (XSAdjVal). In this case, we allocate the residual exports (XSAdjVal) to the missing elements in proportion to their corresponding gravity-shares values, and update these values in the trade-flows matrix.
For the second case, where the elements with missing flows are not expected to fully account for unallocated flows (NullShr < XSAdjShr), we calculate the null values’ share of the unallocated flows as the product of XSAdjShr and NullShare. We then distribute this value across the missing values in the trade flows matrix proportional to their respective gravity-shares values. At this point, the country has no null elements in their row, but still some unallocated flows. To account for this remainder, we reestimate a trade-shares row vector (dividing each row element by the row sum) and distribute the remaining flows proportionally.
The above procedure results in a trade flows matrix where all row-sums are equal to XS. To ensure that the column-sum of this flows matrix is equal to MS, we enter into an balancing process that iteratively adjusts row and column values until their sums are equal to (within a small tolerance) XS and MS.[17]
12.13.4 Dyadic displays
The IFs system facilitates analysis of dyadic/bilateral data and forecasts with two displays. Because dyadic analysis within IFs began with analysis of historical data, both displays are found under the Data Analysis main menu option rather than under the Display option in spite of the fact that the second of them allows analysis of both data and forecasts. These are named Bilateral Interaction Display and Bilateral Interaction Display with Gravity Option. The first is available regardless of whether the bilateral switch bilateralsw parameter is activated and the bilateral base case has been created, but the second is only available when that parameter has been set to 1.0 in a model run. The text of economic model documentation on Bilateral Elaboration of Trade and Other Interstate Flows explains the general process of setting up bilateral elaborations of the IFs economic model. Here we discuss the two displays in turn.
12.13.4.1 Bilateral interaction display
The Bilateral Interaction Display of IFs (under the Data Analysis option in the Main Menu) currently displays historical dyadic data for 13 series (using series from IFs.mdb/GovConflictDataDict and GovConflict files). The display could be expanded to include additional series, but has several limitations, including with respect to: (1) selecting multiple dyad-pairs in either the line or table displays, (2) selecting multiple actors or multiple partners with any of the displays, and (3) drawing cross-sectional graphs. This is in many respects a legacy display form and almost all users will prefer using the form for Bilateral Interaction Display with Gravity Option.
12.13.4.2 Bilateral interaction display with gravity option
The form for Bilateral Interaction Display with Gravity Option is also under the Data Analysis option in the Main Menu. It is available only when the bilateral data files have been added to an install version of IFs, the bilateralsw parameter has activated, and the Base Case of the model has been rebuilt and run. Moreover, the form is password protected and requires supply of this password: dyad4IFs12. The form facilitates analysis of both historical data and forecasts.
This bilateral display has many features that make it very useful. These include:
- Selecting series from a very large set of the monadic historical series in IFs that have been identified as having some relationship to the dyadic forecasts.
- Selecting across the entire set of dyadic forecast variables of IFs for display of actor-target interaction within pairs of individual countries, for individual countries in interaction with groupings of them, or for groupings in interaction with other groupings.
- Combining forecasts of dyadic variables with historical analog data series.
12.14 Labor Data[18]
Labor supply and unemployment data that we use in our model is from International Labor Organization (ILO). For data on the demand side, we used data from the Global Trade Analysis Project. Wage variable used in the equilibration algorithm is an index anchored to the base year of the model.[19] IFs preprocessor prepared these data for model use using various estimation, conversion and reconciliation processes.
12.14.1 Definitional Issues
There are ambiguities in the way some of the labor market variables are defined. Labor participation rates and the rate of unemployment are two that need special attention.
The size of the labor supply available for economic activities is expressed with the labor force participation rate. ILO defines this as a ‘measure of the proportion of country’s working-age population that engages actively in the labor market, either by working or looking for work.’[20]National labor force surveys and census data are used to estimate this rate. The definition of labor force here includes both employed and unemployed and the rate is expressed as a percentage of working-age population. Working-age population is defined here as the population above legal working-age. For international comparability, ILO adopts a convenient minimum threshold of fifteen years as working age and avoids putting any upper age limit. In practice, both the minimum and the upper-age limits can vary by country. For example, the working-age in the USA begins at sixteen years. In the Netherlands the upper age limit is seventy-five years, whereas South African data uses an upper age limit of 64.[21]
Ambiguities are more abundant in the definition of unemployment. ILO came up with a guideline on this as well. Per the ILO guideline, the unemployed are those among the working-age population who are not employed, are available for work, and are actively looking for jobs[22]; the unemployment rate is expressed as a percentage of those who are in the labor force. The availability and job-seeker status could be defined in different ways giving rise to incompatibility in data. While there seems not be much room for disagreement on whether someone is at work or not, whether that work should be considered as employment can often be contested.
The debates around the nature and type of employment can range from gainfulness to workplace setting. For example, many workers in the low-income low-regulation developing countries work outside the purview of formal enterprises. According to an ILO estimate, more than half of the global labor force and more than 90% of Micro and Small Enterprises (MSEs) worldwide are in the so-called informal economy.[23] This might explain the apparently counterintuitive pattern of low unemployment rate in some low-income countries (e.g., 2.2% for Guatemala) and relatively higher numbers for some of the developed nations. The low numbers in the poorer countries hide the prevalence of extremely low wage jobs in the informal sectors in these countries, the only options for the vulnerable people in the absence of any kind of social safety net. Also, in the developed countries the so called ‘gig-economy’ is attracting more and more workers who choose to work on their own rather than in a formal enterprise. ILO conceptualization makes the informal work part of total employment. The stacked Venn diagram below presents the relationship among the labor force metric including informal employment. IFs also models informal economy both in terms of GDP share and employment share of informal in the total economy and employment.
Incompatibility can arise in the treatment of various population groups for the computation of the denominator for participation and unemployment rates.[24] ILO makes their best efforts to make adjustments in the data for the sake of international comparison. For example, ILO asks countries that deviate from ILO guidelines to collect data needed to convert national figures to ILO figures. It is likely that some differences might have slipped past the adjustment process. We use ILO data and continue to update our database from ILO on a regular basis.
The GTAP data that we use for the demand side of the labor model is taken as labor headcounts. It appears[25] that the data include both formal and informal employment. We also need mention here that the GTAP database reconciles the labor data to calibrate the general equilibrium modeling that they do for the trade analyses. The data could thus be somewhat different from data collected through direct surveys. IFs being a CGE model itself benefits from using calibrated data.
12.14.2 Sources of labor data
IFs model uses ILO data for labor participation rates and for the unemployment rate. The data in IFs are collected from World Bank’s World Development Indicators (WDI) database. According to their documentation, WDI obtained the data from the ILO.
Unemployment rate data in IFs is also collected from WDI. Like the participation rates WDI also obtains their unemployment data from ILO.[26]
For employment and labor demand data IFs use Purdue University’s Global Trade Analysis Project (GTAP) database. GTAP collects and compiles factor payments, import, and intersectoral flow data to calibrate CGE models of national economies for trade and other analyses. In their ninth release in 2016, GTAP published data for 140 countries and regions for the year 2011. The earlier GTAP releases, which IFs model used for its previous versions, compiled data for the years 2004 and 2007. GTAP data release aggregates economic activities into 57 commodities and activities following International Standard Industrial Classification (ISIC). IFs model maps the 57 GTAP sectors into six economic sectors of IFs – agriculture, energy, material and mining, manufacture, services and ICT. Appendix 2 presents two tables listing the sectors mappings between IFs and GTAP, and GTAP and ISIC. GTAP further disaggregates labor in each of the commodities/activities into five occupation and skill categories following the nine category International Standard Classification of Occupations (ISCO-88). The IFs model collapses five GTAP occupation categories into the simple IFs dichotomy of skilled and unskilled. The mapping of occupations and skills are presented in the third appendix of this document.
The data in the main GTAP database, prepared for CGE modeling, are all in dollar units and do not thus include labor headcounts. We have used a ‘satellite’ GTAP database[27] for labor headcounts by skill and sector. The labor counts were also used to plot labor requirement functions for each of the IFs economic sectors and skill categories. The wage share of skilled and unskilled labor in each sector was computed using the labor headcounts and labor payments.
12.14.3 Scope of IFs labor model
IFs labor model simulates labor market at the national level. Each national labor market forecasts labor demand and employment by six sectors - agriculture, energy, mining, manufacture, services and ICT- and two skill levels - skilled and unskilled. The supply side does not have sectoral representation. IFs forecasts total labor force and labor supply by the two skill levels. Labor participation rate is computed in IFs by gender. Wage and unemployment rate are forecast for the overall labor market only.
12.14.4 Labor model preprocessor
IFs system has a data preprocessor that prepares the initial conditions for the model using historical databases and various assumptions and estimated relationships to fill in the missing data and make data adjustments as needed.[28] Pre-processing of labor data takes place in two IFs pre-processing modules. Labor participation rate data, which is closely related to demography, is processed in the population preprocessor. Unemployment rate and labor demand data are processed in the economic preprocessor.
12.14.4.1 Preprocessing labor participation rate and unemployment
For initializing labor participation rates by sex (LABPARR) the model uses the historical values from the base year or the most recent year with data.[29] For countries with no data we use regression relationships of the participation rates, for men and for women, with income per capita. The relationships, shown in the next figure, are not great. However, the functions affect only five countries for which we do not have any data at all: Grenada, Kosovo, Micronesia, Seychelles and South Sudan.[30]
IFs data series SeriesLaborUnemploy% is used for the initialization of unemployment rates. That series has annual unemployment rates for one or more years between 1980 and 2016, for 181 of the 186 IFs countries. For five countries (Grenada, Kosovo, Micronesia, Taiwan and South Sudan[31]) there is no data at all. To fill in the missing data we use a regression function of unemployment rate against GDP per capita. Like the participation rate functions, this function does also not have much of an explanatory power.
12.14.4.2 Preprocessing labor demands and employment from GTAP
The IFs economic preprocessor reads labor headcount and labor payment data from the GTAP database. In addition to performing sector and occupation/skill mapping between GTAP and IFs, preprocessor also use the labor headcount data to compute labor coefficient functions, the principal driver of labor demand in the IFs model.
Labor coefficients are defined as the amount of labor needed to produce one unit of value added in a certain sector of the economy. The coefficients depend on the level of technology. The model uses GDP per capita as an indicator of the level of technological development. IFs preprocessor estimates labor coefficient functions for labor of different skill levels for the different sectors of the economy.
The functions are derived from GTAP data we described earlier. The model preprocessor reads data on factor payments and aggregates data from 57 GTAP sectors to six IFs sectors. Shares of payment going to skilled and less-skilled workers in each of the sectors are then computed. Countries are grouped according to their level of technological development as represented by per capita income. For each group labor coefficients are obtained by taking an average of the country coefficients. We also convert labor payments data to labor headcount data using per capita income as a proxy for average wage. Labor coefficients and income are then plotted into a power function relationship. The figure below plots some of those labor functions. The functions fit quite well with a power law formulation.[32]
12.15 Poverty by Age and Sex
The above descriptions overwhelmingly address the processing that occurs in RecomputeEconomicOutput. After all of the processing in the that routine is complete, DataEcon calls RecomputePovertyOutput. The purpose of that routine is to read initial conditions for poverty by age and sex, with the age categories determined in a project that the Pardee Center undertook with UN Women and most of the data for that representation coming from that organization.
12.16 Bilateral Data Processing
When the preprocessor is called from the IFs menu option of Extended Features/Rebuild Model Base, the screen that appears on which to select the time horizon for the rebuild provides an option for “Using Bilateral Data.” When that option is selected, files of bilateral data are copied to a subfolder of the Data folder within IFs. And when data is done, the routines RecomputeEcDyadicOutput and RedetermineEcDyadicBase and called. Those routines process all the bilateral data and initialize variables that the IFs model proper will use to add bilateral international flows and analysis, mostly in elaboration of the monadic forecasting on which this document has primarily focused.
- ↑ For data on participation rates by age in the U.S. as tracked by the Bureau of Labor Statistics see https://www.bls.gov/emp/tables/civilian-labor-force-participation-rate.htm
- ↑ In the 2017 base year model runs of IFs Version 7.95 there were 46 countries in the database with unemployment rates at higher than ten percent.
- ↑ For reasons explained in the conceptual sections, the adjustment factor in the demand side is stronger than that in the supply side.
- ↑ We collapse GTAP’s 57 sectors into the six economic sectors of IFs. GTAP collapses the nine occupation categories of ISCO-88 into five. In IFs those five categories are collapsed into a binary – skilled and unskilled. The sectoral and skill mappings are described in two appendices of these document.
- ↑ David K. Bohl took a lead role in much of the Pardee Center work on representation of the informal economy. Mohammod T. Irfan, Eli Margolese-Malin, José R. Solórzano, and Barry B. Hughes were also actively involved.
- ↑ In recent releases of GTAP data, the project has expanded the classes of household labor categories. Walmsley and Carrico (2013) identify them as five: Officials and Managers, Technicians, Clerks, Service/Shop Workers, and Agriculture and Unskilled. Given the challenges of consistent data gathering for the expanded set, Dominique van der Mensbrugghe, the Director of GTAP, recommended against early reformulation to take advantage of it.
- ↑ Mohammod Irfan has taken the lead role in the IFs system’s modeling and forecasting of poverty.
- ↑ In a poster presentation at the 2021 conference of the Integrated Assessment Modeling Consortium, Kanisha Narayan, Brian O’Neill, Claudia Tobaldi and Stephanie Waldhoff found that using principal components analysis in projecting net income deciles improved (raised) projections of the 10th (highest income) decile relative to relying on a log-normal approach.
- ↑ https://blogs.worldbank.org/opendata/monitoring-poverty-us320-and-us550-lines-differences-and-similarities-extreme-poverty
- ↑ For data provider protection against unauthorized use, original data on age-sex poverty rates collected for 89 countries were aggregated to 6 regions. Data on the sex-poverty difference by age were also provided for 30 countries. Using regional aggregates, country-level sex-poverty difference values, and demographic data, UN Women produced age-sex poverty rate estimates for these 30 countries. Because the geographic regions provided do not neatly overlap with income or demographic categories, hole filling for unrepresented countries currently use a global average.
- ↑ For more information on scenario development see: https://pardee.du.edu/wiki/Guide_to_Scenario_Analysis_in_International_Futures_(IFs)
- ↑ GTAP database helped us compute wage rates by sector and skill.
- ↑ For elaboration of all balance of payments components including these see the IMF’s Balance of Payments and International Investment Position Manual at https://www.imf.org/external/pubs/ft/bop/2007/pdf/bpm6.pdf. For a good simplified summary see https://www.rba.gov.au/education/resources/explainers/the-balance-of-payments.html
- ↑ See https://en.wikipedia.org/wiki/Net_foreign_assets and https://en.wikipedia.org/wiki/Net_international_investment_position for simple descriptions. See https://data.imf.org/regular.aspx?key=62805744 for tables by country and https://data.imf.org/regular.aspx?key=62805745 for tables by varialble.
- ↑ https://en.wikipedia.org/wiki/Net_international_investment_position
- ↑ The IMF Balance of Payments and International Investment Position Manual – Sixth Edition BPM6 (p. 230-231) notes that in case of unsustainable current account deficit, depreciation of exchange rate is one adjustment mechanism.
- ↑ While this process ensures consistency between the dyadic and monadic trade models, it potentially introduce some issues. First, it explicitly privileges monadic estimates (based largely from World Bank balance of payments statistics) over Comtrade-based estimates. Second, it runs the risk of inflating trade values between well documented partners. Third, it may initialize trade between partners where there are in fact zero-flows.
- ↑ Mohammod Irfan took the lead in building the labor model, including identifying the available data series for it and structuring the preprocessing of them. This section also draws heavily on text he has written to document it.
- ↑ GTAP database helped us compute wage rates by sector and skill.
- ↑ http://www.ilo.org/ilostat-files/Documents/description_LFPR_EN.pdf
- ↑ https://www.bls.gov/fls/flscomparelf/technical_notes.pdf
- ↑ The definitions around employed and unemployed were agreed upon by nations through the ‘Resolution concerning statistics of work, employment and labor underutilization’ adopted by the 19th International Conference of Labor Statisticians (ICLS) in 2013. (Bourmpoula et al, 2017: 6).
- ↑ http://www.ilo.org/global/topics/employment-promotion/informal-economy/lang--en/index.htm
- ↑ For example, the USA excludes people in the defense services and those in the prisons or mental asylums in their computation of the civilian non-institutional working-age population. There are also variations in the treatments of students, just laid-off and family workers. Please see https://stats.bls.gov/opub/mlr/2000/06/art1full.pdf for a discussion
- ↑ Please see the webpage for documentation on GTAP labor data statistic: https://www.gtap.agecon.purdue.edu/resources/res_display.asp?RecordID=3248
- ↑ The name of the IFs table is SeriesLaborUnemploy%
- ↑ See Weingarden and Tsigas, 2010 for the details on the preparation of this database.
- ↑ For more details, please see ‘The Data Pre-Processor of International Futures (IFs)” by Barry B. Hughes (with Mohammod Irfan) at http://www.ifs.du.edu/assets/documents/preprocessorv1_0.pdf
- ↑ The data tables that the IFs model pre-processor use for initializing labor participation rates are: SeriesLaborParRate15PlusFemale%, SeriesLaborParRate15PlusMale%.
- ↑ We should try to collect participation rate for these countries from country sources.
- ↑ These are pretty much the same countries for which we do not have any participation rate data. This indicates ILO might have some administrative limitation in reporting data for these countries (notice Kosovo, Seychelles etc in the list)
- ↑ This is interesting given the prevalence of power law in all sorts of scale-up activities (West 2017).
13 Appendix B: Block Diagrams
This section presents several block diagrams that are central to the two major components of the economics model, the goods and services market—with special emphasis on the production function— and the broader SAM. Across almost all the development of the IFs economic model and other models in the system, Barry Hughes (and some other team members) heavily used causal diagrams and block diagrams as both an aid to development and in documentation of it. The block diagrams were done in Visio software. The building and refinement of those has not continued in recent years. Therefore, the block diagrams in this appendix, albeit hopefully useful, must be understood to be to some degree a legacy feature of IFs development.
13.1 Economics Overview
The economic model represents supply, demand, and trade in each of six economic sectors: agriculture, primary energy, raw materials, manufactures, services, and information/communications technology. The model draws upon data from the Global Trade and Analysis Project (GTAP) with 57 sectors as of GTAP 8; the preprocessor collapses those into the six IFs sectors and theoretically could collapse them into a different aggregated subset.
Inventories (or stocks) are the key equilibrating variable in three negative feedback loops. As they rise, prices fall, increasing final demand (one loop), decreasing production (a second loop), and thereby in total decreasing inventories in the pursuit over time of a target value and equilibrium. Similarly, as inventories rise, capacity utilization falls, decreasing production, and restraining inventories.
Physical investment and capital stocks are the key driving variables in an important positive feedback loop. As capital rises, it increases value added and GDP, increasing final demand and further increasing investment. Similarly, government social investment can increase productivity, production and inventories in another positive feedback loop.
The figure below also shows some production detail. A-matrices, which are specified dependent on the level of development (GDP per capita), allow the computation from value added of gross production and of the production that is available, after satisfaction of intersectoral flows, for meeting final demand. It is the balance of this production for final demand with actual final demand that determines whether inventories grow or decline.
The calculation of gross production (ZS) in value terms within the economic model is overridden by calculations of physical production converted to value in the agricultural and energy models when respective switches (AGON and ENON) are thrown as in the default of the IFs Base Case scenario.
13.2 Value Added
A Cobb-Douglas production function determines value added. Thus two principal factors are capital and labor. Labor is responsive not just to population size and structure, but to the labor participation rate, including the changing role of women in the work force. Accumulated growth in the level of technology or multifactor productivity (MFP), in a "disembodied" representation (TEFF), modifies these factors. Immediate energy shortages/shocks can also affect value added.
13.3 Economic Aggregates and Indicators
Based on value added and population, it is possible to compute GDP, GDP at purchasing power parity, and a substantial number of country/region-specific and global indicators including several that show the extent of the global North/South gap.
13.4 Household Accounts
The most important drivers of household income is the size of value added and the share of that accruing to households. That share, divided further into unskilled and skilled households, is initialized with data from the Global Trade and Analysis Project and changes a function driven by GDP per capita. Household income is augmented by flows from government and firms (dividends and interest). Most of household income will be used for consumption, but shares will go back to the government via taxes and to savings.
Once the total of household consumption is known, if is divided across the sectors of IFs using Engel elasticities that recognize changing use of consumption as levels per capital rise.
13.5 Firm Accounts
Firms retain as income the portion of total value added that is not sent to households in return for labor provided. Income of firms functioning within a country (ownership in IFs is not designated as domestic or international) benefit from inflows of portfolio and foreign direct investment. Firms direct their income to governments in the form of tax payments, to households as dividends and interest, to the outside world as portfolio or foreign direct investment, and to savings (available for investment).
13.6 Government Accounts
Government revenues come from taxes levied on households and firms. The total expenditures are a sum of two sub-categories, direct consumption and transfer payments (the latter in turn being a sum of payments for pensions/retirement and welfare.
The annual government balance is the difference between revenues and expenditures and increments or decrements government debt in absolute terms and as a portion of GDP. That stock variable in turn sends back signals to both revenue and expenditure sides of the model so as to keep the debt at reasonable levels over time.
The level of government consumption and its distribution across targets are important policy-relevant variables in the model. Government consumption is spread across several target spending categories: military health, education, traditional infrastructure, other infrastructure, research and development, other/residual, and foreign aid). The distribution to most of those categories is endogenously determined by functions, but other models in the IFs system provide special signals for military, education, and traditional infrastructure spending. Demand for military spending involves action-reaction dynamics (when a switch is turned on) and threat levels. Demand for educational and infrastructure involves full models. Demands will not equal supply and all demands are normalized to the supply, but special protection can be given to the demands for education and infrastructure spending.
Educational spending by level of education (primary, secondary, and tertiary) is further broken out of total educational spending in the education model but targets can be changed via a multiplier.
13.7 Savings and Investment
Savings is a sum of the savings by households, firms, the government (its fiscal balance) and net foreign savings. Investment is most immediately a sum of gross capital formation and changes in inventories.
As in other parts of the IFs economic model, there will not be an exact equilibrium between savings and investment in any given time step. The system will chase equilibrium over time with the help of two mechanisms. The smoothed pattern of savings over time will affect investment. So, too, will interest rates that respond to changes in inventories or stocks of goods and services.
13.8 Trade
The trade algorithm of IFs relies on a pooled rather than bilateral trade approach. That is, it does not track exactly who trades with whom, maintaining instead information on gross exports and imports by sector and in total. The algorithm sums import demand and export capacity across all traders (in a given sector), defines world trade as the average of those two values, and then normalizes demand and capacity to the total of world trade to determine sectoral exports and imports by geographic unit.
World trade as a percentage of GDP (WTRADE) is also computed from the trade variables shown above.
13.9 International Finance
The current account depends on international loan repayments and foreign aid flows as well as on the trade balance. The exchange rate floats with the debt level (in turn responsive to the current account balance) and is the key equilibrating variable in two negative feedback loops that work via import demand and export capacity (see description of trade).
13.10 Labor
13.10.1 Current Structure
The diagram below shows an outline of the IFs labor model. On the supply side, the total labor pool (LAB) is computed from the labor force participation rates, by sex, (LABPARR) and the population (POP) in their working age, i.e., population over 15 (POP15TO65 + POPGT65). Participation rates are driven by the demographic changes with an additional negative impact from aging and a catch-up in female participation rate. Skill level of the labor supply (LABSUP) is driven by the level of development (GDPPCP) and
The demand for labor is driven by labor-coefficients (LABCOEFFS) computed from coefficient function representing shifts in demand with technological progress as proxied by the level of development (GDPPCP). Coefficients computed by sector and skill gives the labor requirement by skill type for each unit of value added (VADD) in the sector. Multiplying these coefficients with projected value added in each sector gives an estimate of the labor demand.
Any surplus or shortage between total labor demand and supply is used to compute the rate of unemployment. Deviations in the unemployment rate (LABUNEMPR) signal wage changes through an equilibrium seeking algorithm. Both demand and supply respond to the wage variable (LABWAGEIND) indexed to the base year. The supply responses are much slower than the demand responses.
13.10.2 Thoughts on next steps
As most of you know, I have been thinking about the interactions of our emerging labor model with two other representations already in the model, namely urbanization and the size of the informal economy. This was reinforced by the Uganda problem, when we found that the movement of agricultural labor to other sectors far exceeded the rate of migration implicit in the urbanization rate and was creating a very high GDP growth because of labor’s much higher productivity in other sectors.
The figure below reflects the current model in part, augmented by some thinking about where we might go next. I hope it can help generate conversation and progress. And please correct any errors I am making here as well as making suggestions.
Heavy lines are flows, solid lines are causal links/algorithms in the model, dashed lines are possible future linkages.
Our design must reflect data availability as well as the theoretical and empirical work of others. As I understand it, our informal labor data are only for the non-agricultural sector. And our unemployment numbers (often very low for LDCs) do not include informality. According to Mohammod, the GTAP labor data cross over both formal and informal labor.
Our historical series on urbanization are considerably longer and more complete than those on agricultural labor. The superiority of urbanization data and the fact that our projections generally avoid major transients in both initial conditions and trajectories led us recently to introduce the pattern of urbanization as a constraint on the flow of agricultural labor to other sectors (the rate of which was earlier determined only by cross-sectional functions estimated from GTAP data).
That correction substantially reduced the bubble of economic growth in Uganda. But I think we are still missing one important representation, namely the fact that much or most of the movement of agricultural labor in lower income countries is not into formal labor (where again it has pretty high productivity) but initially to informality, where we already have a representation that shows informality’s less positive impact on MFP. Further, what we have now is a model where current representation of change in informality reduces it fairly rapidly over time as things like education and governance improve and push it down. Our current model behavior tends to show transients in trajectory for developing countries between mostly pretty stable percentage size of labor informality share historically to significant decrease in the percentage that is informal in our projections. That decline in our projections should/could be slowed down by a having most or all of agricultural labor moving into informality, thereby replacing that moving to formality. On the first modeling pass I would be inclined to have all of the ag labor move first to informality and see how informality behaves in projections relative to historical patterns of its change. And I think that is consistent with the long accepted portrayal by Lewis of a huge pool of agricultural and informal labor in developing countries that tends to hold down formal sector wages until it is largely absorbed (when countries reach the (Lewis turning point”). If we keep that informal percentage share higher, its constraining effect on MFP rise will remain longer and hold down overall GDP growth in countries like Uganda for a longer period.
One thing I am struggling with is how all of this should affect our current labor model, which is basically equilibrating the total of both formal and informal labor (in one big pool across all sectors). I tend to think that, consistent with work by Fields and others in articles Mohammod has given me), we should actually think of that labor model as being for non-agricultural formal labor only, not all of labor. Many labor models apparently differentiate formal and informal in labor modeling equilibration processes and I am inclined to think that we do not really need to represent demand and supply in the informal arena or in ag, but only in formal non-agriculture. Open for discussion.
Also, we all have in mind the disruptive labor market effects of AI and I think when/if we do ultimately represent those, we should think in terms of it affecting formal non-agricultural labor demand. To be considered.
Overall, bringing together urbanization, labor migration from agriculture to other sectors, and differentiating informal and formal with labor market representation only for the latter, should help address one of the issues that long kept me from wanting to tackle building a labor market in IFs at all. I kept saying that there is no way we can realistically project unemployment in 2050 in Chad. And I still believe that. But the emerging structure is not really concerned with that, unemployment is the tail not the dog and in what I am suggesting remains the tail. The dog are these flows of labor across ag and non-ag sectors and between informality and formality. They are the dog in part because they have considerable influence on MFP and GDP growth. And they should probably ultimately be considered by us in determination of Gini. Those flows are something I do think we can meaningfully say more about in the long term across countries than we can about unemployment and which will be very important to our work on SDGs and with the UNDP and country governments.
13.11 Informality
In the IFs model, developmental drivers are represented by years of educational attainment by adults (15 years and older), which serves as a proxy for overall levels of human capital. In terms of secondary drivers, three variables in the model tend to push enterprise from the formal to informal sector, namely the nature of the business regulatory environment, the size of the tax burden, and the level of corruption. Two additional variables in IFs tend to pull informal activity toward formality, namely government to household transfers and spending on research and development.
13.12 Income Distribution
Domestic income distribution is represented by the Gini coefficient. That is calculated with a Lorenz curve that looks at the share of population and income held by the only two subgroups for which we have that information, namely unskilled and skilled households. That part of the calculation is fundamentally mechanical. The complicated part of the specification is the division of the population into unskilled and skilled labor portions and thus households. We have built formulations for that driven by the formal years of education attained by adults and the GDP per capita.
Given domestic Gini indices, it is also possible to compute global Gini indices, both treating countries as wholes (GINI) and computing across the world at the household level (GINIFULL).
13.13 Poverty
The calculation of poverty levels is fairly straightforward if one has the average level of consumption per capita (or income) and its distribution as indicated by the Gini index (and if one assumes that the distribution underlying the Gini index is log-normal). The internal calculation using those variables will, however, almost inevitably produce a rate of poverty at odds with the provided by national surveys. We therefore compute a ratio of those in the first year to allow adjustment in forecast years of the values from the lognormal calculation.
As a rough check on the values produced by lognormal calculation we also compute a value of poverty estimated from a cross-sectional function linking GDP per capita (and PPP) and Gini to rates of poverty.
13.14 Informal Economy
The IFs model represents the overall size of the informal economy in terms of the informal shares of total labor and total GDP. The model first uses several driver variables to calculate the informal labor share, broken down by sector (either the informal sector or the formal and household sector) and by sex. Years of educational attainment by adults (aged 15 and older) is used as the core or deep driver; the other drivers used represent the push and pull factors that keep or push people and businesses out of the formal sector or pull them into it. The push factors modelled are: (1) the business regulatory index, which represents the level of red tape facing businesses trying to formalize and the regulatory burden formal companies must operate under; (2) the tax rate on corporate profits; and (3) the level of corruption. The pull factors modelled are: (1) government spending on social welfare and pensions as a percent of GDP, which is used as a proxy for the general strength of government capacity and the social safety net which can keep workers from having to turn to informal means to survive; and (2) spending on research and development as a percent of GDP, which has an important and independent, though relatively weakly supported, effect on informal GDP share.
The informal labor share is then used, combined with additional drivers, to calculate the share of official GDP that is informal (we assume, based on the non-observed economy framework used by the OECD and a growing number of countries that official GDP statistics capture the size of the informal economy within it). The share of informal GDP has two direct forward linkages, (1) to multifactor productivity or total productivity, and (2) to tax revenues, with the implication that the greater the share of informal GDP, the slower official GDP grows[1] and the more constrained government revenues become. The impacts on GDP and government finances then feed forward to the rest of the IFs model, including back to the drivers of informal labor share.
The upper right of the diagram provides a basic elaboration of the forward linkages of informal GDP and of the impact of formalizing it on economic productivity and government revenues.
14 Extra Material from 2015 Version of Documentation
14.1 Dominant Relations
In any long-term economic model the supply side has particular importance. In IFs, gross domestic product (GDP) is a function of multifactor productivity (MFP), capital stocks (KS), and labor inputs (LABS), all specified for each of six sectors. This approach is sometimes called a Solowian Cobb-Douglas specification, but IFs helps the user get inside the multifactor productivity term, rather than leaving it as a totally exogenous residual.
The following key dynamics are directly related to the dominant relations:
- Multifactor productivity is a function partly of exogenous specification of an annual growth rate in it for the systemic technology leader, base rates of relative technological advance in other countries determined via an inverted U-shaped function that assumes convergence with the leader, and of an exogenously specified additive factor for control of specific regions or countries.
- Multifactor productivity is, however, largely an endogenous function of variables determined in other models of the IFs system representing the extent of human, social, physical, and knowledge capital; their influence on production involves coefficients that the user can control.
- Capital stock is a function of investment and depreciation rates. Endogenously determined investment can be influenced exogenously by a multiplier and the lifetime of capital can be changed.
- Labor supply is determined from population of appropriate age in the population model (see its dominant relations and dynamics) and endogenous labor force participation rates, influenced exogenously by the growth of female participation.
The larger economic model provides also representation of and some control over sector-specific consumption patterns; trade including protectionism levels and terms of trade; taxation levels; economic freedom levels; and financial dynamics around foreign aid, borrowing, and external debt.
14.2 Structure and Agent System
Goods and Services Market
| System/Subsystem | Goods and Services |
| Organizing Structure | Endogenously driven production function represented within a dynamic general equilibrium-seeking model |
| Stocks | Capital, labor, accumulated technology |
| Flows | Production, consumption, trade, investment |
| Key Aggregate Relationships
(illustrative, not comprehensive) |
Production function with endogenous technological change; price movements equilibrate markets over time |
| Key Agent-Class Behavior Relationships
(illustrative, not comprehensive) |
Households and work/leisure, consumption, and female participation patterns;
|
Households, firms, and the government interact via markets in goods and services. There are obvious stock and flow components of markets that are desirable and infrequently changed in model representation. Perhaps the most important key aggregate relationship is the production function. Although the firm is an implicit agent-class in that function, the relationships of production even to capital and labor inputs, much less to the variety of technological and social and human capital elements that enter a specification of endogenous productivity change (Solow 1957; Romer 1994), involve multiple agent-classes. In the representation of the market now in IFs there are also many key agent-class relationships as suggested by the table.
Financial Flows/Social Accounting
| System/Subsystem | Financial |
| Organizing Structure | Market plus socio-political transfers in Social Accounting Matrix (SAM) |
| Stocks | Government, firm, household assets/debts |
| Flows | Savings, consumption, FDI, foreign Aid, IFI credits/grants, government expenditures (military, health, education, other) and transfers (pensions and social transfers) |
| Key Aggregate Relationships
(illustrative, not comprehensive) |
Exchange rate, movements with net asset/current account level; interest rate movements with savings and investment |
| Key Agent-Class Behavior Relationships
(illustrative, not comprehensive) |
Household savings/consumption;
|
Households, firms, and the government interact in markets, but more broadly also via financial flows, including those related to the market (like foreign direct investment), but extending also to those that have a socio-political basis (like government to household transfers). A key structural representation is the Social Accounting Matrix (SAM).
The structural system portrayed by SAMs is well represented by stocks, flows, and key relationships. Although the traditional SAM matrix itself is a flow matrix, IFs has introduced a parallel stock matrix that captures the accumulation of assets and liabilities across various agent-classes. The dynamic elements that determine the flows within the SAM involve key relationships, such as that which constrains government spending or forces increased revenue raising when government indebtedness rises. Many of these, as indicated in the table, represent agent-class behavior.
The model can represent the behavior of households with respect to use of time for employment and leisure, the use of income for consumption and savings, and the specifics of consumption decisions across possible goods and services. And it represents the behavior of governments with respect to search for income and targeting of transfers and expenditures, in interaction with other agents including households, firms, and international financial institutions (IFIs).
IFs thus represents equilibrating markets (domestically and globally) in goods and services and in financial flows. It does not yet include labor market equilibration.
- ↑ That is normally true, if the labor informal share exceeds the GDP informal share, implying that labor in the informal economy is less productive than that in the formal economy.