Agriculture: Difference between revisions
No edit summary |
No edit summary |
||
| Line 164: | Line 164: | ||
First, a scaling factor cD is calculated in the first year of the model. This is basically the constant in the Cobb-Douglas formulation for estimating yields. It is based upon the base year yield (YL), capital (KAG), and labor supply (LABS). The labor supply is adjusted using a Cobb-Douglass alpha exponent (CDALF) which is explained in detail below. cD is similar to the shift factors elsewhere in the model, which are used to match predicted values in the base year to actual values. It does not change over time. It is computed using the following equation, | First, a scaling factor cD is calculated in the first year of the model. This is basically the constant in the Cobb-Douglas formulation for estimating yields. It is based upon the base year yield (YL), capital (KAG), and labor supply (LABS). The labor supply is adjusted using a Cobb-Douglass alpha exponent (CDALF) which is explained in detail below. cD is similar to the shift factors elsewhere in the model, which are used to match predicted values in the base year to actual values. It does not change over time. It is computed using the following equation, | ||
<!--[if gte msEquation 12]><m:oMathPara><m:oMath><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>cD</m:r></span></i></m:e><m:sub><i style='mso-bidi-font-style: | |||
normal'><span style='font-family:"Cambria Math",serif;color:#252525'><m:r>r</m:r></span></i></m:sub></m:sSub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>=</m:r></span></i><m:f><m:fPr><span style='font-family: | |||
"Cambria Math",serif;mso-ascii-font-family:"Cambria Math";mso-hansi-font-family: | |||
"Cambria Math";color:#252525;font-style:italic;mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:fPr><m:num><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>YL</m:r></span></i></m:e><m:sub><i style='mso-bidi-font-style: | |||
normal'><span style='font-family:"Cambria Math",serif;color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>t</m:r><m:r>=1</m:r></span></i></m:sub></m:sSub></m:num><m:den><m:sSubSup><m:sSubSupPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubSupPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>KAG</m:r></span></i></m:e><m:sub><i style='mso-bidi-font-style: | |||
normal'><span style='font-family:"Cambria Math",serif;color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>t</m:r><m:r>=1</m:r></span></i></m:sub><m:sup><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>CDALF</m:r></span></i></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>s</m:r><m:r>=1</m:r></span></i></m:sub></m:sSub></m:sup></m:sSubSup><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>*</m:r></span></i><m:sSubSup><m:sSubSupPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubSupPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>LABS</m:r></span></i></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>S</m:r><m:r>=1,</m:r><m:r>t</m:r><m:r>=1</m:r></span></i></m:sub><m:sup><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>(1-</m:r></span></i><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>CDALF</m:r></span></i></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>s</m:r><m:r>=1</m:r></span></i></m:sub></m:sSub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>)</m:r></span></i></m:sup></m:sSubSup></m:den></m:f></m:oMath></m:oMathPara><![endif]--> | |||
Second, a target growth rate in yield is computed (TgrYli) which is used in forecast years to restrict the growth rate of the yield. This target growth is a function of current crop demand (AGDEM), expected crop demand (Etdem), and a target growth rate in cropland. | Second, a target growth rate in yield is computed (TgrYli) which is used in forecast years to restrict the growth rate of the yield. This target growth is a function of current crop demand (AGDEM), expected crop demand (Etdem), and a target growth rate in cropland. | ||
[Tgryli | |||
<!--[if gte msEquation 12]><m:oMathPara><m:oMath><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>Tgryli</m:r></span></i></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r></span></i></m:sub></m:sSub><i style='mso-bidi-font-style: | |||
normal'><span style='font-family:"Cambria Math",serif;color:#252525'><m:r>=</m:r></span></i><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><m:f><m:fPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:fPr><m:num><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>Etdem</m:r></span></i></m:num><m:den><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>AGDEM</m:r></span></i></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>s</m:r><m:r>=1</m:r></span></i></m:sub></m:sSub></m:den></m:f><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>-</m:r><m:r>1-</m:r></span></i><b style='mso-bidi-font-weight: | |||
normal'><span style='font-family:"Cambria Math",serif;color:#252525'><m:r><m:rPr><m:scr | |||
m:val="roman"/><m:sty m:val="b"/></m:rPr>tgrld</m:r></span></b></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r></span></i></m:sub></m:sSub></m:oMath></m:oMathPara><![endif]--> | |||
where | where | ||
tgrld is a country-specific parameter indicating target growth in crop land | |||
'''''tgrld''''' is a country-specific parameter indicating target growth in crop land | |||
Etdem is an initial year estimate of the sum of industrial, feed and food demand for crops in the following year | Etdem is an initial year estimate of the sum of industrial, feed and food demand for crops in the following year | ||
Forecast years | |||
===== '''Forecast years''' ===== | |||
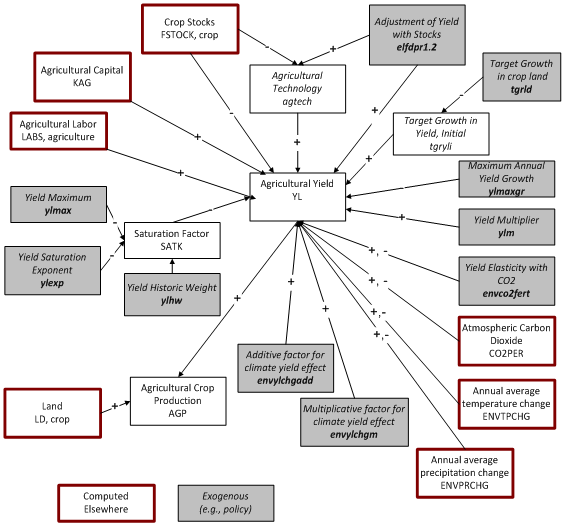
In forecast years, IFs computes yield in stages. The first provides a basic yield (byl) representing change in long-term factors such as capital, labor and technology. The second stage uses this basic yield as an input and modifies it based on prices, so as to represent changes in shorter-term factors (e.g. amounts of fertilizer used, even the percentage of land actually under cultivation). Finally, in a third stage, yields are adjusted in response to changing climate conditions. | In forecast years, IFs computes yield in stages. The first provides a basic yield (byl) representing change in long-term factors such as capital, labor and technology. The second stage uses this basic yield as an input and modifies it based on prices, so as to represent changes in shorter-term factors (e.g. amounts of fertilizer used, even the percentage of land actually under cultivation). Finally, in a third stage, yields are adjusted in response to changing climate conditions. | ||
'''''<u>First stage (Adjustment for long-term factors)</u>''''' | |||
The equations for KAG and LABS are described elsewhere (see sections 3.9 and the economic model, respectively). | |||
The basic yield (Byl) relates yield to agriculture capital (KAG), agricultural labor (LABS), technological advance (Agtec), a scaling parameter (cD), an exponent (CDALF), and a saturation coefficient (Satk). | |||
| |||
[ | |||
[[File:]] | |||
[ | |||
The equations for KAG and LABS are described elsewhere (see sections 3.9 and the economic model, respectively). | |||
*cD is the scaling factor calculated in the first year of the model. Its calculation is described in the section above | |||
*CDALF is the standard Cobb-Douglas alpha reflecting the relative elasticities of yield to capital and labor. It is computed each year in a function, rooted in data on factor shares from the Global Trade and Analysis Project, driven by GDP per capita at PPP.[[#_ftn1|[1]]] | |||
*Agtec is a factor-neutral technological progress coefficient similar to a multifactor productivity coefficient. It is initially set to 1 and changes each year based upon a technological growth rate (YlGroTech). Its computation is described below. | |||
[[File:]] | |||
*The saturation coefficient Satk is a multiplier of the Cobb-Douglas function and of the technological change element. It is the ratio of the gap between a maximum possible yield (YLLim) and a moving average of yields to the gap between a maximum possible yield and the initial yield, raised to an exogenous yield exponent ('''''ylexp'''''). With positive parameters the form produces decreasing marginal returns. | |||
[[File:]] | |||
where | where | ||
ylexp is a global parameter | Syl<sub>r</sub> is a moving average of byl, the historical component of which is weighted by 1 minus the user-controlled global parameter '''''ylhw'''''. | ||
The maximum possible yield (YLLim) is estimated for each country and can change over time. | |||
[ | '''''ylexp'''''is a global parameter | ||
The maximum possible yield (YLLim) is estimated for each country and can change over time. It is calculated as the maximum of 1.5 times the initial yield (YL<sub>r,t=1</sub>) and the multiple of an external user-controlled parameter ('''''ylmax''''') and an adjustment factor (YLMaxM). | |||
[[File:]] | |||
where | where | ||
ylmax is a country-specific parameter | |||
'''''ylmax''''' is a country-specific parameter | |||
The adjustment factor YLMaxM allows for some additional growth in the yields for poorer countries | The adjustment factor YLMaxM allows for some additional growth in the yields for poorer countries | ||
[ | |||
[[File:]] | |||
where | where | ||
DevWeight<sub>r</sub> is GDPPCP<sub>r</sub>/30, with a maximum value of 1 | |||
YlMaxFound is the maximum value of YL found in the first year | YlMaxFound is the maximum value of YL found in the first year | ||
Box1: Computation of technological growth rate for yield | |||
The algorithmic structure for computing the annual values of YlGroTech involves four elements: | {| border="1" cellspacing="0" cellpadding="0" | ||
|- | |||
| style="width:575px;" | | |||
'''<u>Box1: Computation of technological growth rate for yield</u>''' | |||
The algorithmic structure for computing the annual values of YlGroTech involves four elements: | |||
<ol style="list-style-type:lower-alpha;"> | |||
<li>The difference between a targeted yield growth calculated the first year and the portion of that growth not initially related to growth of capital and labor (hence the underlying initial technology element of agricultural production growth); call it AgTechInit.</li> | |||
<li>The gap between desired global crop stock levels and actual stocks (hence the global pressure for technological advance in agriculture); call it AgTechPress. This contribution is introduced by way of the ADJUSTR function of IFs. [[#_ftn2|[2]]]</li> | |||
<li>The difference between the productivity of the agricultural sector calculated in the economic model and the initial year's value of that (hence reflecting changes in the contributions of human, social, physical, and knowledge capital to technological advance of the society generally); call if AgMfpLt.</li> | |||
<li>The degree to which crop production is approaching upper limits of potential; this again involves the saturation coefficient (Satk).</li> | |||
</ol> | |||
The algorithmic structure this is: | The algorithmic structure this is: | ||
Second stage of yield calculation (short term factors) | [[File:]] | ||
Before moving to the next stage, a check is made to see if the growth in byl is within reason. | |||
At this point, the basic yield (byl) is further adjusted by a number of factors. | |} | ||
[ | |||
| |||
'''''<u>Second stage of yield calculation (short term factors)</u>''''' | |||
Before moving to the next stage, a check is made to see if the growth in byl is within reason. Specifically, Byl is not allowed to exceed the moving average of Byl (Syl) times a given growth rate (YlGrbound). This bound is the maximum of a user-controlled global parameter - '''''ylmaxgr''''' and an initial country specific target growth rate (Tgryli<sub>r</sub>).[[#_ftn3|[3]]] | |||
At this point, the basic yield (byl) is further adjusted by a number of factors. The first of these is a simple country-specific user-controlled multiplier – '''''ylm'''''. This can be used to represent the effects of any number of exogenous factors, such as political/social management (e.g., collectivization of agriculture). | |||
[[File:]] | |||
The basic yield represents the long-term tendency in yield but agricultural production levels are quite responsive to short-term factors such as fertilizer use levels and intensity of cultivation. Those short-term factors under farmer control (therefore excluding weather) depend in turn on prices, or more specifically on the profit (FPROFITR) that the farmer expects. Because of computational sequence, we use domestic food stocks as a proxy for profit level. Note that this adjustment is distinct from the adjustment above where global stocks affect the technological growth rate. | The basic yield represents the long-term tendency in yield but agricultural production levels are quite responsive to short-term factors such as fertilizer use levels and intensity of cultivation. Those short-term factors under farmer control (therefore excluding weather) depend in turn on prices, or more specifically on the profit (FPROFITR) that the farmer expects. Because of computational sequence, we use domestic food stocks as a proxy for profit level. Note that this adjustment is distinct from the adjustment above where global stocks affect the technological growth rate. | ||
The stock adjustment factor uses the ADJSTR function to calculate an adjustment factor related to the current stocks, the recent change in stocks, and a desired stock level. | |||
The stock adjustment factor uses the ADJSTR function to calculate an adjustment factor related to the current stocks, the recent change in stocks, and a desired stock level. The desired stock level is given as a fraction (Agdstl) of the sum of crop demand (AGDEM<sub>f=1</sub>) and crop production (AGP<sub>f=1</sub>). Agdstl is set to be 1.5 times '''''dstl''''', which is a global parameter that can be adjusted by the user. | |||
The focus in IFs on yield response to prices differs somewhat from the normal use of price elasticities of supply. For reference, Rosegrant, Agcaoili-Sombila, and Perez (1995: 5) report that price elasticities for crops are quite small, in the range of .05 to .4. | The focus in IFs on yield response to prices differs somewhat from the normal use of price elasticities of supply. For reference, Rosegrant, Agcaoili-Sombila, and Perez (1995: 5) report that price elasticities for crops are quite small, in the range of .05 to .4. | ||
Third stage of yield calculation (Adjustment for a changing climate) | |||
In the third stage, IFs considers the potential effects of a changing climate on crop yields. This is introduced through the variable ENVYLCHG | '''''<u>Third stage of yield calculation (Adjustment for a changing climate)</u>''''' | ||
[ | |||
In the third stage, IFs considers the potential effects of a changing climate on crop yields. This is introduced through the variable ENVYLCHG[[#_ftn4|[4]]] which is calculated in the environmental model. This variable consists of two parts: the direct effect of atmospheric carbon dioxide concentrations and the effects of changes in temperature and precipitation. | |||
[[File:]] | |||
| |||
The direct effect of atmospheric carbon dioxide assumes a linear relationship between changes in the atmospheric concentration from a base year of 1990 and the percentage change in crop yields. | The direct effect of atmospheric carbon dioxide assumes a linear relationship between changes in the atmospheric concentration from a base year of 1990 and the percentage change in crop yields. | ||
[ | |||
[[File:]] | |||
where | where | ||
envco2fert is a global, user-controllable parameter | |||
'''''envco2fert''''' is a global, user-controllable parameter | |||
The effect of changes in annual average temperature and precipitation are based upon two assumptions: 1) there is an optimal temperature (Topt) for crop growth, with yields falling both below and above this temperature and 2) there is a logarithmic relationship between precipitation and crop yields. | |||
CO2PPM<sub>t=1990</sub> is hard coded as 354.19 parts per million | |||
The effect of changes in annual average temperature and precipitation are based upon two assumptions: 1) there is an optimal temperature (Topt) for crop growth, with yields falling both below and above this temperature and 2) there is a logarithmic relationship between precipitation and crop yields. The choice of this functional form was informed by work reviewed in Cline (2007). Together, these result in the following equation: | |||
[[File:]] | |||
[[File:]] | |||
where | where | ||
T0 and P0 are country-specific annual average temperature (degrees C) and precipitation (mm/year) for the period 1980-99. | T0 and P0 are country-specific annual average temperature (degrees C) and precipitation (mm/year) for the period 1980-99. | ||
DeltaT and DeltaP are country specific changes in annual average temperature (degrees C) and precipitation (percent) compared to the period 1980-99. | |||
Topt is the average annual temperature at which yield is maximized. | DeltaT and DeltaP are country specific changes in annual average temperature (degrees C) and precipitation (percent) compared to the period 1980-99. These are tied to global average temperature changes and described in the documentation of the IFs environment model. | ||
Topt is the average annual temperature at which yield is maximized. It is hard coded with a value of 0.602 degrees C. | |||
SigmaTsqd is a shape parameter determining how quickly yields decline when the temperature moves away from the optimum. It is hard coded with a value of 309.809. | SigmaTsqd is a shape parameter determining how quickly yields decline when the temperature moves away from the optimum. It is hard coded with a value of 309.809. | ||
CO2Fert and ClimateEffect are multiplied by each other to determine the effect on crop yields. | CO2Fert and ClimateEffect are multiplied by each other to determine the effect on crop yields. | ||
There are two final checks on crop yields. | |||
[AGP] | There are two final checks on crop yields. They are not allowed to be less than one-fifth of the estimate of basic yield (Byl) and they cannot exceed the country-specific maximum ('''''ylmax''''') or 100 tons per hectare. Finally crop production is adjusted for production losses to arrive at post loss production (AGP). Losses are discussed in detail in section 3.1.4 below | ||
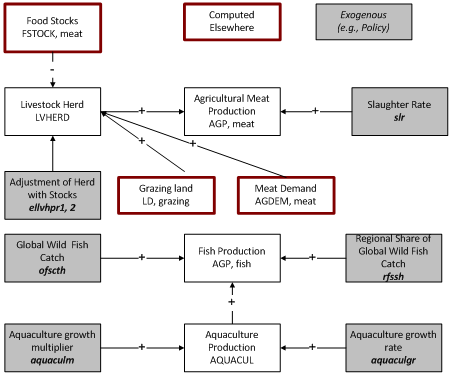
==== Meat Production ==== | |||
Meat production in IFs is the sum of animal meat production and non-meat animal products (AGPMILKEGGS). Animal meat production in a particular country is a function of the herd size and the slaughter rate and non-animal meat products are calculated by applying a ratio MilkEggstoMeatI which is calculated in the first year of the model as the ratio of non-meat animal production to the meat production. Meat production is then adjusted for production losses which are described in detail in section 3.1.4 below. | |||
| |||
[[File:]] | |||
Where, | |||
LVHERD is the size of livestock in a particular country in a particular year | |||
'''''slr'''''is the slaughter rate which is a global parameter | |||
AGLOSSPROD is the meat production loss. | |||
==== '''Pre-processor and first year''' ==== | |||
In the pre-processor, meat production is initialized in the model using data from the FAO food balance sheets. Total meat production and animal meat production (which is the sum of bovine meat production, mutton and goat meat production, pig meat production, poultry meat prod, and other meat production) are initialized separately. If data on all of the animal meat sub-categories is unavailable, then Animal meat production is calculated as 30 percent of total meat production. Animal production is also not allowed to exceed 99% of the value of total meat production. | |||
| |||
AGPMILKEGGS, which is the non-meat animal production is then calculated as total meat production minus total animal meat production. The non-meat production ratio MilkEggstoMeatI is calculated as the ratio of the initialized value of AGPMILKANDEGGS and meat production in the first year. This is used in forecast years to calculate the value of non-meat animal production, and is held constant over time. | |||
| |||
[[File:]] | |||
| |||
The size of the livestock (LVHERD) is also computed in the first year using the initialized value of pre-loss meat production. This value of LVHERD is used in forecast years to compute meat production. | |||
| |||
[[File:]] | |||
| |||
For a detailed discussion on the dynamics of livestock herd, refer to section 3.11 of this document. | |||
===== '''Forecast years''' ===== | |||
Pre-production loss values for meat production are calculated in IFs as meat production (AGPppl) and production of non-meat animal products (AGPMILKANDEGGS). Meat production, in metric tons, is given as the multiple of the herd size (LVHERD) and the slaughter rate ('''''slr'''''). The latter is a global parameter. These values are then adjusted for production losses for meat (AGPRODLOSS) to arrive at post production loss values (AGP). The same meat production loss percentage is also applied to the non-meat production to arrive at post loss production values for the variable. The dynamics of production losses are discussed in section 3.1.4 | |||
[[File:]] | |||
Where, | |||
[[File:]] | |||
Production of non-animal meat products is computed using the non-meat production ratio which is applied to the animal meat production. | |||
[[File:]] | |||
The dynamics of the livestock herd are described in section 3.11. | |||
<div> | |||
==== Fish Production ==== | |||
The production of fish has two components, wild catch and aquaculture. Fish caught through aquaculture is treated as a stock in the model and is a function of a growth component. Wild catch on the other hand is treated as a flow in the model. | |||
===== '''<u>Pre-processor and first year</u>''' ===== | |||
'''<u></u>''' | |||
Data for fish catch and aquaculture is derived through two main sources, namely the FAO food balance sheets and the FAO Fishstatj software. Data for fish production, imports and exports is initially extracted from the FAO Food Balance Sheets. However, no breakout is available for fish caught as wild catch and fish caught through aquaculture. This bifurcation is available in the dataset from the FAO Fishstatj database. The data from the FAO food balance sheets is broken down into fish catch (AGFISHCATCH) and aquaculture (AQUACUL) using data from the FAO fishstatj dataset. | |||
| |||
In the first year, the values for pre-loss production of wild fish, AGFISHCATCHppl and aquaculture, AQUACULppl, are calculated by adding in a level of catch loss, which is not reflected in the FAO and Fishstatj data. Separate parameters, '''''aglossprodperc'''''<i><sub>f=3</sub> </i>''and '''aglossprodperc'''<sub>f=4</sub>, ''are used for wild catch and aquaculture. | |||
===== '''Forecast years''' ===== | |||
The amount of aquaculture (AQUACUL) in forecast years can be modified by the user. Production is assumed to grow over time. The default growth rate in the first year for all countries is 3.5 percent, but this value can be modified by the user, by country, with the parameter '''''aquaculgr'''''. This growth rate declines to 0 over a number of years given by the global parameter '''''aquaculconv'''''. Users can change the amount of aquaculture production, by country, with the multiplier '''''aquaculm[[#_ftn1|'''[1]''']]'''''. Finally, this is adjusted for production losses from aquaculture with Aquaculloss | |||
[[File:]] | |||
where | |||
''aquaculgr<sub>r,t</sub> declines from '''aquaculgr'''<sub>r,t=1</sub>'' to 0 over '''''aquaculconv''''' years | |||
Wild catch is initialized in the pre-processor as the variable AGFISHCATCH. The pre- production loss of wild catch is computed after applying a multiplier '''''fishcatchm''''' and this is adjusted for losses[[#_ftn2|[2]]] (Catchloss) to arrive at post production loss wild fish catch. | |||
[[File:]] | |||
Total, post-production loss fish production (AGP) is then given as: | |||
[[File:]] | |||
<div><br/><div id="ftn2"> | |||
</div></div> | |||
==== '''<u></u>''''''Losses and waste''' ==== | |||
Losses can occur at several places along the chain from production. In earlier sections, we mentioned losses at the production stage. Losses can also occur in the process of transmission and distribution from the producer to the final consumer and at the consumer stage. The latter is sometimes referred to as food waste, but for our purposes, we will use the term loss for all three stages: production, transmission and distribution, and consumption. | |||
The FAO Food Balance Sheets provide data on losses during transmission and distribution, but not at the production or consumption stages. Until we are able to find data showing a clear relationship between these losses and GDP per capita, or some other explanatory factor, we make an assumption of production losses and consumption losses of 10% for all countries. The user can make changes in these values with the parameters '''''aglossprodperc'''''<i>and'''''aglossconsperc'''''respectively. The former can be set for crops, meat, wild catch, and aquaculture separately. The latter combines wild catch and aquaculture as fish, as we do not have separate data on the consumption of wild caught versus farmed fish. More details on the use of these parameters and the actual calculation of production and consumption losses are provided in sections 3.1.1-3.1.3 and 3.2.1, respectively. | |||
Turning to transmission and distribution losses, some agricultural commodities will never make it from the producer to the final consumer because of pests, spoilage, etc. The FAO food balance sheets provide data on food lost to waste for crops and meat , but not for fish. Thus, for now we assume that there are no losses in this stage for fish. For crops and meat, though we were able to establish relationships between transmission and distribution losses and GDP per capita. These are shown in the figures below: | |||
---- | |||
===== '''Pre-processor and first year''' ===== | |||
The initial values for transmission and distribution losses are taken directly from the FAO Food balance sheets. For those countries without data, an assumed loss of 1 ton (0.000001 MMT) is used. These are given by the variable AGLOSSTRANS[[|<sub>r, f=1-3</sub>]]. As with consumption, wild catch and aquaculture are combined into a single category, fish, as we do not have separate data; also, for the moment the value of AGLOSSTRANS<sub>r, f=3</sub> is set to 0 for all countries. | |||
In the first year, a ratio of [[transmission/distribution loss to food demand]], FDEM, is computed as: | |||
<!--[if gte msEquation 12]><m:oMathPara><m:oMath><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>AgLossTransToFoodRatI</m:r></span></i></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>f</m:r><m:r>=1</m:r><m:r>to</m:r><m:r>3</m:r></span></i></m:sub></m:sSub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>=</m:r></span></i><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>AGLOSSTRANS</m:r></span></i></m:e><m:sub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>f</m:r><m:r>=1</m:r><m:r>to</m:r><m:r>3</m:r></span></i></m:sub></m:sSub><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>/</m:r></span></i><m:sSub><m:sSubPr><span | |||
style='font-family:"Cambria Math",serif;mso-ascii-font-family:"Cambria Math"; | |||
mso-hansi-font-family:"Cambria Math";color:#252525;font-style:italic; | |||
mso-bidi-font-style:normal'><m:ctrlPr></m:ctrlPr></span></m:sSubPr><m:e><i | |||
style='mso-bidi-font-style:normal'><span style='font-family:"Cambria Math",serif; | |||
color:#252525'><m:r>FDEM</m:r></span></i></m:e><m:sub><i style='mso-bidi-font-style: | |||
normal'><span style='font-family:"Cambria Math",serif;color:#252525'><m:r>r</m:r><m:r>,</m:r><m:r>f</m:r><m:r>=1</m:r><m:r>to</m:r><m:r>3</m:r></span></i></m:sub></m:sSub></m:oMath></m:oMathPara><![endif]--> | |||
<div id="ftn1"> | |||
===== '''Forecast years''' ===== | |||
In future years, for crops and meat, the initial estimate for transmission and distribution losses are calculated as follows: | |||
· Predictions are made for the ratio of transmission/distribution loss to food demand as a function of GDP per capita (predaglosstrans) for the first year and the current year. | |||
· The ratio of the predicted values for the current year to the predicted value for the first year is multiplied by AgLossTransToFoodRatI. | |||
· That result is multiplied by FDEM for the current year to get losses in MMT. | |||
· That result is multipled by the parameter '''''aglosstransm''''', to get a final value. | |||
| |||
This can be expressed as: | |||
Some further adjustments may be made to AGLOSSTRANS in the process of balancing global trade and balancing domestic supply and demand. These are discussed later in this documentation. | |||
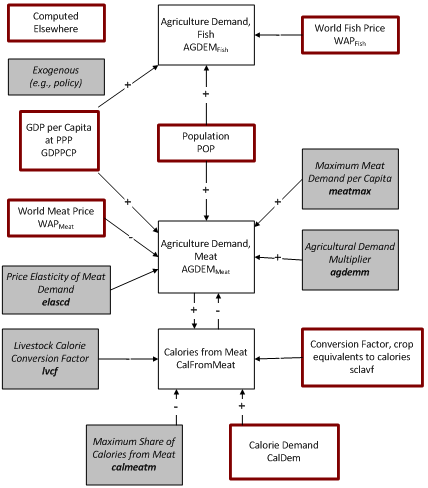
== Agricultural Demand == | |||
IFs computes demand, or uses, for three agricultural categories—crops, meat, and fish. These commodities are used for direct human consumption (FDEM), animal feed (FEDEM), industrial uses, e.g. biofuels (INDEM), and food processing and manufacturing (FMDEM). IFs also tracks the losses in transmission and distribution (AGLOSSTRANS). Total demand (AGDEM) is the sum of these five use categories and is given in MMT per year. | |||
Section 3.1.4 describes the calculation of AGLOSSTRANS, so that is not repeated here. The calculation of the demand for direct human consumption, FDEM begins with estimates of daily per capita calorie demand for crops, meat, and fish. Briefly, IFs first estimates total per capita calorie demand, which responds to GDP per capita (as a proxy for income). The division of total demand between demand for calories from crops and from meat and fish also changes in response to GDP per capita (more meat and fish demand with increasing income). Finally, the division of calories from meat and fish is calculated based on historic patterns. Using country and commodity specific factors, the daily per capita calorie demands are converted to grams per capita per day and protein per capita per day. The grams per capita per day are then multiplied by the size of the population, POP, and the number of days in a year, 365, to arrive at FDEM. | |||
The other demands, FEDEM, INDEM, and FMDEM are driven by factors such as the size of the livestock herd, LVHERD, and the use of crops for fuel production. In cases where information is lacking, these demands are determined in relation to FDEM. Finally, there may be some modifications to all of the demand categories due to shortages or other factors, as described in the rest of this section. | |||
=== [['''3.2.1 Daily per capita demands – calories, grams, and protein''']] === | |||
IFs tracks one set of variables for agricultural demands, or uses, on a daily per capita basis. These are. specifically, calories (CLPC), protein (PROTEINPC), and grams (GRAMSPC), for each category – crops, meat, and fish. | |||
==== '''Pre-processor and first year''' ==== | |||
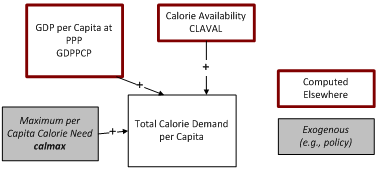
Daily calories per capita (CLPC), by category, are initialized in the IFs pre-processor using data from the FAO food balance sheets. Data on daily protein per capita and grams per capita are also read into the pre-processor.[[#_ftn1|[1]]] If data are available for crops, meat, and fish, total values for calories, protein, and grams are calculated as sums of the three categories. For countries where no data are available for one or more of the categories, the model follows a set of procedures to fill in the missing data. These procedures uses, among other things, 1) equations that relate total calories per capita per day and the share of these calories from crops versus meat and fish to GDP per capita and 2) other ratios derived from global averages of those countries with data. Later in the pre-processor, CLAVAL, which represent the total calories (across all categories) per day for the population as a whole is also calculated. | |||
The equation for total calories as a function of GDP per capita is stored as "GDP/Capita (PPP 2011) Versus Calorie Demand (fixed-effect)" and is illustrated below.[[#_ftn2|<sup><sup>[2]</sup></sup>]] | |||
[[File:]] | |||
Figure 13: Calories per capita vs GDP per capita at PPP | |||
The equation for the share of calories from meat and fish as a function of GDP per capita is stored as " GDP/Capita (PPP 2011) Versus CLPC from MeatandFish (2010) Log" | |||
Both of these are in a logarithmic form, indicating that both total calories and the share of calories from meat and fish increase with GDP per capita, but at a decreasing rate. As the data do not show a clear pattern for the breakdown between meat and fish, which is largely due to cultural patterns and geography, the model uses historical values rather than an estimated equation, as discussed below. In the pre-processor, an average global value is used for countries without data. | |||
In the first year of the model, one of the first things that occurs is a recalculation of GRAMSPC as GRAMSPC = FDEM/(POP * 365) * 100000. This is to ensure the consistency between the daily per capita variable, GRAMSPC, and the annual national value, FDEM. This is necessary because FDEM may have been modified in the pre-processor as part of ensuring a balance between the initial year supply of agricultural produces and their use. This is described in more detail in Box 1. | |||
In addition, a number of additional values related to calories to be used in the forecast period are calculated. | |||
#CalActPredRat: the ratio between actual calories available and the predicted value.[[#_ftn3|[3]]] It is used as a multiplicative shift factor. The predicted level of is estimated using the equation for total calories per capita as a function of GDP per capita described above. This is bound from above by an assumed maximum value, given by the global parameter '''''calmax'''''. The value of calactpredrat gradually converges to 1 over a period given by the global parameter '''''agconv''''' and appears in future equations with the name AdjustForInitialDevc. | |||
#MeatAndFishActPredRat: the ratio between actual share of calories from meat and fish to the predicted value. It is used as a multiplicative shift factor. The predicted level of is estimated using the equation for share of calories from meat and fish per capita as a function of GDP per capita described above. | |||
#MeatToMeatFishRatI: the ratio between calories from meat and calories from meat and fish. It is used to separate the future estimates of calories from meat and fish into separate values for meat and fish. | |||
#ProtToCalRatI: the ratio of daily per capita protein to daily per capita calories, by category. It is used to convert future estimates of calorie availability to protein availability. If for some reason the initial estimate of ProtToCalRatI is 0 for any category, the median value for that category based on 2010 is used. | |||
#GramsToCalRatI: the ratio of daily per capita grams to daily per capita calories, by category. It is used to convert future estimates of calorie availability to a value in grams, which is then used to estimate aggregate demand for food for direct human consumption. If for some reason the initial estimate of GramsToCalRatI is 0 for any category, the median value for that category based on 2010 is used. | |||
==== '''Forecast years''' ==== | |||
In the forecast years, daily per capita calorie demand begins with a prediction of a total demand, CalPerCap, as a function of average income using the equation above, with a maximum value given by '''''calmax'''''. Two other values are also calculated at this point. First, a base level of calories per capita, CalBase, is also calculated, which is given as the minimum of 3000 or '''''calmax''''' minus 300. Second, because comparative cross sections show a growth of around 7.6 calories per capita per year independent of average income, a factor representing this increase (CaldGr) is calculated as: | |||
[[File:]] | |||
Thus, depending on the exact values of '''''calmax''''', CalBase, and CalPerCap, CaldGr grows each year by a value that centers around 7.6 calories. This value is then added to the predicted value in calculating the total demand for calories. | |||
The equation also takes into account '''''calmax''''' and the multiplicative shift factor on calories per capita calculated in the first year of the model. The latter is named AdjustForinitialDevc, which, as noted previously, is calculate as the value of calactpredrat gradually converging to 1 over a period given by the global parameter '''''agconv''''' | |||
[[File:]] | |||
Finally, a value for the total calories per day, CalDem, is calculated by multiplying TotalCalPerCap times POP. | |||
The next step is to divide the total calories between crops and meat plus fish. First, a predicted value of the share of total calories going to meat and fish, MeatAndFishPctPred, is calculated as a function of GDP per capita, using the equation described earlier. Second, the ratio of between actual share of calories from meat and fish to the predicted value, MeatAndFishActPredRat, calculated in the first year is potentially modified. Specifically, a new variable, AdjustForInitialDevm, is assigned either the intial value of MeatAndFishActPredRat, or a value that reflects convergence of MeatAndFishActPredRat to a value of 1 over a period given by the global parameter '''''agconv'''''. The countries for which convergence does not occur are the South Asian countries – India, Nepal and Mauritius – which are traditionally low meat consuming countries. The actual share of calories from meat and fish is then calculated as: | |||
[[File:]] | |||
A minimum value of 3.5 percent is also imposed. | |||
With this value for MeatAndFishPctAct, the model can divide the total calories between crops and the combination of meat and fish. Using the value for MeatToMeatFishRatioI, calculated in the first year, the model can then estimate the calories from meat and fish separately. The values are stored in the variable CLPC(<sub>r,f)</sub> | |||
At this point, these values are adjusted for changes in world food prices and elasticities to demand for these prices. | |||
[[File:]] | |||
''where'' | |||
WAP<sub>f=1-3</sub> are the global food prices for crops, meat, and fish | |||
X is the price elasticity of demand and takes on the value of '''''elascd''''', '''''elasm''''', and '''''elasfd'''''for crops, meat, and fish, respectively | |||
Given these adjustments, TotalCalPerCap is recalculated as the sum of CLPC for crops, meat, and fish. | |||
Finally, a parameter '''''clpcm''''' is applied to the final value of calories per capita that allows the user to manipulate demand for calories in addition to two parameters (that allow the user to eliminate hunger in a particular country over time) which are described below. | |||
The parameters '''''malnelimstartyr''''' and '''''malnelimtargetyr''''' allow the user to reduce hunger in any country over a specific period of time. The activation of these parameters by the user, calculates the required cumulative growth rate in calories to eliminate hunger (reduce the undernourished population to 5 percent of the total population) ClPCcum. This cumulative growth rate is calculated using a logarithmic function that computes the growth rate relative to the household income and unskilled labor in a country.[[#_ftn4|[4]]] Also, the user can activate a switch '''''malelimprecisesw''''', which calculates the specific number of calories required to eliminate hunger for the most undernourished part of the population. An individual who consumes less than 1000 calories per day but is still alive is assumed to be the most undernourished person in the population. | |||
Therefore the final equation is as follows, | |||
[[File:]] | |||
Where, | |||
clpcm is a multiplier that can be used to affect the demand for calories | |||
ClPCcum is the cumulative growth rate required in calories per capita to eliminate hunger over a specific time period determined by malnelimstartyr and malnelimtargetyr | |||
Caldef is the cumulative number of calories required to eliminate hunger for the most undernourished part of the population. This is calculated through the activation of malelimprecisesw. | |||
At this point, i.e., after dealing with the hunger targets, the values for daily grams per capita (GRAMSPC) and daily protein per capita (PROTEINPC) are calculated by multiplying the values for CLPC by GramsToCalRatI and ProtToCalRatI, respectively. Recall that these values were computed in the first year. | |||
A final adjustment to CLPC, PROTEINPC, and GRAMSPC can occur as a result of shortages. This begins with a reduction in FDEM, as described in Section 3.4: Stocks, which is then translated into new values for GRAMSPC, which are then used to recalculate CLPC and PROTEINPC. | |||
One final variable, CLAVAL, which represent the total calories (across all categories) per day for the population as a whole is then calculated as total calories per capita times the population. | |||
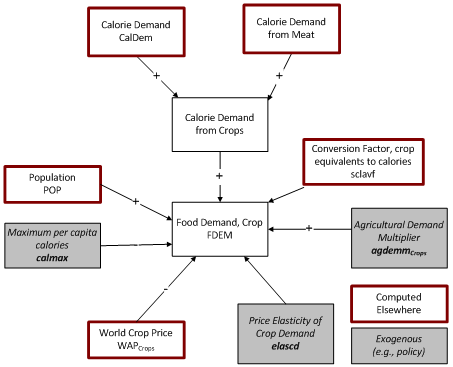
=== [['''3.2.2 Agricultural demand for direct human consumption (FDEM)''']] === | |||
FDEM represents the amount of agricultural commodities going directly to consumers, presumably for consumption. | |||
==== '''Pre-processor and first year''' ==== | |||
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used for direct human consumption, FDEM. If these data are missing for any commodity, a value is calculated by multiplying the daily grams per capita by the size of the population (POP) and the numbers of days in a year (365), and then divided by 100000 to get the units correct. As noted in Box 1, certain adjustments may be made to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries. | |||
No adjustments are made to FDEM in the first year. | |||
==== '''Forecast years''' ==== | |||
In the forecast years, FDEM is initially calculated based upon the calculation of daily grams per capita described in section 3.2.1: | |||
[[File:]] | |||
There are two situations where the value of FDEM might be adjusted. The first case is where more than 85 percent of consumers’ expenditures are on food stuffs. If this is the case, the values of FDEM for crops and meat and fish are reduced proportionately, as described in section 3.2.5. | |||
The second case is when a country faces absolute shortages, i.e., the total domestic supply, AGDEM, is not adequate to meet all of the demands, FDEM + FEDEM + INDEM + AGLOSSTRANS even after drawing down stocks to 0. Here, each of these demands/uses are reduced proportionately to restore the balance as described in Section 3.4: Stocks. In both cases, the decreases in FDEM are fed forward to reduce the actual calories available, as described in section 3.2.1. | |||
=== [[3.2.3 Feed demand for crops, meat and fish]] === | |||
Feed demand, FEDDEM, represents: 1) the amount of crops that are used to complement what livestock receive from grazing, and 2) an unspecified use of meat and fish, which appears in the FAO Food Balance Sheets. | |||
==== '''Pre-processor and first year''' ==== | |||
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used as feed for other agricultural production, usually meat. If data are missing, a minimum value of 1 ton, or .000001 MMT is used. | |||
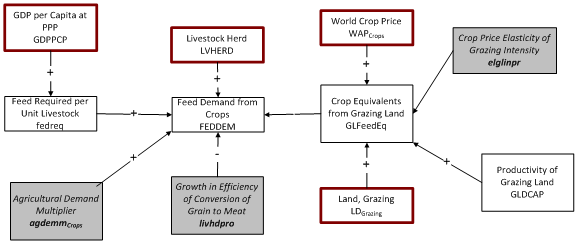
An initial adjustment to feed demand for crops can occur in the pre-processor. This occurs when the production from grazing land is not being fully utilized. Specifically, this is when the amount of equivalent feed from grazing land, i.e. grazing land productivity, here named GLandCAP, implies a lower than assumed minimum value of 0.01 tons of crop equivalents per hectare, here named MinLDProd. The implied value of GLandCap is calculated as the difference between the total feed requirement for the number of livestock minus the feed demand divided by the amount of grazing land. | |||
[[File:]] | |||
''where'' | |||
LiveHerd is the size of the livestock herd (discussed in section ?) | |||
LDGraz is the amount of grazing land (discussed in section 3.10: Land Dynamics) | |||
FEDDEM<sub>r,f=1</sub> is the value for demand for crops for feed | |||
[[File:]]<br/>Fedreq is an estimate of the per animal feed requirements, which is a function of GDP per capita. The function is depicted in the figure below[[#_ftn5|[5]]]: | |||
{| cellpadding="0" cellspacing="0" width="100%" | |||
|- | |||
| <div> | |||
Figure 15: Per animal crop feed demand as a function of GDP per capita | |||
</div> | |||
|} | |||
<br/>If the value of GLandCAP is less than the minimum, MinLDProd—currently hard coded as 0.01 tons of crop equivalents per hectare, based on values for the Saudi desert), then CFEDDEM<sub>r,f=1</sub> is recalculated as the difference between the total feed requirement for the number of livestock minus the amount of feed equivalent produced by grazing using the minimum productivity. | |||
[[File:]] | |||
Note that this occurs when the feed from crops meets most, if not all, of the total feed requirements, implying little or no need for feed equivalents from grazing land. Also a minimum value of 0.01 MMT is set for CFEDDEM. | |||
Finally, as noted in Box 1, certain adjustments may be made in the pre-processor to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries. | |||
In the first year, the model once again checks to make sure that the grazing land productivity exceeds a minimum value and this time stores this value for future use. A parallel equation to that in the pre-processor is used to get an initial estimate for grazing land productivity, now named GldCap: | |||
[[File:]] | |||
''where'' | |||
LVHERD<sub>r,t=1</sub> replaces LiveHerd from the equation in the pre-processor | |||
LD<sub>r,l=2,t=1</sub> replaces LDGraz from the equation in the pre-processor | |||
FEDDEM<sub>r,f=1</sub> replaces CFEDDEM<sub>r,f=1</sub> from the equation in the pre-processor | |||
Fedreq<sub>r</sub> is the same as in the equation in the pre-processor | |||
Now, if the model estimates that GldCAP is below the minimum level, still called MinLDProd and hard coded to a value of 0.01, a new value of GldCAP calculated: | |||
[[File:]] | |||
''where'' | |||
LVHERD<sub>r,t=1</sub>, LD<sub>r,l=2,t=1</sub>, FEDDEM<sub>r,f=1</sub>, and fedreq<sub>r</sub> are defined as above | |||
'''''fedreqm'''''<sub>r</sub> is a multiplier required to ensure that the grazing land productivity meets the difference between the total feed requirement and that provided by crops in the initial year. It is calculated as: | |||
[[File:]] | |||
Note that this value is always greater than or equal to 1 given the condition for making the adjustment. When no adjustment is made, fedreqm is set to 1. These values of GldCAP and fedreqm, calculated in the first year, are held constant for all forecast years | |||
Finally, one other value is calculated in the first year – FeedToFoodRatI, which is the ratio between FEDDEM and FDEM. This is calculated for crops, meat, and fish, but is only used for the latter two categories in the forecast years, as described below. | |||
==== '''Forecast years''' ==== | |||
In the forecast years, FEDDEM is calculated as a function of the size of the livestock herd (LVHERD), the feed requirements per unit livestock (fedreq), the amount of grazing land (LD<sub>l=2</sub>), and the productivity of grazing land (GldCAP), but adjustments are also made reflecting the effect of global crop prices on grazing intensity (WAP<sub>f=1</sub>), changes in the efficiency with which feed is converted into. meat, and the adjustment factor fedreqm calculated in the first year. There is also a parameter with which the user can cause a brute force increase or decrease in FEDDEM ('''''feddemm''''') | |||
The model first calculates the amount of crop equivalent produced from grazing land using the following equation: | |||
[[File:]] | |||
''where'' | |||
LD<sub>r,l=2</sub> is the amount of grazing land; the dynamics of this variable is discussed in section 3.10: Land Dynamics | |||
GldCAP<sub>r</sub> is the country value for grazing land capacity initialized in the first year | |||
WAP<sub>t,f=1</sub> is global price for crops; and | |||
'''''elglinpr''''' is a global parameter for the elasticity of livestock grazing intensity to annual changes in world crop prices; the basic assumption is that increasing prices should lead to increased grazing intensity and therefore greater productivity of grazing land[[#_ftn6|[6]]] | |||
This production of crop equivalents from grazing land is then subtracted from total feed requirement in the following equation: | |||
[[File:]] | |||
''Where'' | |||
LVHERD, fedreq, and fedreqm are as previously described. LVHERD and fedreq are updated each year as described in section 3.11: Livestock Dynamics and as a function of GDP per capita, respectively. fedreqm, determined in the first year, does not change over time. | |||
'''''livhdpro''''' is a global parameter related to the rate at which the productivity of crops in producing meat improves over time. This part of the equation implies that the amount of feed needed to produce a unit of meat declines over time to a minimum of half the original amount required | |||
'''''feddemm''''' is a country-specific multiplier that can be used to increase or decrease crop demand for feed purposes | |||
For meat and fish, a simpler process is used. The feed to food ratio, FeedToFoodRatI, calculated in the initial years of the model is used to calculate the share of feed demand for meat and fish respectively. | |||
[[File:]] | |||
Note that there is no multiplier equivalent to '''''feddemm''''' for meat and fish. | |||
Finally, as with FDEM, FEDDEM may be adjusted to account for excessive consumer spending on food, as described in Box 2 or due to shortages in crops, meat, or fish as described in Section 3.4: Stocks. | |||
=== [['''3.2.3 Industrial demand for crops, meat and fish''']] === | |||
Industrial demand, INDEM, represents the amount of crops, meat, and fish that are used in industrial processes. | |||
==== '''Pre-processor and first year''' ==== | |||
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used in industrial processes. If data are missing, a minimum value of 1 ton, or .000001 MMT is used. | |||
Finally, as noted in Box 1, certain adjustments may be made in the pre-processor to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries. | |||
{| cellpadding="0" cellspacing="0" width="100%" | |||
|- | |||
| <div> | |||
Figure 18: Per capita industrial demand for crops as a function of GDP per capita | |||
</div> | |||
|} | |||
<br/>In the first year, two values related to industrial demand for crops are calculated. The first of these is a multiplicative shift factor (INDEMK), which is calculated as the ratio of actual to predicted industrial demand for crops. The predicted value is given by a function that relates per capita industrial demand to GDP per capita, which is shown [[File:]]<br/>below.[[#_ftn7|[7]]] This multiplicative shift factor remains constant over time. | |||
As with FEDDEM, one other value is calculated in the first year – IndToFoodRatI, which is the ratio between INDEM and FDEM. This is calculated for crops, meat, and fish, but is only used for the latter two categories in the forecast years, as described below. | |||
==== '''Forecast years''' ==== | |||
In the forecast years, for crops, the initial value of industrial demand is updated using the table function above to get a predicted value for industrial demand per capita, which is then multiplied by population (POP) and the multiplicative shift factor (IndemK). At this point, a region-specific multiplier ('''''indemm''''') can either increase or decrease the initial estimate of INDEM. | |||
A first adjustment to INDEM is related to the world energy price (WEP) and reflects the use of crops for fuel production. Specifically, as the world energy price increases relative to the price in the first year, the industrial demand for crops increases. | |||
[[File:]] | |||
''Where'' | |||
WEP is world energy price | |||
FoodforFuel is the elasticity of industrial use of crops to world energy prices. It starts at a value given by the global parameter '''''elagind''''', and declines to a value of 0 over 50 years. | |||
The second adjustment relates to the world crop price (WAP<sub>f=1</sub>); as this increases relative to the price in the first year, industrial demand for crops declines. | |||
[[File:]] | |||
''Where'' | |||
WAP is world crop price | |||
'''''elascd''''' is a global parameter specifying the elasticity of crop demand to global food prices | |||
A third adjustment is based on an assumed cap on per capita industrial demand for crops (IndemCapperPop—hard coded as 2. Specifically, INDEM is not allowed to exceed IndemCapperPop * POP. | |||
For meat and fish, industrial demand is initially calculated by applying the Industrial demand to food ratio, IndToFoodRatI (calculated in the initial year of the model) to the value of food demand. | |||
[[File:]] | |||
Note that there is no multiplier equivalent to '''''indemm''''' for meat and fish. | |||
Finally, as with FDEM and FEDDEM, INDEM may be adjusted to account for excessive consumer spending on food, as described in section 3.2.5 or due to shortages in crops, meat, or fish as described in Section 3.4: Stocks. | |||
=== [[3.2.4 Food manufacturing demand]] === | |||
The final demand category, FMDEM, relates to the use of crops, meat, and fish in food manufacturing and processing. | |||
==== '''Pre-processor and first year''' ==== | |||
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used in food manufacturing and processing.[[#_ftn8|[8]]] Note that If data are missing, a minimum value of 1 ton, or .000001 MMT is used. | |||
As noted in Box 1, certain adjustments may be made in the pre-processor to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries. | |||
Paralleling the case for INDEM, FEDDEM, and AGLOSSTRANS, one other value is calculated in the first year –FManToFoodRatI, which is the ratio between INDEM and FDEM. This is calculated for crops, meat, and fish, and used for all three in the forecast years, as described below. | |||
[[File:]] | |||
==== '''Forecast years''' ==== | |||
In the forecast years, for all three categories, demand is calculated using the Food manufacturing to food demand ratio, FManToFoodRatI, calculated in the first year of the model and the value of food demand. | |||
[[File:]] | |||
As with FDEM, INDEM, and FEDDEM, FMDEM may be adjusted to account for any shortages in crops, meat, or fish as described in Section 3.4: Stocks. It is not currently affected by excessive consumer spending on food, as described in Box 2 | |||
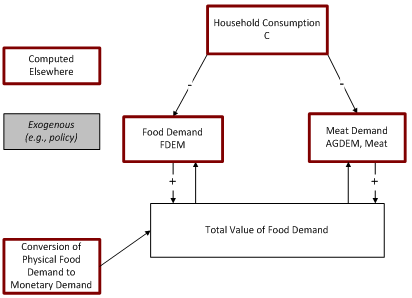
=== [['''3.2.5 Total agricultural demand and final adjustment to demand''']] === | |||
==== '''Pre-processor and first year''' ==== | |||
AGDEM, which represents the sum of all uses. It is initialized in the first year of the model to ensure the balance with production, imports, and exports: | |||
[[File:]] | |||
==== '''Forecast years''' ==== | |||
In the forecast years, AGDEM, is recalculated as the sum of the final values of feed, industry, and food demand and transmission losses: | |||
[[File:]] | |||
Note that this occurs after any adjustments to the demand values as a result of excessive consumer spending on food, (described below), but before adjustments as a result of shortages, describe in Section 3.4: Stocks. Thus, it can be the case that the final value of AGDEM may exceed the sum of the individual demand values. | |||
'''''<u>Final agricultural demand adjustment based on levels of consumer spending</u>''''' | |||
One final adjustment is made to the agricultural demand variables in the forecast years. | |||
If the preliminary estimate of total food demand in monetary terms (csprelim), is too large of a share of consumption, i.e., if | |||
[[File:]] | |||
''Where'' | |||
CSF is the ratio of consumer spending in the agricultural sector in the first year (CS<sub>r,s=1,t=1</sub>) to DemVal<sub>r</sub>, a weighted sum of demands for agricultural products for food in the first year<br/><br/>[[File:]] | |||
C is total household consumption in the first year | |||
When this is the case, a series of steps are taken to bring these values back in line. | |||
#The necessary reduction (NecReduc<sub>r</sub>), which is in monetary terms, is calculated as CsPrelim<sub>r</sub> – 0.85*C<sub>r</sub> | |||
#A reduction factor (ReducFact) for meat and fish, assuming cuts would disproportionately be there, is calculated as<br/>[[File:]] | |||
with a maximum value of 1 or full elimination | |||
#The physical demands for crops for meat and fish in tons (FDEM, categories 2 and 3) are reduced by reducfact, and the values of the meat and fish reduction are saved for the next step | |||
[[File:]] | |||
[[File:]]<br/><br/><br/>[[File:]] ) | |||
#An estimate of the necessary reductions in crops for food, in monetary terms is estimated by subtracting the savings obtained through the reduction in meat demand | |||
<br/>[[File:]] * [[File:]] * [[File:]] | |||
#The physical demand for crops for food (FDEM) is then reduced as follows | |||
<br/>[[File:]] | |||
Note that this ensures that FDEM is not reduced by more than ninety percent. | |||
Finally, given the changes above, the total demand is recalculated as the sum of the final values of feed, industry, and food demand and transmission losses | |||
[[File:]] | |||
{| cellpadding="0" cellspacing="0" width="100%" | |||
|- | |||
| <div> | |||
'''Box 1: Adjustments in the Pre-processor to Ensure Proper Balances''' | |||
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used for direct human consumption, FDEM, feed (FEDEM), industry (INDEM), food manufacturing (FMDEM), as well as transmission losses (AGLOSSTRANS). All of these are measured in MMT per year. At the same time, it reads in data for production (AGP), imports (AGM), exports (AGX), and total domestic supply (AGDOMSUPP)[1]. | |||
A set of conditions should be meet for these variables for each category: | |||
#AGDOMSUPP = AGP + AGM – AGX. This says that total domestic supply equals production plus imports minus exports. This equivalence can be broken if there are changes in stocks, which we will see in forecast years. Currently, however, we assume there are no such changes in the first year. Thus it may be necessary to make adjustment for the equivalence to hold in first year. This is done in the pre-processor, by keeping AGDOMSUPP the same and applying the following three rules:<ol style="list-style-type:lower-alpha;"> | |||
<li>If AGDOMSUPP > AGP + AGM – AGX, i.e., stocks were being drawn down, increase AGP and AGM while reducing AGX.</li> | |||
<li>If AGDOMSUPP < AGP + AGM – AGX, i.e., stocks were being added to, decrease AGP and AGM while increasing AGX.</li> | |||
<li>Make sure that AGP, AGM, and AGX do not fall below a minimum value.</li> | |||
</ol><li>Sum of AGM across countries = Sum of AGX across countries. This says that imports and exports need to match. If they do not, the model calculates the average of the two sums and adjusts AGM and AGX in each country proportionately.</li> | |||
<li>AGP + AGM – AGX = FDEM + FEDEM + INDEM + FMDEM + AGLOSSTRANS. This says that the total domestic supply, which accounts for production losses, has to match the total uses (including losses in transmission and distribution).</li> | |||
</ol> | |||
The pre-processor includes procedures to ensure that these three conditions hold for the initial values in each country. This can lead to minor adjustments in the values for the supply and demand categories. These processes can also lead to changes in related variables, including the production of non-animal meat products (CAGPMILKEGGS), fish catch (AGFISHCATCH), aquaculture production (AQUACUL), the size of the livestock herd (LVHERD), and the breakdown of land areas (LD). The latter occurs because we do not want these processes to change crop yields (YL). | |||
<ol style="list-style-type:lower-alpha;"> | |||
<li> </li> | |||
</ol> | |||
</div> | |||
|} | |||
| |||
| |||
| |||
| |||
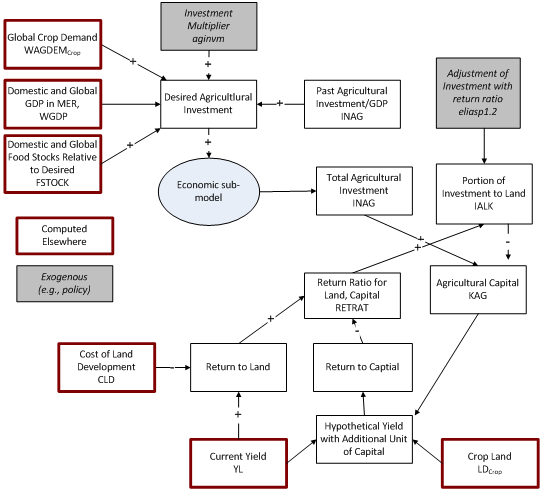
== [[3.3 Trade]] == | |||
Consistent with the approaches within both the economic model and the energy model, trade of agricultural products in IFs uses a pooled approach rather than a bilateral one. That is, we can see the total exports and imports of each country/region, but not the specific volume of trade between any two. Offered exports and demanded imports from each country/region are responsive to the past shares of export and import bases and are summed globally. The average of the totals is taken as the actual level of global trade and the country exports and imports are normalized to that level. | |||
Price differentials across countries do not influence agricultural trade. Although the IFs project has experimented over time with making such trade responsive to prices, there is an increasing tendency globally for food prices to be more closely aligned across countries than was true historically. Moreover, the use within IFs of local relative food surpluses or deficits (as indicated by stock levels) to adjust trade patterns is an effective proxy for the use of prices. | |||
The initial year values of the imports (AGM) and exports (AGX) of the three agricultural commodities in physical quantities are determined in the pre-processor. Since we only have historical data on the imports and exports of fish in monetary terms, these need to be converted to physical terms. This is done by multiplying the monetary values, which are in $billion, by 1000*/2200 to get physical values in million tons. In addition, exports of fish are limited to be less than 70 percent of total fish available and imports less than 1 percent of total fish available. For each of the three agricultural commodity groupings, if there is an imbalance between global imports and global exports in the preprocessor, the latter takes precedence and national imports are adjusted to bring global imports into line with global exports. | |||
In the first year, seven variables are set related to trade for each commodity: XKAVE, MKAVE, XKAVMAX, MKAVMAX at the country level and wxct<sub>=1</sub>, wmd<sub>t=1</sub>, and WAP<sub>t=1</sub> at the global level. | |||
XKAVE and MKAVE are moving average values of export and import propensity, respectively. They are specified as the ratio of agricultural exports and imports to a base value (xbase) for each commodity. For exports, this is basically the sum of production and demand for that commodity; for imports, it is just demand. | |||
[[File:]] | |||
[[File:]] | |||
XKAVMAX and MKAVMAX are maximum values of XKAVE and MKAVE. For crops and meat, XKAVMAX is set to 1.1 times XKAVE, but is not allowed to exceed a value of 0.7; MKAVMAX is set to 1.5 times XKAVE, but also is not allowed to exceed a value of 0.7. For fish, XKAVMAX is set to 1.1 times XKAVE, with a bound of 0.95; MKAVE is set to 1.5 times MKAVE, with a bound of 2. These values are held constant for all future years. | |||
XPriceTermLag, and MPriceTermLag are set to 0 for all commodities. wxc and wmd are the total world agricultural exports and imports; these are set to a value of 1 in the first year. WAP is the initial world price index for each commodity, which is set to 100. | |||
In the forecast years, the process for determining agricultural imports and exports involves the following steps: | |||
#Estimating the agricultural export capacity and agricultural import demand for each country. | |||
#Reconciling the differences between global agricultural export capacity and global agricultural import demand. | |||
#Computing the actual levels of agricultural exports and agricultural imports for each country | |||
The agricultural export capacity is estimated by multiplying the export propensity (XKAVE) by the current year’s production and demand. It is also limited by XKAVMAX: | |||
[[File:]] | |||
Similarly, the agricultural import demand is estimated by multiplying the import propensity (MKAVE) by the current year’s demand, with a limit set by MKAVMAX | |||
[[File:]] | |||
For each country, values are also estimated for its net surplus or deficit (surpdef) for each commodity. This is based on the following factors: 1) post-loss production, 2) domestic demand, 3) the difference between current and desired stocks, and 4) a trade term | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
The first three factors are straightforward. Production minus demand reflects a basic net surplus, which is then adjusted by any net surplus in stocks. The TradeTerm is related the relative role a country plays in global imports and exports and is given as: | |||
[[File:]] | |||
The TradeTerm is positive (negative) when a country has a larger (smaller) share of the global imports than it does of the global exports of a particular commodity and vice versa. Since the TradeTerm is added to surpdef, it acts as a balancing mechanism; countries that appear as relatively larger (smaller) importers get a positive (negative) boost to their estimated net surplus, which tends to reduce (increase) imports as shown below. | |||
At this point, the global sum of exports and imports across countries will likely differ. Therefore, a procedure is required to balance these. In preparation for this one more global variable and several country-level variables are calculated. The global variable is globalsurdefrate, which is the ratio of the sum across countries of net surplus divided by the sum across countries of demand and production, which is the stock base. | |||
[[File:]] | |||
The country-level variables are as follows: | |||
The first term modifies the country’s net surplus, increasing (decreasing) it when the global net surplus is negative (positive). | |||
| |||
[[File:]] | |||
| |||
The second term modifies how rapidly the net surplus is closed. | |||
| |||
[[File:]] | |||
| |||
The third term is simply the ratio of exports to the sum of imports and exports. | |||
| |||
[[File:]] | |||
| |||
The next step is to calculate whether it is necessary to increase (decrease) imports and decrease (increase) exports for each country, and by how much. Whether a country needs to increase its initial estimates of imports and decrease its initial estimates of exports, or vice versa, is determined by the sign of countryextrasurdef. If this value is negative, i.e., the country has a net deficit, it will need to reduce exports and increase imports. The opposite holds for when countryextrasurdef is positive. | |||
As for the amount by which imports and exports need to be increased or decreased, this is a function, in general, of the size of the necessary adjustment and the export share: | |||
[[File:]] | |||
| |||
[[File:]] | |||
Note that the sign of countryextrasurdef and the fact that exportshare is a value between 0 and 1 ensure that when exports increases, imports fall, and vice versa.[[#_ftn9|[9]]] Finally, in this adjustment process, exports and imports are not allowed to fall by more than half or more than double. | |||
This process may not fully reconcile global trade, so a final adjustment is made by setting world trade (WT) as the average of global exports and imports and then adjusting the country values accordingly: | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
IFs can now update the moving average export (XKAVE) and import (MKAVE) propensities for the next time step. The weights given to history are set by the global parameters '''''xhw''''' and '''''mhw'''''. For small exporters, i.e., where exports are less than one tenth of the sum of production and demand, '''''xhw''''' is reduced by 40 percent, allowing for faster adjustment. XKAVE and MKAVE are updated as | |||
[[File:]] | |||
[[File:]] | |||
For crops, the import propensity is bound from below by a factor given by potential GDP (GDPPOT), demand (AGDEM), the conversion factor between agricultural imports in physical terms and dollar values (msf, see section on links to the economic model), and the initial world price for agriculture (WAP). | |||
[[File:]] | |||
Finally, XKAVE and MKAVE are bound from above by XKAVMAX and MKAVMAX, respectively. | |||
== [[3.4Stocks]] == | |||
==== '''First year''' ==== | |||
Due to a lack of good historical data, in the first year, stocks for all three agricultural commodities are assumed to equal desired stocks. These are set to a fraction (''agdstl) ''of total production (AGP) and demand (AGDEM) for each commodity. | |||
[[File:]] | |||
Where | |||
Agdstl is a parameter used to set desired stock levels for agricultural commodities. It is set to be 1.5 times '''''dstl''''', which is a global parameter that can be adjusted by the user | |||
==== '''Forecast years''' ==== | |||
In future years, basic stock levels (CumStk) increase with production (AGP), decrease with demand or consumption (AGDEM), and adjust for net imports (AGM-AGX). | |||
[[File:]] | |||
[[File:]] ) | |||
Of course, the actual stock values (FSTOCK) are not allowed to go negative. If the basic stock level is negative, stocks are set at zero and a shortage (Sho) exists, which affects calorie availability. If the basic stock level is positive there is no shortage and stocks equal the basic level. | |||
[[File:]] | |||
[[File:]] | |||
Also, if shortages are greater than 0, a reduction factor (ReductionFactor''''')''''' is computed which is then used to adjust demand and losses. | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
| |||
== [[3.5 Calorie Availability]] == | |||
Daily per capita calorie availability (CLPC) is initialized in the pre-processor. Where available, data is taken from the FAO[[#_ftn10|[10]]] It is multiplied by population (POP) to yield total daily calorie availability and brought into the model with the name CLAVAL. We already saw that this first year value is used in the calculation of two country-specific factors: 1) calactpredrat, which is a shift factor determined as the ratio of calorie availability to predicted calorie demand in the first year, and 2) sclavf, which is a conversion factor relating the total annual demand for food crops and crop equivalents from meat to daily calorie availability. | |||
In the forecast years, CLAVAL is calculated using the final value of calories per capita. | |||
[[File:]] | |||
Calorie availability combines with regional calorie need in the population model for the calculation of possible starvation deaths (a seldom used variable because in official death statistics people do not die of starvation but rather of diseases associated with undernutrition); the population and health models therefore look instead to the impact of calorie availability on undernutrition and health. | |||
== [[3.6 Prices]] == | |||
IFs keeps track of both national (FPRI) and world (WAP) price indices for each of the three agricultural commodities. All of these are set to an index value of 100 in the building of the base. | |||
The national crop price indices (FPRI, category (1) respond to: 1) changes in global costs of crop production, the latter being expressed as the ratio of global accumulated capital investment in crops to global production and 2) changes in the level of domestic crop stocks. The first factor should provide a long-term basis for rising or falling prices tied to changing technology and other factors of production; the second factor generally should represent shorter-term market variations from that long-term level. | |||
The impact of global costs is given by dividing the ratio of global investment in crops to global production (wkagagpr) in the current year to that same ratio in the first year. The effect of stocks on crop prices (Mul) is calculated using the same ADJSTR function introduced in the description of crop supply, which considers the difference between both the current crop stocks and a desired vale and between current crop stocks and those in the previous year. Two parameters control the degree to which these two ‘differences’ affect the calculation of the adjustment factor. In this case, these are the global, user-controllable parameters '''''fpricr1''''' and '''''fpricr2'''''. All together the equation for domestic crop price indices in the coming year is given as | |||
[[File:]] | |||
The domestic crop price indices are also bound between 0.01 and 1000. | |||
The national meat price indices are linked the global crop price. Specifically, they are given as a moving average of the global crop price index | |||
[[File:]] | |||
Where | |||
'''''fprihw''''' is a global parameter used to control the speed at which the domestic meat price changes. | |||
The national fish price indices are all set equal to the global fish price index. The determination of the global fish price is similar to that for the national crop price, but here the stock of interest is the global stock and there is no effect related to costs. The ADJSTR function is used once again to calculate the adjustment factor (MUL), this time focusing on the desired global fish stock, the difference between this and the current global fish stock, and the change in the global fish stock in the past year. Again, two parameters control the degree to which these two "differences" affect the calculation of the adjustment factor. In this case, these are the global, user-controllable parameters '''''fprim1''''' and '''''fprim2'''''. The global and national fish prices are thus calculated as | |||
[[File:]] | |||
The world price indices for crops and meat are computed, in the following year, as a weighted average of the domestic prices, with the weights given by crop and meat production: | |||
[[File:]] | |||
== [[3.6 Returns and Profits]] == | |||
IFs estimates the net returns in agriculture (AGReturn) for each commodity as the ratio of gross returns (GReturn) to production costs (ProdCost and MProdCost). The agricultural profit ratios (FPROFITR) are then estimated as the ratio of AGReturn in the current year to its value in the initial year. At some points in the evolution of IFs we have used FPROFITR as a guide to rates of investment (see the calculation of mulrprof in All but First 2: Investment); the current formulation for investment does not do so. For completeness, however, we provide a description of these processes in the model, as they still exist as live code. | |||
==== '''Pre-processor and first year''' ==== | |||
In the first year, values for FPROFITR, sfprofitr, and FPRofitR are all set to 1. | |||
==== '''Forecast years''' ==== | |||
The production costs for crops are estimated as the cost of cropland, priced at the cost of new land development (CLD), plus the investment in agricultural capital (KAG). The net revenues are given as total yield times the domestic crop price index. This results in | |||
[[File:]] | |||
[[File:]] | |||
For meat, production costs are estimated by the value of the crop equivalents produced by grazing and the cost of feed, where the value is given by the domestic meat price index. The net revenues are based on the size of the herd and the domestic meat price index. This results in | |||
[[File:]] | |||
[[File:]] | |||
For fish, the production costs are simply estimated by the total production of fish times the domestic meat price index. The net revenues are given as the total production of fish times the domestic fish price index. This implies | |||
[[File:]] | |||
[[File:]] | |||
The net returns for each commodity can then be calculated as | |||
[[File:]] | |||
These net returns are used to account for changes in profits over time, using the variable FPROFITR, which influences investment in agriculture. This variable is calculated for each commodity as | |||
[[File:]] | |||
A similar variable (wfprofitr) is calculated at the global level as a production weighted average of country/region values, but only for crops. | |||
== [[|<u>3.7 Investment</u>]] == | |||
Investment in agriculture is relatively complex in IFs, because changes in investment are the key factor that allows us to clear the agricultural market in the long term. It is very similar to investment in energy, except that we do not need to compute type-specific investments—capital in agriculture is only used for the production function of crops. | |||
We calculate a total agricultural investment need (INAG) to take to the economic model and place into the computation for investment among sectors. This calculation involves multiple factors. These begin with an initial estimate or targeted level of investment (TInAg) that is the product of the ratio of investment to GDP in the previous year times the GDP in the current year. | |||
Three factors modify that basic or target investment level. Two of those are global and one is regional. The first global factor is a multiplier linked to year-to-year change in the ratio of agricultural demand to GDP (WAgDemRMul); typically agricultural demand grows more slowly than GDP. The second is a multiplier responsive to the level of global stocks (MulWSt); if those drop below target levels it would increase production globally and vice versa. The model could use a global price average instead of stocks, but in the recursive structure stocks determine prices and therefore use of stocks accelerates responsiveness of investment. Similarly, the regional factor represents a multiplier tied to regional stock levels (MulSt). | |||
[[File:]] | |||
where | |||
[[File:]] | |||
To elaborate, MulWSt and MulSt are adjustment factors related to global and domestic crop stocks, respectively. Both use the PID ADJSTR function described earlier, just as changes in prices use it in order to set prices that change year-to-year so as to chase supply-demand equilibration over time. For MulWSt, the controlling parameters in the PID function for stocks versus targets and changes in stocks are hard coded with values of -0.3 and -0.9, respectively. For MulSt, these parameters are hard coded with values of -0.2 and -0.4, respectively. | |||
Experience with that initial estimate, however, shows that it can be overly responsive to one or more of the multiplicative adjustment factors, thereby setting up behavior that oscillates. Therefore the next step is to compute a smoothed rate of investment as a share of GDP (SmInAgR). That rate gives more weight (60 percent) to the final investment rate in the previous year than it does to the rate that results from the initial target investment calculation. The overall result of this process is to smooth changes in the rate of investment over time. Desired investment (INAG) is the product of that smoothed rate and GDP. | |||
[[File:]] | |||
where | |||
[[File:]] ) | |||
To further prevent too rapid of a shift in demand for agricultural investment, INAG is not allowed to increase by more than 30 percent or decrease by more than 25 percent from the actual investment in the current year. A second check ensures that the demand is no less than 0.5 percent and no greater than 40 percent of current agricultural capital (KAG). | |||
At this point a user-controlled country-specific multiplier '''''aginvm''''' can boost or reduce INAG. One final check ensures that as long as GDP in the country is larger than it was in the first year, the demand for agricultural investment is not allowed to decline at an annual rate of more than 1 percent per year from the first year. | |||
Investment need (INAG) then enters the economic model, which returns a value reconciled with all other investment needs and that feeds into further calculations in the agriculture model. | |||
| |||
== [[3.8 Economic Linkages]] == | |||
Several variables, such as gross production, stocks, consumer spending, trade, prices and investment, are common to both the economic model and the two physical models. But hardly ever will the economic and physical models produce identical values, even during the first time step when both utilize "data." Thus, although we want the physical model value to override that of the economic model, it cannot simply replace it. Instead IFs extensively uses a procedure of computing an adjustment coefficient during the first time step. That coefficient is the ratio of the value in the economic model to the value in the physical model. In subsequent years IFs uses that coefficient to adjust the value from the physical model before its introduction into the economic model. | |||
Gross production (ZS) in the agricultural sector illustrates this procedure. The value of gross production in the agricultural model is the sum of the products of agricultural production (AGP) and prices (WAP) in each agricultural category. Multiplying that times an adjustment factor (ZSF) computed in the first time stop to assure inter-model consistency produces gross production for the economic (ZS). World average prices (WAP) are used in all the economic/physical model conversions because they assure that global sums (e.g. of exports and imports) will balance.[[#_ftn11|[11]]] | |||
[[File:]] | |||
''Where'' | |||
[[File:]] | |||
Similarly, food stocks in each category (FSTOCK) and an adjustment factor (FSF) produce stocks (ST) for the economic model. | |||
[[File:]] | |||
''Where'' | |||
[[File:]] | |||
A similar translation is made for consumer spending on agricultural commodities, recognizing that not all crop demand is directly by consumers. | |||
[[File:]] | |||
''Where'' | |||
[[File:]] | |||
In the same fashion exports (AGX) and imports (AGM) from the agricultural model allow calculation of exports (XS) and imports (MS) for the economic model. | |||
[[File:]] | |||
''Where'' | |||
[[File:]] | |||
and | |||
[[File:]] | |||
''where'' | |||
[[File:]] | |||
A check and, if necessary, adjustment is made ensure that the monetary values of imports and exports match up at the global level. | |||
[[File:]] | |||
and | |||
[[File:]] | |||
| |||
With respect to prices, the agriculture model passes to the economic model a value (PRI), which reflects the ratio of the current domestic crop price index to the initial world crop price index. | |||
[[File:]] | |||
Finally, investment need (INAG) is passed to the economic model under the variable name IDS, category 1 (agriculture). | |||
== [[3.9 Capital Dynamics]] == | |||
The economic model of IFs returns a (potentially) modified value of IDS, category 1, reflecting the total amount of capital available for agriculture. This value is assigned to the variable IAval, which overrides the value of INAG calculated earlier (earlier it was basically investment demand; after return from the economic model it becomes investment supply).[[#_ftn12|[12]]] The agriculture model divides the investment available for agriculture (IAval) into investment for cropland development and investment for other agriculture capital. The coefficient IALK indicates the portion going to cropland development. | |||
IALK is set to a default value of 0.25 for all countries in the pre-processor. In forecast years, IALK changes from this initial value depending on change in the ratio of return on land (RETR) to return on capital (RETK). | |||
IFs calculates the return rate on land as the crop yield (YL) in the first year divided by the current cost of developing a unit of cropland (CLD). | |||
[[File:]] | |||
The return on capital depends on the difference between the hypothetical level of crop yield (HYL) that could be obtained from an additional unit investment in agricultural capital and the crop yield without that increment (CompYl). Recalling how crop yield is estimated, the hypothetical crop yield is given as | |||
[[File:]] | |||
[[File:]] | |||
and the return on capital is given as | |||
[[File:]] | |||
The ratio of the return to land to the return to capital (RETRAT) is given as | |||
[[File:]] | |||
The adjustment of IALK uses the same first and second order adjustment mechanism that we have seen before with the ADJSTR function. Here the ‘target’ level is the ratio of the return to land to the return to capital in the first year. | |||
[[File:]] | |||
''Where'' | |||
'''''eliasp1''''' and '''''eliasp2''''' are global parameters | |||
Two final checks are made on the value of IALK. First, it is not allowed to exceed a value related to the cost of replacing depreciated investment in land and bringing a portion of grazing or forested land into production. | |||
[[File:]] | |||
Second, IALK is bound between 0.1 and 0.8. | |||
Finally the model updates agricultural capital (KAG) for the next year by subtracting depreciation as represented by agricultural capital lifetime ('''''lks'''''), adding the residual (non-land) investment, and adjusting for any civilian damage from warfare (CIVDM – see international politics model documentation). | |||
[[File:]] | |||
| |||
== [[3.10 Land Dynamics]] == | |||
Land in IFs is divided into five categories—crop, grazing, forest, urban, and other land. Historical data on total land area (LDTot), crop land (LD<sub>l=1</sub>), grazing land (LD<sub>l=2</sub>), forest land (LD<sub>l=3</sub>), and other land (LD<sub>l=4</sub>) are taken from FAO data. Historical data on urban land (LD<sub>l=5</sub>) is taken from WRI. | |||
==== '''Pre-processor and first year''' ==== | |||
A few adjustments to the historical data are made in the pre-processor. | |||
*In the pre-processor total production of food is reconciled with the total trade. In cases where, demand is greater than domestic supply of crops, crop production is increased to reconcile demand with supply of food production. Crop land is also increased proportionately. | |||
*If urban land is more than three quarters the area of other land, land is shifted from urban to other land | |||
*If no data is available for crop land, the same is set to 30 percent of total land area. If no data is available for grazing land, same is set to 5 percent of total land area. If no data is available for other land, same is set to 30 percent of total land area. | |||
After these changes, total land area is recomputed as the sum of the area of the individual land categories. | |||
The pre-processor also reads in a value for potentially arable land ('''''landarablepot'''''), which affects the amount of potential cropland in the model. The share of agricultural capital going to land (IALK) is set to 0.25 in the pre-processor. | |||
One final parameter is estimated related to land in the pre-processor. This is the target rate of growth of cropland ('''''tgrld'''''). When data is available, this is currently estimated as the growth rate of cropland between the year 2015 and the year 2005. | |||
[[File:]] | |||
When no data are available for cropland in either 2015 or 2005, the target rate of growth of cropland is estimated as a function of average income | |||
[[File:]] | |||
with a maximum growth rate given as a function of cropland as a share of total land | |||
[[File:]] ) | |||
Finally, this target growth rate is restricted to fall between -0.003 and +0.01. | |||
In the first year, IFs estimates an initial unit cost of cropland development (CLD) as | |||
[[File:]] | |||
''where'' | |||
IDS is the total investment in agriculture | |||
IALK is the share of agricultural investment going to cropland development | |||
'''''dkl''''' is a global parameter indicating the depreciation rate of investment in cropland, essentially a maintenance cost for existing cropland | |||
'''''tgrld''''' is the target growth rate for cropland | |||
A related factor (SCLdF), to be used in determining the cost of land development in future years, is also calculated in the first year | |||
[[File:]] | |||
==== '''Forecast years''' ==== | |||
IFs calculates changes in land use for the coming year as a result of four key dynamic processes. First, changes in urban land may result from income and population changes. Second, economic shifts related to investment, particularly in the agricultural sector, can affect the amount of cropland. Third, IFs there can be expansion or retirement of grazing land for undefined reasons. Finally, in certain scenarios, specific changes in forest land can result from policies related to issues such as conservation and environmental protection. | |||
=== [[3.10.1 Changes in urban land from income and population changes]] === | |||
Changes in urban land result from changes in population and income. IFs first estimates a predicted level of urban land (LandUrbanPred), which is then compared to current urban land. Any changes are assumed to affect all other land types proportionately, unless this leads to not enough land in a particular category. The growth with income is based on an estimated relationship between income and urban land per capita (LandUrbanR) | |||
The predicted level of urban land (LandUrbanPred) is then given as | |||
[[File:]] | |||
The change in urban land (NUrbLD) is then calculated as | |||
[[File:]] | |||
Limits are placed on the change in urban land area. First, if urban land is growing, the amount of increase in a single year cannot exceed 1/100<sup>th</sup> of a variable that is related to the change in the non-urban share of all other land from the base year (NonUrbanShrR) | |||
[[File:]] | |||
''where'' | |||
[[File:]] | |||
| |||
Second, if urban land is declining, it is not permitted to fall below 10,000 hectares. Third, the changes in Urban land are assumed to affect all other land categories proportionately | |||
[[File:]] | |||
However, this is not allowed to result in the area for a given land category falling below 1,000 hectares. Thus, there may be a slight reduction in the amount of new urban land in certain cases. | |||
=== [[3.10.2 Changes in cropland due to investment and/or depreciation.]] === | |||
The changes in cropland are driven by the economics of land. Specifically, they are a function of the profitability of cropland. Also, they are assumed to affect, at least directly, only the forest and the other land categories. | |||
A maximum amount of cropland expansion each year (MaxLandExpansion) is fixed by the amount of forest land, the amount of other lands, the amount of potential arable land, and the existing amount of cropland. The maximum amount of expansion must be at least 2/100<sup>th</sup> of the existing cropland, but beyond that it cannot exceed either the total amount of forest and other land or the difference between 110% of the potential arable land (landarablepot) and current cropland. | |||
The change in the amount of cropland and the initially estimated share of agricultural investment going to cropland in the following year are computed differently depending upon the maximum amount of cropland expansion relative to the amount of existing cropland and the current level of average income in a country. Specifically, if the maximum amount of cropland expansion is less than 10 percent of existing cropland then it is assumed that there is no change in cropland (lddev = 0) and that no agricultural investment is targeted for cropland development (IALK = 0). | |||
If the condition mentioned in the previous paragraph is met, i.e., there is an ‘adequate’ amount of land for expanding cropland, the amount of change in cropland (lddev) is initially calculated as | |||
[[File:]] | |||
''where'' | |||
IAval is the total amount of funds available for investment in agriculture which is equal to IDS | |||
IALK is the share of agricultural investment going to cropland development | |||
CLD is the unit cost of cropland development | |||
'''''dkl''''' is the depreciation rate of investment in cropland (essential a maintenance cost for existing cropland) | |||
'''''ldcropm''''' is a country-specific multiplier that can be used to increase or decrease changes in cropland | |||
Note that this equation takes into account the need to maintain existing cropland. Also, at this point, the value of LdDev is bound from below to ensure that it does not imply a greater than 10 percent decrease in existing cropland. For relatively poor countries (GDPPCP < 10), the constraint is even stricter. Specifically, IFs calls for a shift in funds to ensure that no cropland is lost. The desired shift in funds is given as | |||
[[File:]] | |||
The actual shift in funds is limited to 90 percent of the available funds, however, where the available funds are the investment in agriculture not initially designated for cropland development | |||
[[File:]] | |||
The value of lddev given the actual shift in funds is given as | |||
[[File:]] | |||
In addition, the share of investment in agriculture designated for cropland development is updated to be[[#_ftn13|[13]]] | |||
[[File:]] | |||
The changes in cropland are linked to changes in land in the forest and ‘other’ categories. The amount coming from/going to forests reflects the share of forest land relative to ‘other’ land, as well as the current level of development. For countries with a GDP per capita higher than 15,000 dollars and where LdDev is less than 0, more is given back to forest land and the ForShrPar is set to 0.25. | |||
| |||
[[File:]] | |||
''where'' | |||
[[File:]]<br/>ForShrPar is given by the function depicted below | |||
The solid line holds when land is being converted from forests to cropland (lddev > 0) and the dotted line holds when land is being converted from cropland to forests (LdDev < 0). In either case, this implies that the less of the change is related to forest land than would be expected by its share. | |||
Two other qualifiers are that the changes in forest land (LDDEVFor) and the changes in ‘other’ land cannot exceed 90 percent of existing land in these categories and the shifts cannot result in either land category falling below 1,000 hectares. These limits feedback to the change in cropland, finally resulting in the following | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
Turning back to the future cost of cropland development, this is estimated differently based only on whether there is ‘adequate’ room for cropland land expansion, defined as when the maximum amount of cropland expansion is greater than 10 percent of existing cropland. If this is the case, the future price of cropland is estimated as | |||
[[File:]] | |||
''where'' | |||
RemRat is the ratio of the maximum land for expansion in the first year to the maximum land for expansion in the current year, with a maximum value of 10 | |||
[[File:]] | |||
This basically states that the price of cropland development grows linearly with growth in cropland and exponentially with declines in available land for cropland expansion. | |||
Alternatively, if the maximum amount of cropland expansion in a given year is less than or equal to10 percent of existing cropland, the cost of bringing new land under cultivation is assumed to grow at the maximum of either 2 percent per year from the cost in the first year or the growth of cropland from the first year. Furthermore, it is not allowed to decline. Thus | |||
[[File:]] | |||
=== [[3.10.3 Changes in grazing land]] === | |||
IFs assumes that relatively poor countries (GDPPCP < 10) will continue to develop additional grazing land, whereas relatively rich countries (GDPPCP > 15) will retire grazing land. No change is expected in countries with average income between $10,000 and $15,000. The annual expansion of grazing land in poor countries is initially estimated as 0.5 percent of the amount of grazing land in the first year. The retirement of grazing land in richer countries is initially estimated as 0.2 percent of current grazing land. | |||
As with cropland, any changes in grazing land will be compensated by changes in forest and ‘other’ land. Each category is initially assumed to be affected proportionately, e.g., | |||
[[File:]] | |||
Unlike the case for changes in cropland, there is no adjustment to the forest share as a function of income or the direction of change in grazing land. As with the changes in cropland, however, the changes in forest and ‘other’ land cannot exceed 90 percent of existing land in these categories and the shifts cannot result in either land category falling below 1,000 hectares. Again, these limits feed back to the change in grazing land. | |||
=== [[3.10.4 Change in forest land due to a policy choice]] === | |||
The model user can also force the land in forest area to increase or decrease at the expense of crop and grazing land via a forest multiplier '''''forestm'''''. The change in forestland, LDSHIFT, is bound. In the case of an increase, i.e., '''''forestm''''' > 1, the amount of added land is limited to 20 percent of crop and grazing land; in the case of a decrease, i.e., '''''forestm''''' < 1, the amount of forest land removed is limited to 20 percent of existing forest land. | |||
[[File:]] | |||
[[File:]] | |||
The amount of land taken from cropland and grazing land is proportional to the amount of each. | |||
[[File:]] | |||
[[File:]] | |||
[[File:]] | |||
=== [[3.10.5 Final checks and renormalization of land use]] === | |||
Two final adjustments are made to the land area values to clean up any quirks that might have be introduced in the previous processes. First, the values for each category are bound between one thousand and ten billion hectares. Second, the values are normalized so that the sum of the categories equals the total amount of land. | |||
[[File:]] | |||
Finally, a value for world forest area (WFORST) is calculated at the end of this process by summing forestland area across all countries. | |||
[[File:]] | |||
| |||
== [[3.11 Livestock Dynamics]] == | |||
In addition to capital and land, the other "stock" or "level" variable with important temporal dynamics is the livestock herd (LVHERD). | |||
==== '''Pre-processor and first year''' ==== | |||
In the pre-processor, as explained earlier, the values for total meat production and animal meat production are initialized. From these values, IFs calculates the value for livestock by dividing the total animal meat by the slaughter rate ('''''slr''''') | |||
==== '''Forecast years''' ==== | |||
The value of LVHERD is calculated by using pre-production loss meat production (AGPppl), adjusting the same for animal products produced (AGPMILKEGGS). This gives total animal meat production. The animal meat production is then divided by the slaughter rate '''''slr'''''[[#_ftn14|[14]]]'''''.''''' | |||
[[File:]] | |||
| |||
== [[3.12 Water Dynamics]] == | |||
Water use begins with data on total water withdrawals from FAO Aquastat. These are divided by the size of the population to get an estimate of water use per capita. | |||
In future years, water use per capita is forecast to increase in parallel with crop production per capita. Specifically, an expected level of water use per capita as a function of crop production per capita (see figure below) is calculated for crop production in the current year (CropPC) and crop production in the first year (CropPCI). The ratio of these values is multiplied by the water use per capita in the first year (WatUsePCI) to get water use per capita in the current year (WatUsePC). This is multiplied by population (POP) to get total water use (WATUSE) | |||
[[File:]] | |||
[[File:]] | |||
| |||
[[File:]] | |||
{| cellpadding="0" cellspacing="0" width="100%" | |||
|- | |||
| <div> | |||
Figure 19: Relationship between water use per capita and Crops production | |||
</div> | |||
|} | |||
<br/><div><br/></div></div></div> | |||
[[File:]] | |||
<div><br/> | |||
---- | |||
<div id="ftn1"> | |||
</div><div id="ftn2"> | |||
| |||
</div></div> | |||
Revision as of 05:47, 20 August 2017
The most recent and complete agriculture model documentation is available on Pardee's website. Although the text in this interactive system is, for some IFs models, often significantly out of date, you may still find the basic description useful to you.
The IFs agricultural model tracks the supply and demand, including imports, exports, and prices, of three agricultural commodities: crops, meat, and fish. Crops, meat and fish have direct food, animal feed, industrial and food manufacturing uses. The agricultural model is also where land use dynamics and water use are tracked in IFs, as these are key resources for the agricultural sector.
The structure of the agriculture model is very much like that of the economic model. It combines a growth process with a partial economic equilibrium process using stocks and prices to seek a balance between the demand and supply sides. As in the economic model, no effort is made in the standard adjustment mechanism to obtain a precise equilibrium in any time step. Instead stocks serve as a temporary buffer and the model chases equilibrium over time.
The most important linkages between the agriculture model and other models within IFs are with the economic model. The economic model provides forecasts of average income levels, labor supply, total consumer spending, and agricultural investment, all of which are used in the agriculture model. In turn, the agriculture model provides forecasts on agricultural production, imports, exports, and demand for investment, which override the sectoral computations in the economic model. The agricultural model also has important links to the population and health models, using population forecasts and providing forecasts of calorie availability.
Dominant Relations
Agricultural production is a function of the availability of resources, e.g. land, livestock, capital, and labor, as well as climate factors and technology. Technology is most directly seen in the changing productivity of land in terms of crop yields, and in the production of meat relative to the input level of feed grain. The model also accounts for lost production (such as spoilage in the fields or in the first stages of the food supply chain), distribution and transformation losses and consumption losses (which account for food lost at the household levels) which are all determined by average income.
Agricultural demand depends on average incomes, prices, and a number of other factors. For example, changing diets can affect the demand for meat, which in turn affects the demand for feed crops. The industrial demand for crops, some of which is directed to the production of biofuels, is also affected by energy prices.
Production and demand, along with existing and desired stocks and historical trade patterns determine the trade in agricultural products. The differences in the supply of crops, meat, and fish (production after accounting for losses and trade) and the demand for these commodities are reflected in shifts in agricultural stocks. Stock shortages feed forward to actual consumption, which is addressed in the population model of IFs. Stocks, particularly changes in stocks, are a key driver of changes in crop prices. Crop prices are also influenced by the returns to agricultural investment and therefore to the basic underlying cost structure. Meat prices are tied to, and track world crop prices, while changes in fish prices are driven by changes in fish stocks.
Stocks and stock changes also play a role, along with general economic and agricultural demand growth, in driving the demand for agricultural investment. The actual levels of investment are finalized in the economic model of IFs and subject to constraints there. The investment can be of two types – investment for expanding and maintaining cropland (extensification) and investment for increasing crop yields per unit area (intensification). The expected relative rates of return determine the split.
The final key dynamics addressed in the agriculture model relate to land, livestock, and water. The latter of these is very straightforward, driven only by crop production. Changes in livestock are determined by changes in the amount of available grazing land, changes in the demand for meat, and the ability of countries to meet this demand as reflected in changing stocks.
In the IFs model, land is divided into 5 categories: crop land, grazing land, forest land, ’other’ land, and urban or built-up land. First, changes in urban land are driven by changes in average income and population, and draws from all other land types. Second, the investment in cropland development is the primary driver of changes in cropland, with shifts being compensated by changes in forest and "other" land. Third, changes in grazing land are a function of average income, with shifts again being compensated by changes in forest and "other" land. Finally, conservation policies can influence the amount of forest land, with any necessary adjustments coming from crop and grazing land.
Structure and Agent System
System/Subsystem
|
Agriculture
|
Organizing Structure
|
Partial market equilibrium
|
Stocks
|
Capital, labor, accumulated technology, agricultural commodities, land
|
Flows
|
Production, loss, consumption, trade, investment
|
Key Aggregate Relationships (illustrative, not comprehensive)
|
Production function with endogenous technological change Price determination
|
Key Agent-Class Behavioral Relationships (illustrative, not comprehensive)
|
Household crop, meat, and fish consumption Industry crop use Livestock producers crop use |
Flow Charts
Overview
The agriculture model combines a growth process in production with a partial equilibrium process that replaces the agricultural sector in the full-equilibrium economic model unless the user disconnects it. The model represents three agricultural commodities: crop, meat, and fish.
The key equilibrating variables are the stocks of the three commodities. Equilibration works via investment to control capital stock and via prices to control domestic demand.
Specifically, as food stocks rise, investment falls, restraining capital stock and agricultural production, and thus holding down stocks. Also, as stocks rise, prices fall, thereby increasing domestic demand, further holding down stocks. Domestic production and demand also influence imports and exports directly, which further affect stocks.
Agricultural Production
Crop Production
Crop production is most simply a product of the land under cultivation (cropland) and the crop yield per hectare of land. Yield is determined in a Cobb-Douglas type production function, the inputs to which are agricultural capital, labor, and technical change. Technical change is conceptualized as being responsive to price signals, but the model uses food stocks in the computation to enhance control over the temporal dynamics of responsiveness. Specifically, technology responds to the imbalance between desired and actual food stocks globally. In addition there is a direct response of yield change to domestic food stocks that represents not so much technical change as farmer behavior in the fact of market conditions (e.g. planting more intensively). Overall, basic annual yield growth is bound by the maximum of the initial model year's yield growth and an exogenous parameter of maximum growth.
This basic yield function is further subject to a saturation factor that is computed internally to the model̶–investments in increasing yield are subject to diminishing rather than constant returns to scale. Moreover, changes in atmospheric carbon dioxide (CO2) will affect agricultural yields both directly through CO2 and indirectly through changes in temperature and precipitation. Finally, the user can rely on parameters to increase or decrease yield patterns indirectly with a multiplier or to use parameters to control the saturation effect and the direct and indirect effects of CO2 on crop yield.
Meat and Fish Production
Meat and fish production are represented far more simply than crop production. Meat production is simply the product of livestock herd size and the slaughter rate. Meat production includes production of non-meat animal products (eg. Milk and eggs). The herd size changes over time in response to global and domestic meat stocks, as well as changes in the demand for meat and the amount of grazing land.
Fish production has two components: wild catch and aquaculture. The former is based on actual data and an exogenous parameter that allows the user to influence rate of catch. Aquaculture is assumed to continue to grow at a country-specific growth rate; a multiplier can also be used to increase or decrease aquaculture production.
Agricultural Demand
Overview
Agricultural demand is divided into crops, meat, and fish. Crop demand is further divided into industrial, animal feed, and human food demand.
Food demand from crops, meat and fish are responsive to calorie demand, which in turn responds to GDP per capita (as a proxy for income). The division of calorie demand between demand for calories from crops and from meat and fish changes in response also to GDP per capita (increasing with income). Caloric demand is used as the basis to compute food demand through conversion to food demand in terms of grams per capita. The caloric value of demand is also used to compute food demand in terms of proteins per capita.
In addition to food demand, demand for feed, industrial demand for meat, crops and fish and food manufacturing demand are also computed. When all components of agricultural demand are computed, the price of the food elements of it are checked to assure that the total household demand for food does not exceed a high percentage of total country-level household consumption expenditures.
Calorie Demand
Crop use for food and meat demand are both influenced by calorie demand. Total per capita calorie demand is driven by GDP per capita, but can be limited by calorie availability as well as by an exogenous parameter specifying maximum calorie need.
The calculations of demand for meat, fish and food crop determine the ultimate division of calorie sources. There is also a limit to the share of calories that can come from meat. The demand for calories from crops is simply the residual obtained by subtracting the demand for calories from meat and fish from the demand for total calories. Caloric value of demand is used to compute food demand in terms of grams per capita and in terms of proteins per capita. Caloric value of demand is adjusted for elasticities to prices for all three categories namely crops, meat and fish.
The user can manipulate calorie demand through the use of an exogenous calorie multiplier and can reduce undernourishment to 5 percent of the population over time through the usage of two other hunger elimination parameters.
Food Demand for Crops, Meat and Fish
Food demand is driven by the demand for calories. A conversion factor translates calorie demand into food demand in terms of grams per capita. Crop prices and an elasticity affect the resultant food demand. So too does a constraint on the maximum calories per capita and the size of the population.
Industrial Demand
Industrial demand (examples would be textile use of cotton or beverage inputs use of barley) is driven primarily by GDP per capita and population. Another important use in recent years has been for biofuels, and that demand component is responsive to world energy price and an elasticity.
Crop prices also influence total industrial demand for crops. A maximum per capita demand parameter constrains the total and an exogenous multiplier allows users to alter the total.
Feed Demand
The total feed demand for the livestock herd is dependent on the weight of the livestock herd and per unit weight feed requirements. The per unit feed requirements increase with GDP per capita as populations move from meat sources such as chickens to more feed intensive ones such as pork and especially beef. But they also are reduced by change in the efficiency of converting feed to animal weight.
Some of the food requirements of livestock are met by grazing, thereby reducing the feed requirements. The feed equivalent of grazing depends on the amount of grazing land, the productivity of that land (computed in the initial year and highly variable across countries), and grazing intensity (which increases with crop prices).
Finally, the feed demand can be modified directly by an exogenous demand parameter that modifies industrial crop demand. The feed demand for meat and fish are calculated using ratios of the food demand to feed demand which are calculated in the initial years of the model. In addition to industrial demand and feed demand, food manufacturing demand is also calculated in the model on the basis of the food demand for all three categories (meat, crops and fish)
Total Agricultural Demand
Total Agricultural demand is the sum of demand for crops to serve industrial, animal feed, food manufacturing and human food purposes.
Financial Constraint on Food Demand
Total food demand in million metric tons consists of the sum of crop demand, meat demand and food demand and fish demand. It can be, however, that the monetary value of those calculated demands is greater than the financial ability of households to pay for them. When that is the case, the food ,meat and fish demand are proportionately reduced.
Agricultural Investment and Capital
The level of total desired agricultural investment are driven by the rate of past investment as a portion of GDP, changes in global crop demand as a portion of GDP, and global crop stocks relative to desired levels. We have experimented also with tying investment to profit rates in agriculture, thereby linking it also to prices relative to costs. The user can use a multiplier to increase or decrease the desired level of investment. This desired amount of investment is passed to the economic model, where it must ‘compete’ with demands for investments in other sectors. The economic model returns a final investment level for use in agriculture.
Investment in agriculture has two possible targets. The first is capital stock. The second is land. The split between the two destinations is a function of the relative returns to cropland development and agricultural capital, the latter of which is determined by the increased yield that could be expected from an additional unit of agricultural capital.
Land Dynamics
In IFs, land use is divided into 5 categories: cropland, grazing land, forest land, "other" land, and urban or built-up land. Four key dynamics are involved in land use change. First, changes in urban land are driven by changes in average income and population, and draws from all other land types. Second, the investment in cropland development is the primary driver of changes in cropland, but this is also influenced by the cost of developing cropland, the depreciation rate, or maintenance cost, of cropland investment, and a user-controllable multiplier. The costs of developing cropland increase as the amount of cropland increases and, therefore, there is less other land available for conversion. Shifts in cropland are compensated by changes in forest and "other" land. Third, changes in grazing land are a function of average income, with shifts again being compensated by changes in forest and "other" land. Finally, conservation policies can influence the amount of forest land, with any necessary adjustments coming from crop and grazing land.
Agricultural Equations
Overview
Briefly, each year the agriculture model begins by estimating the production (pre- and post-production loss) of crops, meat, and fish. It then turns to the demand for these commodities. This begins with a computation of caloric demand from crops, meat, and fish, which is translated into demand for food going directly to consumers. Other demands for crops, meat, and fish are for feed, industrial uses (e.g. biofuels), and food manufacturing. Losses in the production, distribution and consumption of agricultural commodities are also accounted for. This is followed by computations for trade. The model then considers the balance between the demands and the available supply based on production, imports, and exports. Any excess supply increases stocks. In the case of excess demand, stocks are drawn down; this can result in shortages if there are not enough stocks, which leads to an inability to meet all of the demands. Levels of, and changes in, stocks influence prices for the coming year, as well as desired investment, which are passed to the economic model, which determines the actual amount of investment that will be available. With this knowledge, the model can then estimate values for changes in land development, agricultural capital, and livestock for the coming year.
Agricultural Supply
Crop, meat, and fish supply have very different bases and IFs determines them in separate procedures.
Crop Production
Crop production, pre-loss, (AGPpplf=1) i is the product of total yield and land devoted to crops (LDl=1).
We focus here on the determination of yield; the amount of land devoted to crops is addressed in the sections below.Yield functions are almost invariably some kind of saturating exponential that represents decreasing marginal returns on inputs such as fertilizer or farm machinery. Such functions have been used, for instance in World 3 (Meadows, 1974), SARUM, (SARU, 1977), the Bariloche Model (Herrera, et al., 1976), and AGRIMOD (Levis, et al., 1977). IFs also uses a saturating exponential, but relies on a Cobb-Douglas form. The Cobb-Douglas function is used in part to maintain symmetry with the economic model but more fundamentally to introduce labor as a factor of production. Especially in less developed countries (LDCs) where a rural labor surplus exists, there is little question that labor, and especially labor efficiency improvement, can be an important production factor.
Pre-processor and first year
In the pre-processor, agricultural production is initialized using data from the FAO food balance sheets. For details of the series that are used in this initialization, refer Annex 1 of this document. In the first year of the model, total crop production is calculated by adjusting the initialized value of crop production for production losses, as the FAO data are for post-loss production. Yield (YL) is computed simply as the ratio of total crop production (AGPpplf=1) to cropland (LDl=1). It is bound, however, to be no greater than 100 tons per hectare in any country.
In addition to yield, a number of other values related to production are calculated in the first year of the model that are used in forecast years.
First, a scaling factor cD is calculated in the first year of the model. This is basically the constant in the Cobb-Douglas formulation for estimating yields. It is based upon the base year yield (YL), capital (KAG), and labor supply (LABS). The labor supply is adjusted using a Cobb-Douglass alpha exponent (CDALF) which is explained in detail below. cD is similar to the shift factors elsewhere in the model, which are used to match predicted values in the base year to actual values. It does not change over time. It is computed using the following equation,
Second, a target growth rate in yield is computed (TgrYli) which is used in forecast years to restrict the growth rate of the yield. This target growth is a function of current crop demand (AGDEM), expected crop demand (Etdem), and a target growth rate in cropland.
where
tgrld is a country-specific parameter indicating target growth in crop land
Etdem is an initial year estimate of the sum of industrial, feed and food demand for crops in the following year
Forecast years
In forecast years, IFs computes yield in stages. The first provides a basic yield (byl) representing change in long-term factors such as capital, labor and technology. The second stage uses this basic yield as an input and modifies it based on prices, so as to represent changes in shorter-term factors (e.g. amounts of fertilizer used, even the percentage of land actually under cultivation). Finally, in a third stage, yields are adjusted in response to changing climate conditions.
First stage (Adjustment for long-term factors)
The basic yield (Byl) relates yield to agriculture capital (KAG), agricultural labor (LABS), technological advance (Agtec), a scaling parameter (cD), an exponent (CDALF), and a saturation coefficient (Satk).
[[File:]]
The equations for KAG and LABS are described elsewhere (see sections 3.9 and the economic model, respectively).
- cD is the scaling factor calculated in the first year of the model. Its calculation is described in the section above
- CDALF is the standard Cobb-Douglas alpha reflecting the relative elasticities of yield to capital and labor. It is computed each year in a function, rooted in data on factor shares from the Global Trade and Analysis Project, driven by GDP per capita at PPP.[1]
- Agtec is a factor-neutral technological progress coefficient similar to a multifactor productivity coefficient. It is initially set to 1 and changes each year based upon a technological growth rate (YlGroTech). Its computation is described below.
[[File:]]
- The saturation coefficient Satk is a multiplier of the Cobb-Douglas function and of the technological change element. It is the ratio of the gap between a maximum possible yield (YLLim) and a moving average of yields to the gap between a maximum possible yield and the initial yield, raised to an exogenous yield exponent (ylexp). With positive parameters the form produces decreasing marginal returns.
[[File:]]
where
Sylr is a moving average of byl, the historical component of which is weighted by 1 minus the user-controlled global parameter ylhw.
ylexpis a global parameter
The maximum possible yield (YLLim) is estimated for each country and can change over time. It is calculated as the maximum of 1.5 times the initial yield (YLr,t=1) and the multiple of an external user-controlled parameter (ylmax) and an adjustment factor (YLMaxM).
[[File:]]
where
ylmax is a country-specific parameter
The adjustment factor YLMaxM allows for some additional growth in the yields for poorer countries
[[File:]]
where
DevWeightr is GDPPCPr/30, with a maximum value of 1
YlMaxFound is the maximum value of YL found in the first year
|
Box1: Computation of technological growth rate for yield The algorithmic structure for computing the annual values of YlGroTech involves four elements:
The algorithmic structure this is: [[File:]] |
Second stage of yield calculation (short term factors)
Before moving to the next stage, a check is made to see if the growth in byl is within reason. Specifically, Byl is not allowed to exceed the moving average of Byl (Syl) times a given growth rate (YlGrbound). This bound is the maximum of a user-controlled global parameter - ylmaxgr and an initial country specific target growth rate (Tgrylir).[3]
At this point, the basic yield (byl) is further adjusted by a number of factors. The first of these is a simple country-specific user-controlled multiplier – ylm. This can be used to represent the effects of any number of exogenous factors, such as political/social management (e.g., collectivization of agriculture).
[[File:]]
The basic yield represents the long-term tendency in yield but agricultural production levels are quite responsive to short-term factors such as fertilizer use levels and intensity of cultivation. Those short-term factors under farmer control (therefore excluding weather) depend in turn on prices, or more specifically on the profit (FPROFITR) that the farmer expects. Because of computational sequence, we use domestic food stocks as a proxy for profit level. Note that this adjustment is distinct from the adjustment above where global stocks affect the technological growth rate.
The stock adjustment factor uses the ADJSTR function to calculate an adjustment factor related to the current stocks, the recent change in stocks, and a desired stock level. The desired stock level is given as a fraction (Agdstl) of the sum of crop demand (AGDEMf=1) and crop production (AGPf=1). Agdstl is set to be 1.5 times dstl, which is a global parameter that can be adjusted by the user.
The focus in IFs on yield response to prices differs somewhat from the normal use of price elasticities of supply. For reference, Rosegrant, Agcaoili-Sombila, and Perez (1995: 5) report that price elasticities for crops are quite small, in the range of .05 to .4.
Third stage of yield calculation (Adjustment for a changing climate)
In the third stage, IFs considers the potential effects of a changing climate on crop yields. This is introduced through the variable ENVYLCHG[4] which is calculated in the environmental model. This variable consists of two parts: the direct effect of atmospheric carbon dioxide concentrations and the effects of changes in temperature and precipitation.
[[File:]]
The direct effect of atmospheric carbon dioxide assumes a linear relationship between changes in the atmospheric concentration from a base year of 1990 and the percentage change in crop yields.
[[File:]]
where
envco2fert is a global, user-controllable parameter
CO2PPMt=1990 is hard coded as 354.19 parts per million
The effect of changes in annual average temperature and precipitation are based upon two assumptions: 1) there is an optimal temperature (Topt) for crop growth, with yields falling both below and above this temperature and 2) there is a logarithmic relationship between precipitation and crop yields. The choice of this functional form was informed by work reviewed in Cline (2007). Together, these result in the following equation:
[[File:]]
[[File:]]
where
T0 and P0 are country-specific annual average temperature (degrees C) and precipitation (mm/year) for the period 1980-99.
DeltaT and DeltaP are country specific changes in annual average temperature (degrees C) and precipitation (percent) compared to the period 1980-99. These are tied to global average temperature changes and described in the documentation of the IFs environment model.
Topt is the average annual temperature at which yield is maximized. It is hard coded with a value of 0.602 degrees C.
SigmaTsqd is a shape parameter determining how quickly yields decline when the temperature moves away from the optimum. It is hard coded with a value of 309.809.
CO2Fert and ClimateEffect are multiplied by each other to determine the effect on crop yields.
There are two final checks on crop yields. They are not allowed to be less than one-fifth of the estimate of basic yield (Byl) and they cannot exceed the country-specific maximum (ylmax) or 100 tons per hectare. Finally crop production is adjusted for production losses to arrive at post loss production (AGP). Losses are discussed in detail in section 3.1.4 below
Meat Production
Meat production in IFs is the sum of animal meat production and non-meat animal products (AGPMILKEGGS). Animal meat production in a particular country is a function of the herd size and the slaughter rate and non-animal meat products are calculated by applying a ratio MilkEggstoMeatI which is calculated in the first year of the model as the ratio of non-meat animal production to the meat production. Meat production is then adjusted for production losses which are described in detail in section 3.1.4 below.
[[File:]]
Where,
LVHERD is the size of livestock in a particular country in a particular year
slris the slaughter rate which is a global parameter
AGLOSSPROD is the meat production loss.
Pre-processor and first year
In the pre-processor, meat production is initialized in the model using data from the FAO food balance sheets. Total meat production and animal meat production (which is the sum of bovine meat production, mutton and goat meat production, pig meat production, poultry meat prod, and other meat production) are initialized separately. If data on all of the animal meat sub-categories is unavailable, then Animal meat production is calculated as 30 percent of total meat production. Animal production is also not allowed to exceed 99% of the value of total meat production.
AGPMILKEGGS, which is the non-meat animal production is then calculated as total meat production minus total animal meat production. The non-meat production ratio MilkEggstoMeatI is calculated as the ratio of the initialized value of AGPMILKANDEGGS and meat production in the first year. This is used in forecast years to calculate the value of non-meat animal production, and is held constant over time.
[[File:]]
The size of the livestock (LVHERD) is also computed in the first year using the initialized value of pre-loss meat production. This value of LVHERD is used in forecast years to compute meat production.
[[File:]]
For a detailed discussion on the dynamics of livestock herd, refer to section 3.11 of this document.
Forecast years
Pre-production loss values for meat production are calculated in IFs as meat production (AGPppl) and production of non-meat animal products (AGPMILKANDEGGS). Meat production, in metric tons, is given as the multiple of the herd size (LVHERD) and the slaughter rate (slr). The latter is a global parameter. These values are then adjusted for production losses for meat (AGPRODLOSS) to arrive at post production loss values (AGP). The same meat production loss percentage is also applied to the non-meat production to arrive at post loss production values for the variable. The dynamics of production losses are discussed in section 3.1.4
[[File:]]
Where,
[[File:]]
Production of non-animal meat products is computed using the non-meat production ratio which is applied to the animal meat production.
[[File:]]
The dynamics of the livestock herd are described in section 3.11.
Fish Production
The production of fish has two components, wild catch and aquaculture. Fish caught through aquaculture is treated as a stock in the model and is a function of a growth component. Wild catch on the other hand is treated as a flow in the model.
Pre-processor and first year
Data for fish catch and aquaculture is derived through two main sources, namely the FAO food balance sheets and the FAO Fishstatj software. Data for fish production, imports and exports is initially extracted from the FAO Food Balance Sheets. However, no breakout is available for fish caught as wild catch and fish caught through aquaculture. This bifurcation is available in the dataset from the FAO Fishstatj database. The data from the FAO food balance sheets is broken down into fish catch (AGFISHCATCH) and aquaculture (AQUACUL) using data from the FAO fishstatj dataset.
In the first year, the values for pre-loss production of wild fish, AGFISHCATCHppl and aquaculture, AQUACULppl, are calculated by adding in a level of catch loss, which is not reflected in the FAO and Fishstatj data. Separate parameters, aglossprodpercf=3 and aglossprodpercf=4, are used for wild catch and aquaculture.
Forecast years
The amount of aquaculture (AQUACUL) in forecast years can be modified by the user. Production is assumed to grow over time. The default growth rate in the first year for all countries is 3.5 percent, but this value can be modified by the user, by country, with the parameter aquaculgr. This growth rate declines to 0 over a number of years given by the global parameter aquaculconv. Users can change the amount of aquaculture production, by country, with the multiplier aquaculm[1]. Finally, this is adjusted for production losses from aquaculture with Aquaculloss
[[File:]]
where
aquaculgrr,t declines from aquaculgrr,t=1 to 0 over aquaculconv years
Wild catch is initialized in the pre-processor as the variable AGFISHCATCH. The pre- production loss of wild catch is computed after applying a multiplier fishcatchm and this is adjusted for losses[2] (Catchloss) to arrive at post production loss wild fish catch.
[[File:]]
Total, post-production loss fish production (AGP) is then given as:
[[File:]]
'Losses and waste'
Losses can occur at several places along the chain from production. In earlier sections, we mentioned losses at the production stage. Losses can also occur in the process of transmission and distribution from the producer to the final consumer and at the consumer stage. The latter is sometimes referred to as food waste, but for our purposes, we will use the term loss for all three stages: production, transmission and distribution, and consumption.
The FAO Food Balance Sheets provide data on losses during transmission and distribution, but not at the production or consumption stages. Until we are able to find data showing a clear relationship between these losses and GDP per capita, or some other explanatory factor, we make an assumption of production losses and consumption losses of 10% for all countries. The user can make changes in these values with the parameters aglossprodpercandaglossconspercrespectively. The former can be set for crops, meat, wild catch, and aquaculture separately. The latter combines wild catch and aquaculture as fish, as we do not have separate data on the consumption of wild caught versus farmed fish. More details on the use of these parameters and the actual calculation of production and consumption losses are provided in sections 3.1.1-3.1.3 and 3.2.1, respectively.
Turning to transmission and distribution losses, some agricultural commodities will never make it from the producer to the final consumer because of pests, spoilage, etc. The FAO food balance sheets provide data on food lost to waste for crops and meat , but not for fish. Thus, for now we assume that there are no losses in this stage for fish. For crops and meat, though we were able to establish relationships between transmission and distribution losses and GDP per capita. These are shown in the figures below:
Pre-processor and first year
The initial values for transmission and distribution losses are taken directly from the FAO Food balance sheets. For those countries without data, an assumed loss of 1 ton (0.000001 MMT) is used. These are given by the variable AGLOSSTRANS[[|r, f=1-3]]. As with consumption, wild catch and aquaculture are combined into a single category, fish, as we do not have separate data; also, for the moment the value of AGLOSSTRANSr, f=3 is set to 0 for all countries.
In the first year, a ratio of transmission/distribution loss to food demand, FDEM, is computed as:
Forecast years
In future years, for crops and meat, the initial estimate for transmission and distribution losses are calculated as follows:
· Predictions are made for the ratio of transmission/distribution loss to food demand as a function of GDP per capita (predaglosstrans) for the first year and the current year.
· The ratio of the predicted values for the current year to the predicted value for the first year is multiplied by AgLossTransToFoodRatI.
· That result is multiplied by FDEM for the current year to get losses in MMT.
· That result is multipled by the parameter aglosstransm, to get a final value.
This can be expressed as:
Some further adjustments may be made to AGLOSSTRANS in the process of balancing global trade and balancing domestic supply and demand. These are discussed later in this documentation.
Agricultural Demand
IFs computes demand, or uses, for three agricultural categories—crops, meat, and fish. These commodities are used for direct human consumption (FDEM), animal feed (FEDEM), industrial uses, e.g. biofuels (INDEM), and food processing and manufacturing (FMDEM). IFs also tracks the losses in transmission and distribution (AGLOSSTRANS). Total demand (AGDEM) is the sum of these five use categories and is given in MMT per year.
Section 3.1.4 describes the calculation of AGLOSSTRANS, so that is not repeated here. The calculation of the demand for direct human consumption, FDEM begins with estimates of daily per capita calorie demand for crops, meat, and fish. Briefly, IFs first estimates total per capita calorie demand, which responds to GDP per capita (as a proxy for income). The division of total demand between demand for calories from crops and from meat and fish also changes in response to GDP per capita (more meat and fish demand with increasing income). Finally, the division of calories from meat and fish is calculated based on historic patterns. Using country and commodity specific factors, the daily per capita calorie demands are converted to grams per capita per day and protein per capita per day. The grams per capita per day are then multiplied by the size of the population, POP, and the number of days in a year, 365, to arrive at FDEM.
The other demands, FEDEM, INDEM, and FMDEM are driven by factors such as the size of the livestock herd, LVHERD, and the use of crops for fuel production. In cases where information is lacking, these demands are determined in relation to FDEM. Finally, there may be some modifications to all of the demand categories due to shortages or other factors, as described in the rest of this section.
'''3.2.1 Daily per capita demands – calories, grams, and protein'''
IFs tracks one set of variables for agricultural demands, or uses, on a daily per capita basis. These are. specifically, calories (CLPC), protein (PROTEINPC), and grams (GRAMSPC), for each category – crops, meat, and fish.
Pre-processor and first year
Daily calories per capita (CLPC), by category, are initialized in the IFs pre-processor using data from the FAO food balance sheets. Data on daily protein per capita and grams per capita are also read into the pre-processor.[1] If data are available for crops, meat, and fish, total values for calories, protein, and grams are calculated as sums of the three categories. For countries where no data are available for one or more of the categories, the model follows a set of procedures to fill in the missing data. These procedures uses, among other things, 1) equations that relate total calories per capita per day and the share of these calories from crops versus meat and fish to GDP per capita and 2) other ratios derived from global averages of those countries with data. Later in the pre-processor, CLAVAL, which represent the total calories (across all categories) per day for the population as a whole is also calculated.
The equation for total calories as a function of GDP per capita is stored as "GDP/Capita (PPP 2011) Versus Calorie Demand (fixed-effect)" and is illustrated below.[2]
[[File:]]
Figure 13: Calories per capita vs GDP per capita at PPP
The equation for the share of calories from meat and fish as a function of GDP per capita is stored as " GDP/Capita (PPP 2011) Versus CLPC from MeatandFish (2010) Log"
Both of these are in a logarithmic form, indicating that both total calories and the share of calories from meat and fish increase with GDP per capita, but at a decreasing rate. As the data do not show a clear pattern for the breakdown between meat and fish, which is largely due to cultural patterns and geography, the model uses historical values rather than an estimated equation, as discussed below. In the pre-processor, an average global value is used for countries without data.
In the first year of the model, one of the first things that occurs is a recalculation of GRAMSPC as GRAMSPC = FDEM/(POP * 365) * 100000. This is to ensure the consistency between the daily per capita variable, GRAMSPC, and the annual national value, FDEM. This is necessary because FDEM may have been modified in the pre-processor as part of ensuring a balance between the initial year supply of agricultural produces and their use. This is described in more detail in Box 1.
In addition, a number of additional values related to calories to be used in the forecast period are calculated.
- CalActPredRat: the ratio between actual calories available and the predicted value.[3] It is used as a multiplicative shift factor. The predicted level of is estimated using the equation for total calories per capita as a function of GDP per capita described above. This is bound from above by an assumed maximum value, given by the global parameter calmax. The value of calactpredrat gradually converges to 1 over a period given by the global parameter agconv and appears in future equations with the name AdjustForInitialDevc.
- MeatAndFishActPredRat: the ratio between actual share of calories from meat and fish to the predicted value. It is used as a multiplicative shift factor. The predicted level of is estimated using the equation for share of calories from meat and fish per capita as a function of GDP per capita described above.
- MeatToMeatFishRatI: the ratio between calories from meat and calories from meat and fish. It is used to separate the future estimates of calories from meat and fish into separate values for meat and fish.
- ProtToCalRatI: the ratio of daily per capita protein to daily per capita calories, by category. It is used to convert future estimates of calorie availability to protein availability. If for some reason the initial estimate of ProtToCalRatI is 0 for any category, the median value for that category based on 2010 is used.
- GramsToCalRatI: the ratio of daily per capita grams to daily per capita calories, by category. It is used to convert future estimates of calorie availability to a value in grams, which is then used to estimate aggregate demand for food for direct human consumption. If for some reason the initial estimate of GramsToCalRatI is 0 for any category, the median value for that category based on 2010 is used.
Forecast years
In the forecast years, daily per capita calorie demand begins with a prediction of a total demand, CalPerCap, as a function of average income using the equation above, with a maximum value given by calmax. Two other values are also calculated at this point. First, a base level of calories per capita, CalBase, is also calculated, which is given as the minimum of 3000 or calmax minus 300. Second, because comparative cross sections show a growth of around 7.6 calories per capita per year independent of average income, a factor representing this increase (CaldGr) is calculated as:
[[File:]]
Thus, depending on the exact values of calmax, CalBase, and CalPerCap, CaldGr grows each year by a value that centers around 7.6 calories. This value is then added to the predicted value in calculating the total demand for calories.
The equation also takes into account calmax and the multiplicative shift factor on calories per capita calculated in the first year of the model. The latter is named AdjustForinitialDevc, which, as noted previously, is calculate as the value of calactpredrat gradually converging to 1 over a period given by the global parameter agconv
[[File:]]
Finally, a value for the total calories per day, CalDem, is calculated by multiplying TotalCalPerCap times POP.
The next step is to divide the total calories between crops and meat plus fish. First, a predicted value of the share of total calories going to meat and fish, MeatAndFishPctPred, is calculated as a function of GDP per capita, using the equation described earlier. Second, the ratio of between actual share of calories from meat and fish to the predicted value, MeatAndFishActPredRat, calculated in the first year is potentially modified. Specifically, a new variable, AdjustForInitialDevm, is assigned either the intial value of MeatAndFishActPredRat, or a value that reflects convergence of MeatAndFishActPredRat to a value of 1 over a period given by the global parameter agconv. The countries for which convergence does not occur are the South Asian countries – India, Nepal and Mauritius – which are traditionally low meat consuming countries. The actual share of calories from meat and fish is then calculated as:
[[File:]]
A minimum value of 3.5 percent is also imposed.
With this value for MeatAndFishPctAct, the model can divide the total calories between crops and the combination of meat and fish. Using the value for MeatToMeatFishRatioI, calculated in the first year, the model can then estimate the calories from meat and fish separately. The values are stored in the variable CLPC(r,f)
At this point, these values are adjusted for changes in world food prices and elasticities to demand for these prices.
[[File:]]
where
WAPf=1-3 are the global food prices for crops, meat, and fish
X is the price elasticity of demand and takes on the value of elascd, elasm, and elasfdfor crops, meat, and fish, respectively
Given these adjustments, TotalCalPerCap is recalculated as the sum of CLPC for crops, meat, and fish.
Finally, a parameter clpcm is applied to the final value of calories per capita that allows the user to manipulate demand for calories in addition to two parameters (that allow the user to eliminate hunger in a particular country over time) which are described below.
The parameters malnelimstartyr and malnelimtargetyr allow the user to reduce hunger in any country over a specific period of time. The activation of these parameters by the user, calculates the required cumulative growth rate in calories to eliminate hunger (reduce the undernourished population to 5 percent of the total population) ClPCcum. This cumulative growth rate is calculated using a logarithmic function that computes the growth rate relative to the household income and unskilled labor in a country.[4] Also, the user can activate a switch malelimprecisesw, which calculates the specific number of calories required to eliminate hunger for the most undernourished part of the population. An individual who consumes less than 1000 calories per day but is still alive is assumed to be the most undernourished person in the population.
Therefore the final equation is as follows,
[[File:]]
Where,
clpcm is a multiplier that can be used to affect the demand for calories
ClPCcum is the cumulative growth rate required in calories per capita to eliminate hunger over a specific time period determined by malnelimstartyr and malnelimtargetyr
Caldef is the cumulative number of calories required to eliminate hunger for the most undernourished part of the population. This is calculated through the activation of malelimprecisesw.
At this point, i.e., after dealing with the hunger targets, the values for daily grams per capita (GRAMSPC) and daily protein per capita (PROTEINPC) are calculated by multiplying the values for CLPC by GramsToCalRatI and ProtToCalRatI, respectively. Recall that these values were computed in the first year.
A final adjustment to CLPC, PROTEINPC, and GRAMSPC can occur as a result of shortages. This begins with a reduction in FDEM, as described in Section 3.4: Stocks, which is then translated into new values for GRAMSPC, which are then used to recalculate CLPC and PROTEINPC.
One final variable, CLAVAL, which represent the total calories (across all categories) per day for the population as a whole is then calculated as total calories per capita times the population.
'''3.2.2 Agricultural demand for direct human consumption (FDEM)'''
FDEM represents the amount of agricultural commodities going directly to consumers, presumably for consumption.
Pre-processor and first year
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used for direct human consumption, FDEM. If these data are missing for any commodity, a value is calculated by multiplying the daily grams per capita by the size of the population (POP) and the numbers of days in a year (365), and then divided by 100000 to get the units correct. As noted in Box 1, certain adjustments may be made to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries.
No adjustments are made to FDEM in the first year.
Forecast years
In the forecast years, FDEM is initially calculated based upon the calculation of daily grams per capita described in section 3.2.1:
[[File:]]
There are two situations where the value of FDEM might be adjusted. The first case is where more than 85 percent of consumers’ expenditures are on food stuffs. If this is the case, the values of FDEM for crops and meat and fish are reduced proportionately, as described in section 3.2.5.
The second case is when a country faces absolute shortages, i.e., the total domestic supply, AGDEM, is not adequate to meet all of the demands, FDEM + FEDEM + INDEM + AGLOSSTRANS even after drawing down stocks to 0. Here, each of these demands/uses are reduced proportionately to restore the balance as described in Section 3.4: Stocks. In both cases, the decreases in FDEM are fed forward to reduce the actual calories available, as described in section 3.2.1.
3.2.3 Feed demand for crops, meat and fish
Feed demand, FEDDEM, represents: 1) the amount of crops that are used to complement what livestock receive from grazing, and 2) an unspecified use of meat and fish, which appears in the FAO Food Balance Sheets.
Pre-processor and first year
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used as feed for other agricultural production, usually meat. If data are missing, a minimum value of 1 ton, or .000001 MMT is used.
An initial adjustment to feed demand for crops can occur in the pre-processor. This occurs when the production from grazing land is not being fully utilized. Specifically, this is when the amount of equivalent feed from grazing land, i.e. grazing land productivity, here named GLandCAP, implies a lower than assumed minimum value of 0.01 tons of crop equivalents per hectare, here named MinLDProd. The implied value of GLandCap is calculated as the difference between the total feed requirement for the number of livestock minus the feed demand divided by the amount of grazing land.
[[File:]]
where
LiveHerd is the size of the livestock herd (discussed in section ?)
LDGraz is the amount of grazing land (discussed in section 3.10: Land Dynamics)
FEDDEMr,f=1 is the value for demand for crops for feed
[[File:]]
Fedreq is an estimate of the per animal feed requirements, which is a function of GDP per capita. The function is depicted in the figure below[5]:
Figure 15: Per animal crop feed demand as a function of GDP per capita |
If the value of GLandCAP is less than the minimum, MinLDProd—currently hard coded as 0.01 tons of crop equivalents per hectare, based on values for the Saudi desert), then CFEDDEMr,f=1 is recalculated as the difference between the total feed requirement for the number of livestock minus the amount of feed equivalent produced by grazing using the minimum productivity.
[[File:]]
Note that this occurs when the feed from crops meets most, if not all, of the total feed requirements, implying little or no need for feed equivalents from grazing land. Also a minimum value of 0.01 MMT is set for CFEDDEM.
Finally, as noted in Box 1, certain adjustments may be made in the pre-processor to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries.
In the first year, the model once again checks to make sure that the grazing land productivity exceeds a minimum value and this time stores this value for future use. A parallel equation to that in the pre-processor is used to get an initial estimate for grazing land productivity, now named GldCap:
[[File:]]
where
LVHERDr,t=1 replaces LiveHerd from the equation in the pre-processor
LDr,l=2,t=1 replaces LDGraz from the equation in the pre-processor
FEDDEMr,f=1 replaces CFEDDEMr,f=1 from the equation in the pre-processor
Fedreqr is the same as in the equation in the pre-processor
Now, if the model estimates that GldCAP is below the minimum level, still called MinLDProd and hard coded to a value of 0.01, a new value of GldCAP calculated:
[[File:]]
where
LVHERDr,t=1, LDr,l=2,t=1, FEDDEMr,f=1, and fedreqr are defined as above
fedreqmr is a multiplier required to ensure that the grazing land productivity meets the difference between the total feed requirement and that provided by crops in the initial year. It is calculated as:
[[File:]]
Note that this value is always greater than or equal to 1 given the condition for making the adjustment. When no adjustment is made, fedreqm is set to 1. These values of GldCAP and fedreqm, calculated in the first year, are held constant for all forecast years
Finally, one other value is calculated in the first year – FeedToFoodRatI, which is the ratio between FEDDEM and FDEM. This is calculated for crops, meat, and fish, but is only used for the latter two categories in the forecast years, as described below.
Forecast years
In the forecast years, FEDDEM is calculated as a function of the size of the livestock herd (LVHERD), the feed requirements per unit livestock (fedreq), the amount of grazing land (LDl=2), and the productivity of grazing land (GldCAP), but adjustments are also made reflecting the effect of global crop prices on grazing intensity (WAPf=1), changes in the efficiency with which feed is converted into. meat, and the adjustment factor fedreqm calculated in the first year. There is also a parameter with which the user can cause a brute force increase or decrease in FEDDEM (feddemm)
The model first calculates the amount of crop equivalent produced from grazing land using the following equation:
[[File:]]
where
LDr,l=2 is the amount of grazing land; the dynamics of this variable is discussed in section 3.10: Land Dynamics
GldCAPr is the country value for grazing land capacity initialized in the first year
WAPt,f=1 is global price for crops; and
elglinpr is a global parameter for the elasticity of livestock grazing intensity to annual changes in world crop prices; the basic assumption is that increasing prices should lead to increased grazing intensity and therefore greater productivity of grazing land[6]
This production of crop equivalents from grazing land is then subtracted from total feed requirement in the following equation:
[[File:]]
Where
LVHERD, fedreq, and fedreqm are as previously described. LVHERD and fedreq are updated each year as described in section 3.11: Livestock Dynamics and as a function of GDP per capita, respectively. fedreqm, determined in the first year, does not change over time.
livhdpro is a global parameter related to the rate at which the productivity of crops in producing meat improves over time. This part of the equation implies that the amount of feed needed to produce a unit of meat declines over time to a minimum of half the original amount required
feddemm is a country-specific multiplier that can be used to increase or decrease crop demand for feed purposes
For meat and fish, a simpler process is used. The feed to food ratio, FeedToFoodRatI, calculated in the initial years of the model is used to calculate the share of feed demand for meat and fish respectively.
[[File:]]
Note that there is no multiplier equivalent to feddemm for meat and fish.
Finally, as with FDEM, FEDDEM may be adjusted to account for excessive consumer spending on food, as described in Box 2 or due to shortages in crops, meat, or fish as described in Section 3.4: Stocks.
'''3.2.3 Industrial demand for crops, meat and fish'''
Industrial demand, INDEM, represents the amount of crops, meat, and fish that are used in industrial processes.
Pre-processor and first year
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used in industrial processes. If data are missing, a minimum value of 1 ton, or .000001 MMT is used.
Finally, as noted in Box 1, certain adjustments may be made in the pre-processor to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries.
Figure 18: Per capita industrial demand for crops as a function of GDP per capita |
In the first year, two values related to industrial demand for crops are calculated. The first of these is a multiplicative shift factor (INDEMK), which is calculated as the ratio of actual to predicted industrial demand for crops. The predicted value is given by a function that relates per capita industrial demand to GDP per capita, which is shown [[File:]]
below.[7] This multiplicative shift factor remains constant over time.
As with FEDDEM, one other value is calculated in the first year – IndToFoodRatI, which is the ratio between INDEM and FDEM. This is calculated for crops, meat, and fish, but is only used for the latter two categories in the forecast years, as described below.
Forecast years
In the forecast years, for crops, the initial value of industrial demand is updated using the table function above to get a predicted value for industrial demand per capita, which is then multiplied by population (POP) and the multiplicative shift factor (IndemK). At this point, a region-specific multiplier (indemm) can either increase or decrease the initial estimate of INDEM.
A first adjustment to INDEM is related to the world energy price (WEP) and reflects the use of crops for fuel production. Specifically, as the world energy price increases relative to the price in the first year, the industrial demand for crops increases.
[[File:]]
Where
WEP is world energy price
FoodforFuel is the elasticity of industrial use of crops to world energy prices. It starts at a value given by the global parameter elagind, and declines to a value of 0 over 50 years.
The second adjustment relates to the world crop price (WAPf=1); as this increases relative to the price in the first year, industrial demand for crops declines.
[[File:]]
Where
WAP is world crop price
elascd is a global parameter specifying the elasticity of crop demand to global food prices
A third adjustment is based on an assumed cap on per capita industrial demand for crops (IndemCapperPop—hard coded as 2. Specifically, INDEM is not allowed to exceed IndemCapperPop * POP.
For meat and fish, industrial demand is initially calculated by applying the Industrial demand to food ratio, IndToFoodRatI (calculated in the initial year of the model) to the value of food demand.
[[File:]]
Note that there is no multiplier equivalent to indemm for meat and fish.
Finally, as with FDEM and FEDDEM, INDEM may be adjusted to account for excessive consumer spending on food, as described in section 3.2.5 or due to shortages in crops, meat, or fish as described in Section 3.4: Stocks.
3.2.4 Food manufacturing demand
The final demand category, FMDEM, relates to the use of crops, meat, and fish in food manufacturing and processing.
Pre-processor and first year
The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used in food manufacturing and processing.[8] Note that If data are missing, a minimum value of 1 ton, or .000001 MMT is used.
As noted in Box 1, certain adjustments may be made in the pre-processor to ensure consistencies between supply and demand in individual countries, as well as between imports and exports across countries.
Paralleling the case for INDEM, FEDDEM, and AGLOSSTRANS, one other value is calculated in the first year –FManToFoodRatI, which is the ratio between INDEM and FDEM. This is calculated for crops, meat, and fish, and used for all three in the forecast years, as described below.
[[File:]]
Forecast years
In the forecast years, for all three categories, demand is calculated using the Food manufacturing to food demand ratio, FManToFoodRatI, calculated in the first year of the model and the value of food demand.
[[File:]]
As with FDEM, INDEM, and FEDDEM, FMDEM may be adjusted to account for any shortages in crops, meat, or fish as described in Section 3.4: Stocks. It is not currently affected by excessive consumer spending on food, as described in Box 2
'''3.2.5 Total agricultural demand and final adjustment to demand'''
Pre-processor and first year
AGDEM, which represents the sum of all uses. It is initialized in the first year of the model to ensure the balance with production, imports, and exports:
[[File:]]
Forecast years
In the forecast years, AGDEM, is recalculated as the sum of the final values of feed, industry, and food demand and transmission losses:
[[File:]]
Note that this occurs after any adjustments to the demand values as a result of excessive consumer spending on food, (described below), but before adjustments as a result of shortages, describe in Section 3.4: Stocks. Thus, it can be the case that the final value of AGDEM may exceed the sum of the individual demand values.
Final agricultural demand adjustment based on levels of consumer spending
One final adjustment is made to the agricultural demand variables in the forecast years.
If the preliminary estimate of total food demand in monetary terms (csprelim), is too large of a share of consumption, i.e., if
[[File:]]
Where
CSF is the ratio of consumer spending in the agricultural sector in the first year (CSr,s=1,t=1) to DemValr, a weighted sum of demands for agricultural products for food in the first year
[[File:]]
C is total household consumption in the first year
When this is the case, a series of steps are taken to bring these values back in line.
- The necessary reduction (NecReducr), which is in monetary terms, is calculated as CsPrelimr – 0.85*Cr
- A reduction factor (ReducFact) for meat and fish, assuming cuts would disproportionately be there, is calculated as
[[File:]]
with a maximum value of 1 or full elimination
- The physical demands for crops for meat and fish in tons (FDEM, categories 2 and 3) are reduced by reducfact, and the values of the meat and fish reduction are saved for the next step
[[File:]]
[[File:]]
[[File:]] )
- An estimate of the necessary reductions in crops for food, in monetary terms is estimated by subtracting the savings obtained through the reduction in meat demand
[[File:]] * [[File:]] * [[File:]]
- The physical demand for crops for food (FDEM) is then reduced as follows
[[File:]]
Note that this ensures that FDEM is not reduced by more than ninety percent.
Finally, given the changes above, the total demand is recalculated as the sum of the final values of feed, industry, and food demand and transmission losses
[[File:]]
Box 1: Adjustments in the Pre-processor to Ensure Proper Balances The pre-processor reads in data from the FAO Food Balance Sheets and initializes values for the amount of agricultural commodities used for direct human consumption, FDEM, feed (FEDEM), industry (INDEM), food manufacturing (FMDEM), as well as transmission losses (AGLOSSTRANS). All of these are measured in MMT per year. At the same time, it reads in data for production (AGP), imports (AGM), exports (AGX), and total domestic supply (AGDOMSUPP)[1]. A set of conditions should be meet for these variables for each category:
The pre-processor includes procedures to ensure that these three conditions hold for the initial values in each country. This can lead to minor adjustments in the values for the supply and demand categories. These processes can also lead to changes in related variables, including the production of non-animal meat products (CAGPMILKEGGS), fish catch (AGFISHCATCH), aquaculture production (AQUACUL), the size of the livestock herd (LVHERD), and the breakdown of land areas (LD). The latter occurs because we do not want these processes to change crop yields (YL). |
3.3 Trade
Consistent with the approaches within both the economic model and the energy model, trade of agricultural products in IFs uses a pooled approach rather than a bilateral one. That is, we can see the total exports and imports of each country/region, but not the specific volume of trade between any two. Offered exports and demanded imports from each country/region are responsive to the past shares of export and import bases and are summed globally. The average of the totals is taken as the actual level of global trade and the country exports and imports are normalized to that level.
Price differentials across countries do not influence agricultural trade. Although the IFs project has experimented over time with making such trade responsive to prices, there is an increasing tendency globally for food prices to be more closely aligned across countries than was true historically. Moreover, the use within IFs of local relative food surpluses or deficits (as indicated by stock levels) to adjust trade patterns is an effective proxy for the use of prices.
The initial year values of the imports (AGM) and exports (AGX) of the three agricultural commodities in physical quantities are determined in the pre-processor. Since we only have historical data on the imports and exports of fish in monetary terms, these need to be converted to physical terms. This is done by multiplying the monetary values, which are in $billion, by 1000*/2200 to get physical values in million tons. In addition, exports of fish are limited to be less than 70 percent of total fish available and imports less than 1 percent of total fish available. For each of the three agricultural commodity groupings, if there is an imbalance between global imports and global exports in the preprocessor, the latter takes precedence and national imports are adjusted to bring global imports into line with global exports.
In the first year, seven variables are set related to trade for each commodity: XKAVE, MKAVE, XKAVMAX, MKAVMAX at the country level and wxct=1, wmdt=1, and WAPt=1 at the global level.
XKAVE and MKAVE are moving average values of export and import propensity, respectively. They are specified as the ratio of agricultural exports and imports to a base value (xbase) for each commodity. For exports, this is basically the sum of production and demand for that commodity; for imports, it is just demand.
[[File:]]
[[File:]]
XKAVMAX and MKAVMAX are maximum values of XKAVE and MKAVE. For crops and meat, XKAVMAX is set to 1.1 times XKAVE, but is not allowed to exceed a value of 0.7; MKAVMAX is set to 1.5 times XKAVE, but also is not allowed to exceed a value of 0.7. For fish, XKAVMAX is set to 1.1 times XKAVE, with a bound of 0.95; MKAVE is set to 1.5 times MKAVE, with a bound of 2. These values are held constant for all future years.
XPriceTermLag, and MPriceTermLag are set to 0 for all commodities. wxc and wmd are the total world agricultural exports and imports; these are set to a value of 1 in the first year. WAP is the initial world price index for each commodity, which is set to 100.
In the forecast years, the process for determining agricultural imports and exports involves the following steps:
- Estimating the agricultural export capacity and agricultural import demand for each country.
- Reconciling the differences between global agricultural export capacity and global agricultural import demand.
- Computing the actual levels of agricultural exports and agricultural imports for each country
The agricultural export capacity is estimated by multiplying the export propensity (XKAVE) by the current year’s production and demand. It is also limited by XKAVMAX:
[[File:]]
Similarly, the agricultural import demand is estimated by multiplying the import propensity (MKAVE) by the current year’s demand, with a limit set by MKAVMAX
[[File:]]
For each country, values are also estimated for its net surplus or deficit (surpdef) for each commodity. This is based on the following factors: 1) post-loss production, 2) domestic demand, 3) the difference between current and desired stocks, and 4) a trade term
[[File:]]
[[File:]]
[[File:]]
[[File:]]
The first three factors are straightforward. Production minus demand reflects a basic net surplus, which is then adjusted by any net surplus in stocks. The TradeTerm is related the relative role a country plays in global imports and exports and is given as:
[[File:]]
The TradeTerm is positive (negative) when a country has a larger (smaller) share of the global imports than it does of the global exports of a particular commodity and vice versa. Since the TradeTerm is added to surpdef, it acts as a balancing mechanism; countries that appear as relatively larger (smaller) importers get a positive (negative) boost to their estimated net surplus, which tends to reduce (increase) imports as shown below.
At this point, the global sum of exports and imports across countries will likely differ. Therefore, a procedure is required to balance these. In preparation for this one more global variable and several country-level variables are calculated. The global variable is globalsurdefrate, which is the ratio of the sum across countries of net surplus divided by the sum across countries of demand and production, which is the stock base.
[[File:]]
The country-level variables are as follows:
The first term modifies the country’s net surplus, increasing (decreasing) it when the global net surplus is negative (positive).
[[File:]]
The second term modifies how rapidly the net surplus is closed.
[[File:]]
The third term is simply the ratio of exports to the sum of imports and exports.
[[File:]]
The next step is to calculate whether it is necessary to increase (decrease) imports and decrease (increase) exports for each country, and by how much. Whether a country needs to increase its initial estimates of imports and decrease its initial estimates of exports, or vice versa, is determined by the sign of countryextrasurdef. If this value is negative, i.e., the country has a net deficit, it will need to reduce exports and increase imports. The opposite holds for when countryextrasurdef is positive.
As for the amount by which imports and exports need to be increased or decreased, this is a function, in general, of the size of the necessary adjustment and the export share:
[[File:]]
[[File:]]
Note that the sign of countryextrasurdef and the fact that exportshare is a value between 0 and 1 ensure that when exports increases, imports fall, and vice versa.[9] Finally, in this adjustment process, exports and imports are not allowed to fall by more than half or more than double.
This process may not fully reconcile global trade, so a final adjustment is made by setting world trade (WT) as the average of global exports and imports and then adjusting the country values accordingly:
[[File:]]
[[File:]]
[[File:]]
IFs can now update the moving average export (XKAVE) and import (MKAVE) propensities for the next time step. The weights given to history are set by the global parameters xhw and mhw. For small exporters, i.e., where exports are less than one tenth of the sum of production and demand, xhw is reduced by 40 percent, allowing for faster adjustment. XKAVE and MKAVE are updated as
[[File:]]
[[File:]]
For crops, the import propensity is bound from below by a factor given by potential GDP (GDPPOT), demand (AGDEM), the conversion factor between agricultural imports in physical terms and dollar values (msf, see section on links to the economic model), and the initial world price for agriculture (WAP).
[[File:]]
Finally, XKAVE and MKAVE are bound from above by XKAVMAX and MKAVMAX, respectively.
3.4Stocks
First year
Due to a lack of good historical data, in the first year, stocks for all three agricultural commodities are assumed to equal desired stocks. These are set to a fraction (agdstl) of total production (AGP) and demand (AGDEM) for each commodity.
[[File:]]
Where
Agdstl is a parameter used to set desired stock levels for agricultural commodities. It is set to be 1.5 times dstl, which is a global parameter that can be adjusted by the user
Forecast years
In future years, basic stock levels (CumStk) increase with production (AGP), decrease with demand or consumption (AGDEM), and adjust for net imports (AGM-AGX).
[[File:]]
[[File:]] )
Of course, the actual stock values (FSTOCK) are not allowed to go negative. If the basic stock level is negative, stocks are set at zero and a shortage (Sho) exists, which affects calorie availability. If the basic stock level is positive there is no shortage and stocks equal the basic level.
[[File:]]
[[File:]]
Also, if shortages are greater than 0, a reduction factor (ReductionFactor) is computed which is then used to adjust demand and losses.
[[File:]]
[[File:]]
[[File:]]
[[File:]]
[[File:]]
[[File:]]
3.5 Calorie Availability
Daily per capita calorie availability (CLPC) is initialized in the pre-processor. Where available, data is taken from the FAO[10] It is multiplied by population (POP) to yield total daily calorie availability and brought into the model with the name CLAVAL. We already saw that this first year value is used in the calculation of two country-specific factors: 1) calactpredrat, which is a shift factor determined as the ratio of calorie availability to predicted calorie demand in the first year, and 2) sclavf, which is a conversion factor relating the total annual demand for food crops and crop equivalents from meat to daily calorie availability.
In the forecast years, CLAVAL is calculated using the final value of calories per capita.
[[File:]]
Calorie availability combines with regional calorie need in the population model for the calculation of possible starvation deaths (a seldom used variable because in official death statistics people do not die of starvation but rather of diseases associated with undernutrition); the population and health models therefore look instead to the impact of calorie availability on undernutrition and health.
3.6 Prices
IFs keeps track of both national (FPRI) and world (WAP) price indices for each of the three agricultural commodities. All of these are set to an index value of 100 in the building of the base.
The national crop price indices (FPRI, category (1) respond to: 1) changes in global costs of crop production, the latter being expressed as the ratio of global accumulated capital investment in crops to global production and 2) changes in the level of domestic crop stocks. The first factor should provide a long-term basis for rising or falling prices tied to changing technology and other factors of production; the second factor generally should represent shorter-term market variations from that long-term level.
The impact of global costs is given by dividing the ratio of global investment in crops to global production (wkagagpr) in the current year to that same ratio in the first year. The effect of stocks on crop prices (Mul) is calculated using the same ADJSTR function introduced in the description of crop supply, which considers the difference between both the current crop stocks and a desired vale and between current crop stocks and those in the previous year. Two parameters control the degree to which these two ‘differences’ affect the calculation of the adjustment factor. In this case, these are the global, user-controllable parameters fpricr1 and fpricr2. All together the equation for domestic crop price indices in the coming year is given as
[[File:]]
The domestic crop price indices are also bound between 0.01 and 1000.
The national meat price indices are linked the global crop price. Specifically, they are given as a moving average of the global crop price index
[[File:]]
Where
fprihw is a global parameter used to control the speed at which the domestic meat price changes.
The national fish price indices are all set equal to the global fish price index. The determination of the global fish price is similar to that for the national crop price, but here the stock of interest is the global stock and there is no effect related to costs. The ADJSTR function is used once again to calculate the adjustment factor (MUL), this time focusing on the desired global fish stock, the difference between this and the current global fish stock, and the change in the global fish stock in the past year. Again, two parameters control the degree to which these two "differences" affect the calculation of the adjustment factor. In this case, these are the global, user-controllable parameters fprim1 and fprim2. The global and national fish prices are thus calculated as
[[File:]]
The world price indices for crops and meat are computed, in the following year, as a weighted average of the domestic prices, with the weights given by crop and meat production:
[[File:]]
3.6 Returns and Profits
IFs estimates the net returns in agriculture (AGReturn) for each commodity as the ratio of gross returns (GReturn) to production costs (ProdCost and MProdCost). The agricultural profit ratios (FPROFITR) are then estimated as the ratio of AGReturn in the current year to its value in the initial year. At some points in the evolution of IFs we have used FPROFITR as a guide to rates of investment (see the calculation of mulrprof in All but First 2: Investment); the current formulation for investment does not do so. For completeness, however, we provide a description of these processes in the model, as they still exist as live code.
Pre-processor and first year
In the first year, values for FPROFITR, sfprofitr, and FPRofitR are all set to 1.
Forecast years
The production costs for crops are estimated as the cost of cropland, priced at the cost of new land development (CLD), plus the investment in agricultural capital (KAG). The net revenues are given as total yield times the domestic crop price index. This results in
[[File:]]
[[File:]]
For meat, production costs are estimated by the value of the crop equivalents produced by grazing and the cost of feed, where the value is given by the domestic meat price index. The net revenues are based on the size of the herd and the domestic meat price index. This results in
[[File:]]
[[File:]]
For fish, the production costs are simply estimated by the total production of fish times the domestic meat price index. The net revenues are given as the total production of fish times the domestic fish price index. This implies
[[File:]]
[[File:]]
The net returns for each commodity can then be calculated as
[[File:]]
These net returns are used to account for changes in profits over time, using the variable FPROFITR, which influences investment in agriculture. This variable is calculated for each commodity as
[[File:]]
A similar variable (wfprofitr) is calculated at the global level as a production weighted average of country/region values, but only for crops.
[[|3.7 Investment]]
Investment in agriculture is relatively complex in IFs, because changes in investment are the key factor that allows us to clear the agricultural market in the long term. It is very similar to investment in energy, except that we do not need to compute type-specific investments—capital in agriculture is only used for the production function of crops.
We calculate a total agricultural investment need (INAG) to take to the economic model and place into the computation for investment among sectors. This calculation involves multiple factors. These begin with an initial estimate or targeted level of investment (TInAg) that is the product of the ratio of investment to GDP in the previous year times the GDP in the current year.
Three factors modify that basic or target investment level. Two of those are global and one is regional. The first global factor is a multiplier linked to year-to-year change in the ratio of agricultural demand to GDP (WAgDemRMul); typically agricultural demand grows more slowly than GDP. The second is a multiplier responsive to the level of global stocks (MulWSt); if those drop below target levels it would increase production globally and vice versa. The model could use a global price average instead of stocks, but in the recursive structure stocks determine prices and therefore use of stocks accelerates responsiveness of investment. Similarly, the regional factor represents a multiplier tied to regional stock levels (MulSt).
[[File:]]
where
[[File:]]
To elaborate, MulWSt and MulSt are adjustment factors related to global and domestic crop stocks, respectively. Both use the PID ADJSTR function described earlier, just as changes in prices use it in order to set prices that change year-to-year so as to chase supply-demand equilibration over time. For MulWSt, the controlling parameters in the PID function for stocks versus targets and changes in stocks are hard coded with values of -0.3 and -0.9, respectively. For MulSt, these parameters are hard coded with values of -0.2 and -0.4, respectively.
Experience with that initial estimate, however, shows that it can be overly responsive to one or more of the multiplicative adjustment factors, thereby setting up behavior that oscillates. Therefore the next step is to compute a smoothed rate of investment as a share of GDP (SmInAgR). That rate gives more weight (60 percent) to the final investment rate in the previous year than it does to the rate that results from the initial target investment calculation. The overall result of this process is to smooth changes in the rate of investment over time. Desired investment (INAG) is the product of that smoothed rate and GDP.
[[File:]]
where
[[File:]] )
To further prevent too rapid of a shift in demand for agricultural investment, INAG is not allowed to increase by more than 30 percent or decrease by more than 25 percent from the actual investment in the current year. A second check ensures that the demand is no less than 0.5 percent and no greater than 40 percent of current agricultural capital (KAG).
At this point a user-controlled country-specific multiplier aginvm can boost or reduce INAG. One final check ensures that as long as GDP in the country is larger than it was in the first year, the demand for agricultural investment is not allowed to decline at an annual rate of more than 1 percent per year from the first year.
Investment need (INAG) then enters the economic model, which returns a value reconciled with all other investment needs and that feeds into further calculations in the agriculture model.
3.8 Economic Linkages
Several variables, such as gross production, stocks, consumer spending, trade, prices and investment, are common to both the economic model and the two physical models. But hardly ever will the economic and physical models produce identical values, even during the first time step when both utilize "data." Thus, although we want the physical model value to override that of the economic model, it cannot simply replace it. Instead IFs extensively uses a procedure of computing an adjustment coefficient during the first time step. That coefficient is the ratio of the value in the economic model to the value in the physical model. In subsequent years IFs uses that coefficient to adjust the value from the physical model before its introduction into the economic model.
Gross production (ZS) in the agricultural sector illustrates this procedure. The value of gross production in the agricultural model is the sum of the products of agricultural production (AGP) and prices (WAP) in each agricultural category. Multiplying that times an adjustment factor (ZSF) computed in the first time stop to assure inter-model consistency produces gross production for the economic (ZS). World average prices (WAP) are used in all the economic/physical model conversions because they assure that global sums (e.g. of exports and imports) will balance.[11]
[[File:]]
Where
[[File:]]
Similarly, food stocks in each category (FSTOCK) and an adjustment factor (FSF) produce stocks (ST) for the economic model.
[[File:]]
Where
[[File:]]
A similar translation is made for consumer spending on agricultural commodities, recognizing that not all crop demand is directly by consumers.
[[File:]]
Where
[[File:]]
In the same fashion exports (AGX) and imports (AGM) from the agricultural model allow calculation of exports (XS) and imports (MS) for the economic model.
[[File:]]
Where
[[File:]]
and
[[File:]]
where
[[File:]]
A check and, if necessary, adjustment is made ensure that the monetary values of imports and exports match up at the global level.
[[File:]]
and
[[File:]]
With respect to prices, the agriculture model passes to the economic model a value (PRI), which reflects the ratio of the current domestic crop price index to the initial world crop price index.
[[File:]]
Finally, investment need (INAG) is passed to the economic model under the variable name IDS, category 1 (agriculture).
3.9 Capital Dynamics
The economic model of IFs returns a (potentially) modified value of IDS, category 1, reflecting the total amount of capital available for agriculture. This value is assigned to the variable IAval, which overrides the value of INAG calculated earlier (earlier it was basically investment demand; after return from the economic model it becomes investment supply).[12] The agriculture model divides the investment available for agriculture (IAval) into investment for cropland development and investment for other agriculture capital. The coefficient IALK indicates the portion going to cropland development.
IALK is set to a default value of 0.25 for all countries in the pre-processor. In forecast years, IALK changes from this initial value depending on change in the ratio of return on land (RETR) to return on capital (RETK).
IFs calculates the return rate on land as the crop yield (YL) in the first year divided by the current cost of developing a unit of cropland (CLD).
[[File:]]
The return on capital depends on the difference between the hypothetical level of crop yield (HYL) that could be obtained from an additional unit investment in agricultural capital and the crop yield without that increment (CompYl). Recalling how crop yield is estimated, the hypothetical crop yield is given as
[[File:]]
[[File:]]
and the return on capital is given as
[[File:]]
The ratio of the return to land to the return to capital (RETRAT) is given as
[[File:]]
The adjustment of IALK uses the same first and second order adjustment mechanism that we have seen before with the ADJSTR function. Here the ‘target’ level is the ratio of the return to land to the return to capital in the first year.
[[File:]]
Where
eliasp1 and eliasp2 are global parameters
Two final checks are made on the value of IALK. First, it is not allowed to exceed a value related to the cost of replacing depreciated investment in land and bringing a portion of grazing or forested land into production.
[[File:]]
Second, IALK is bound between 0.1 and 0.8.
Finally the model updates agricultural capital (KAG) for the next year by subtracting depreciation as represented by agricultural capital lifetime (lks), adding the residual (non-land) investment, and adjusting for any civilian damage from warfare (CIVDM – see international politics model documentation).
[[File:]]
3.10 Land Dynamics
Land in IFs is divided into five categories—crop, grazing, forest, urban, and other land. Historical data on total land area (LDTot), crop land (LDl=1), grazing land (LDl=2), forest land (LDl=3), and other land (LDl=4) are taken from FAO data. Historical data on urban land (LDl=5) is taken from WRI.
Pre-processor and first year
A few adjustments to the historical data are made in the pre-processor.
- In the pre-processor total production of food is reconciled with the total trade. In cases where, demand is greater than domestic supply of crops, crop production is increased to reconcile demand with supply of food production. Crop land is also increased proportionately.
- If urban land is more than three quarters the area of other land, land is shifted from urban to other land
- If no data is available for crop land, the same is set to 30 percent of total land area. If no data is available for grazing land, same is set to 5 percent of total land area. If no data is available for other land, same is set to 30 percent of total land area.
After these changes, total land area is recomputed as the sum of the area of the individual land categories.
The pre-processor also reads in a value for potentially arable land (landarablepot), which affects the amount of potential cropland in the model. The share of agricultural capital going to land (IALK) is set to 0.25 in the pre-processor.
One final parameter is estimated related to land in the pre-processor. This is the target rate of growth of cropland (tgrld). When data is available, this is currently estimated as the growth rate of cropland between the year 2015 and the year 2005.
[[File:]]
When no data are available for cropland in either 2015 or 2005, the target rate of growth of cropland is estimated as a function of average income
[[File:]]
with a maximum growth rate given as a function of cropland as a share of total land
[[File:]] )
Finally, this target growth rate is restricted to fall between -0.003 and +0.01.
In the first year, IFs estimates an initial unit cost of cropland development (CLD) as
[[File:]]
where
IDS is the total investment in agriculture
IALK is the share of agricultural investment going to cropland development
dkl is a global parameter indicating the depreciation rate of investment in cropland, essentially a maintenance cost for existing cropland
tgrld is the target growth rate for cropland
A related factor (SCLdF), to be used in determining the cost of land development in future years, is also calculated in the first year
[[File:]]
Forecast years
IFs calculates changes in land use for the coming year as a result of four key dynamic processes. First, changes in urban land may result from income and population changes. Second, economic shifts related to investment, particularly in the agricultural sector, can affect the amount of cropland. Third, IFs there can be expansion or retirement of grazing land for undefined reasons. Finally, in certain scenarios, specific changes in forest land can result from policies related to issues such as conservation and environmental protection.
3.10.1 Changes in urban land from income and population changes
Changes in urban land result from changes in population and income. IFs first estimates a predicted level of urban land (LandUrbanPred), which is then compared to current urban land. Any changes are assumed to affect all other land types proportionately, unless this leads to not enough land in a particular category. The growth with income is based on an estimated relationship between income and urban land per capita (LandUrbanR)
The predicted level of urban land (LandUrbanPred) is then given as
[[File:]]
The change in urban land (NUrbLD) is then calculated as
[[File:]]
Limits are placed on the change in urban land area. First, if urban land is growing, the amount of increase in a single year cannot exceed 1/100th of a variable that is related to the change in the non-urban share of all other land from the base year (NonUrbanShrR)
[[File:]]
where
[[File:]]
Second, if urban land is declining, it is not permitted to fall below 10,000 hectares. Third, the changes in Urban land are assumed to affect all other land categories proportionately
[[File:]]
However, this is not allowed to result in the area for a given land category falling below 1,000 hectares. Thus, there may be a slight reduction in the amount of new urban land in certain cases.
3.10.2 Changes in cropland due to investment and/or depreciation.
The changes in cropland are driven by the economics of land. Specifically, they are a function of the profitability of cropland. Also, they are assumed to affect, at least directly, only the forest and the other land categories.
A maximum amount of cropland expansion each year (MaxLandExpansion) is fixed by the amount of forest land, the amount of other lands, the amount of potential arable land, and the existing amount of cropland. The maximum amount of expansion must be at least 2/100th of the existing cropland, but beyond that it cannot exceed either the total amount of forest and other land or the difference between 110% of the potential arable land (landarablepot) and current cropland.
The change in the amount of cropland and the initially estimated share of agricultural investment going to cropland in the following year are computed differently depending upon the maximum amount of cropland expansion relative to the amount of existing cropland and the current level of average income in a country. Specifically, if the maximum amount of cropland expansion is less than 10 percent of existing cropland then it is assumed that there is no change in cropland (lddev = 0) and that no agricultural investment is targeted for cropland development (IALK = 0).
If the condition mentioned in the previous paragraph is met, i.e., there is an ‘adequate’ amount of land for expanding cropland, the amount of change in cropland (lddev) is initially calculated as
[[File:]]
where
IAval is the total amount of funds available for investment in agriculture which is equal to IDS
IALK is the share of agricultural investment going to cropland development
CLD is the unit cost of cropland development
dkl is the depreciation rate of investment in cropland (essential a maintenance cost for existing cropland)
ldcropm is a country-specific multiplier that can be used to increase or decrease changes in cropland
Note that this equation takes into account the need to maintain existing cropland. Also, at this point, the value of LdDev is bound from below to ensure that it does not imply a greater than 10 percent decrease in existing cropland. For relatively poor countries (GDPPCP < 10), the constraint is even stricter. Specifically, IFs calls for a shift in funds to ensure that no cropland is lost. The desired shift in funds is given as
[[File:]]
The actual shift in funds is limited to 90 percent of the available funds, however, where the available funds are the investment in agriculture not initially designated for cropland development
[[File:]]
The value of lddev given the actual shift in funds is given as
[[File:]]
In addition, the share of investment in agriculture designated for cropland development is updated to be[13]
[[File:]]
The changes in cropland are linked to changes in land in the forest and ‘other’ categories. The amount coming from/going to forests reflects the share of forest land relative to ‘other’ land, as well as the current level of development. For countries with a GDP per capita higher than 15,000 dollars and where LdDev is less than 0, more is given back to forest land and the ForShrPar is set to 0.25.
[[File:]]
where
[[File:]]
ForShrPar is given by the function depicted below
The solid line holds when land is being converted from forests to cropland (lddev > 0) and the dotted line holds when land is being converted from cropland to forests (LdDev < 0). In either case, this implies that the less of the change is related to forest land than would be expected by its share.
Two other qualifiers are that the changes in forest land (LDDEVFor) and the changes in ‘other’ land cannot exceed 90 percent of existing land in these categories and the shifts cannot result in either land category falling below 1,000 hectares. These limits feedback to the change in cropland, finally resulting in the following
[[File:]]
[[File:]]
[[File:]]
[[File:]]
Turning back to the future cost of cropland development, this is estimated differently based only on whether there is ‘adequate’ room for cropland land expansion, defined as when the maximum amount of cropland expansion is greater than 10 percent of existing cropland. If this is the case, the future price of cropland is estimated as
[[File:]]
where
RemRat is the ratio of the maximum land for expansion in the first year to the maximum land for expansion in the current year, with a maximum value of 10
[[File:]]
This basically states that the price of cropland development grows linearly with growth in cropland and exponentially with declines in available land for cropland expansion.
Alternatively, if the maximum amount of cropland expansion in a given year is less than or equal to10 percent of existing cropland, the cost of bringing new land under cultivation is assumed to grow at the maximum of either 2 percent per year from the cost in the first year or the growth of cropland from the first year. Furthermore, it is not allowed to decline. Thus
[[File:]]
3.10.3 Changes in grazing land
IFs assumes that relatively poor countries (GDPPCP < 10) will continue to develop additional grazing land, whereas relatively rich countries (GDPPCP > 15) will retire grazing land. No change is expected in countries with average income between $10,000 and $15,000. The annual expansion of grazing land in poor countries is initially estimated as 0.5 percent of the amount of grazing land in the first year. The retirement of grazing land in richer countries is initially estimated as 0.2 percent of current grazing land.
As with cropland, any changes in grazing land will be compensated by changes in forest and ‘other’ land. Each category is initially assumed to be affected proportionately, e.g.,
[[File:]]
Unlike the case for changes in cropland, there is no adjustment to the forest share as a function of income or the direction of change in grazing land. As with the changes in cropland, however, the changes in forest and ‘other’ land cannot exceed 90 percent of existing land in these categories and the shifts cannot result in either land category falling below 1,000 hectares. Again, these limits feed back to the change in grazing land.
3.10.4 Change in forest land due to a policy choice
The model user can also force the land in forest area to increase or decrease at the expense of crop and grazing land via a forest multiplier forestm. The change in forestland, LDSHIFT, is bound. In the case of an increase, i.e., forestm > 1, the amount of added land is limited to 20 percent of crop and grazing land; in the case of a decrease, i.e., forestm < 1, the amount of forest land removed is limited to 20 percent of existing forest land.
[[File:]]
[[File:]]
The amount of land taken from cropland and grazing land is proportional to the amount of each.
[[File:]]
[[File:]]
[[File:]]
3.10.5 Final checks and renormalization of land use
Two final adjustments are made to the land area values to clean up any quirks that might have be introduced in the previous processes. First, the values for each category are bound between one thousand and ten billion hectares. Second, the values are normalized so that the sum of the categories equals the total amount of land.
[[File:]]
Finally, a value for world forest area (WFORST) is calculated at the end of this process by summing forestland area across all countries.
[[File:]]
3.11 Livestock Dynamics
In addition to capital and land, the other "stock" or "level" variable with important temporal dynamics is the livestock herd (LVHERD).
Pre-processor and first year
In the pre-processor, as explained earlier, the values for total meat production and animal meat production are initialized. From these values, IFs calculates the value for livestock by dividing the total animal meat by the slaughter rate (slr)
Forecast years
The value of LVHERD is calculated by using pre-production loss meat production (AGPppl), adjusting the same for animal products produced (AGPMILKEGGS). This gives total animal meat production. The animal meat production is then divided by the slaughter rate slr[14].
[[File:]]
3.12 Water Dynamics
Water use begins with data on total water withdrawals from FAO Aquastat. These are divided by the size of the population to get an estimate of water use per capita.
In future years, water use per capita is forecast to increase in parallel with crop production per capita. Specifically, an expected level of water use per capita as a function of crop production per capita (see figure below) is calculated for crop production in the current year (CropPC) and crop production in the first year (CropPCI). The ratio of these values is multiplied by the water use per capita in the first year (WatUsePCI) to get water use per capita in the current year (WatUsePC). This is multiplied by population (POP) to get total water use (WATUSE)
[[File:]]
[[File:]]
[[File:]]
Figure 19: Relationship between water use per capita and Crops production |
[[File:]]