Model validation and verification

Introduction^[1]

The purpose of a model is to answer questions. In the case of the International Futures (IFs) model, the purpose is to answer “What if?” questions. For example, “What if the system begins in a certain state and behaves according to a series of assumptions?” and “What if this initial state and/or the assumptions were to change?” Exploring and understanding these questions will ideally lead to better informed decisions. The user of IFs, basing decisions off the outputs of the model, will naturally question whether the outputs are “correct.” Model verification and validation are the processes through which we can address these concerns.

 

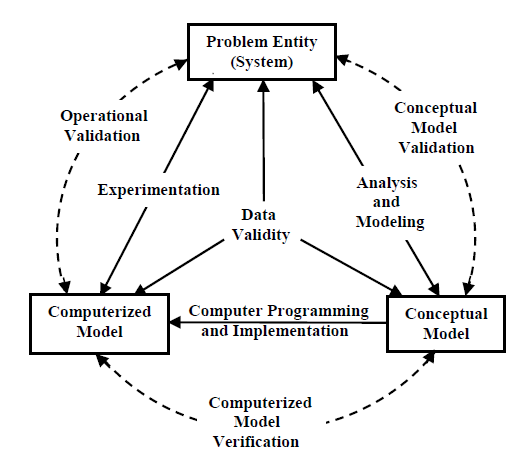
Model verification and validation are crucial in the model development process. Below is a graphic illustrating the role of verification and validation in this process. The “problem entity” is the system being modeled. The “conceptual model” is the formal, logical representation of the system being modeled (problem entity). The “computerized model” is the conceptual model implemented on a computer. The conceptual model is developed through a “analysis and modeling” phase, the computerized model is developed through a “computer programming and implementation phase” and inferences about the problem entity can be drawn though the computerized model through an “experimentation” phase.

 

(Sargent, n.d.) defines the different types of validation and verification as follows:

 

“Conceptual model validation is defined as determining that the theories and assumptions

underlying the conceptual model are correct and that the model representation of the problem entity is “reasonable” for the intended purpose of the model.”

 

“Computerized model verification is defined as assuring that the computer programming and implementation of the conceptual model is correct.”

 

“Operational validation is defined as determining that the model’s output behavior has sufficient accuracy for the model’s intended purpose over the domain of the model’s intended applicability.”

 

“Data validity is defined as ensuring that the data necessary for model building, model evaluation and testing, and conducting the model experiments to solve the problem are adequate and correct.”

Validation techniques

(Sargent, n.d.) outlines various validation techniques, and we use the following to validate IFs:

 

“Face Validity: Individuals knowledgeable about the system are asked whether the model and/or its

behavior are reasonable. For example, is the logic in the conceptual model correct and are the model’s input-output relationships reasonable?”

 

Traces: The behaviors of different types of specific entities in the model are traced (followed)

through the model to determine if the model’s logic is correct and if the necessary accuracy is obtained.

 

Comparison to Other Models: Various results (e.g., outputs) of the simulation model being validated

are compared to results of other (valid) models. For example, (1) simple cases of a simulation model are

compared to known results of analytic models, and (2) the simulation model is compared to other simulation models that have been validated.

 

Degenerate Tests: The degeneracy of the model’s behavior is tested by appropriate selection of values

of the input and internal parameters. For example, does the average number in the queue of a single

server continue to increase over time when the arrival rate is larger than the service rate?

 

Extreme Condition Tests: The model structure and outputs should be plausible for any extreme and

unlikely combination of levels of factors in the system. For example, if in-process inventories are zero,

production output should usually be zero.

 

Parameter Variability - Sensitivity Analysis: This technique consists of changing the values of the input

and internal parameters of a model to determine the effect upon the model’s behavior or output. The

same relationships should occur in the model as in the real system. This technique can be used qualitatively—directions only of outputs—and quantitatively—both directions and (precise) magnitudes of outputs. Those parameters that are sensitive, i.e., cause significant changes in the model’s behavior or output, should be made sufficiently accurate prior to using the model. (This may require iterations in model development.)

 

Internal Validity: Several replications (runs) of a stochastic model are made to determine the amount

of (internal) stochastic variability in the model. A large amount of variability (lack of consistency) may

cause the model’s results to be questionable and if typical of the problem entity, may question the appropriateness of the policy or system being investigated.

 

Historical Data Validation: If historical data exist (e.g., data collected on a system specifically for

building and testing a model), part of the data is used to build the model and the remaining data are used

to determine (test) whether the model behaves as the system does. (This testing is conducted by driving

the simulation model with either samples from distributions or traces (Balci and Sargent 1984b).)

---

[1] The methodology behind these verification and validation techniques comes from (Sargent, n.d.).