Labor

Workers in an economy supply the expertise and the efforts needed to produce goods and services. In return the labor receives wages that they use to meet their current and future consumption needs. On one hand, shortage of labor with required skills prevents economies from realizing their growth potential. On the other hand, individuals falling short of the right qualifications might remain unemployed or underemployed failing to secure income needed for a decent living. The ongoing adjustments to find the best match between skills, jobs and wages can only be studied through a dynamic model of the labor market.   

Such a model should go beyond providing a reasonable answer to the obvious question of why employment and wages go up and down. An aggregate labor market must deal with issues that have strong interconnections with various other dynamic changes in the greater society. What kind of dividend of deficit can a society expect from its labor force given the phase of demographic transition in which it is situated? How severely would aging affect the pool of working age adults? Might increasing female participation rates offset some of the losses from aging? What is the level of skills and educational attainment in a society? These supply phenomena move relatively slowly unless there are huge disruptions, like a war or famine, or an aggressive policy push. The demand side, in contrast, needs to be more responsive in adjusting wages and employment given the investment and technology in the various sectors of the broader economy. In general, though, the labor market demonstrates some sluggishness compared to the goods and services markets as it involves moving human beings with various limitations. Consumption of goods and services depend on the income earned by the labor. Uneven distribution of employment and wages among labors of various types or between labor and capital for a long period of time can give rise to persistent inequality in a society.     

Conceptual Framework

Labor markets are markets for workers and jobs. In a labor market, employers meet their demand for labor with the supply of people willing to work at the wage the employers can offer. The employers raise the wage when there is a shortage of workers. Workers agree to take a lower wage when there are more of them than the firms need. In the real-world labor markets do not always clear at perfect equilibrium. Frinctional unemployment results for various reasons, for example, the search time between jobs. Structural unemployment can result from technology induced disruptions. Some unemployment could thus persist in the labor market even when there aren’t any short-term fluctuations. There is also the phenomenon of informal employment that consists of less sophisticated workers and entrepreneurs engaged in unregulated economic activities.  In a dynamic model that covers the entire economy, the real wage earned by the labor drives the income and social mobility.   

To understand the long-term dynamics of the labor market, we need also examine the deeper determinants of labor demand and supply, the determinants that can shift the curves. Labor demand changes over time with the changes in demand for goods and services and the labor input needed to produce those. Labor productivity itself improves with technological progress. Long term transitions in the supply of labor are mostly demographic.  

Labor supply is determined by the working age population and the share of that population who are available for participation in the workforce. The labor supply is relatively stable as the demographic changes are slow in pace. As the share of elderly in the population increases, a recent trend in many societies, the rate of participation declines. Some of the aging impacts will be offset by the greater female participation rates, a second trend that surfaces as economies develop and women attain more education. Educational attainment also drives the general skill level of workers, male and female. Specific skills are obtained through training and experience that augment the knowledge obtained through general and specialized education.     

It is the demand side that causes most of the short-term imbalances in the labor market.  In the long term, as said earlier, the important driver of demand for labor and their skills is technological progress. Labor requirement drops with advances in technology, more so for less skilled labor. Labor composition changes accordingly both within and across sectors. Rapid advances in technology can also cause disruption in the system when there is not much opening in the other sectors. Labor displacement is offset to some extent by the growth in the economy and the resulting increase in total demand.    

As we have already mentioned, employees maximize income and the firms minimize labor costs. When there are more laborers than the firms can hire, there is unemployment. Shifts in the rates of unemployment impacts wage, the price of labor. For example, wages drop in the event of rising unemployment as there are more people to hire from. Wage adjustments feed back to the demand for labor seeking to bring the market back to equilibrium.

The challenges around the conceptual distinction between unemployment and employment is further complicated by the phenomenon of informal employment. In many developing countries there is a large urban non-agricultural informal sector where low-skilled workers work for wages typically lower than a formal employment.

Description of the labor model

Dominant Relations

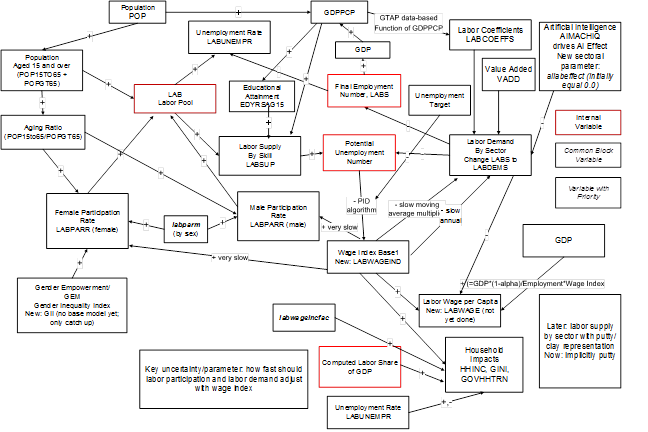
The labor model in the International Futures system (IFs) balances the total supply of labor with the total labor demanded by all economic sectors. Total labor (LAB) is computed from the working age population and the labor participation rate. Population forecasts are obtained from the IFs demographic model. Participation rates (LABPARR) are computed by sex with a catchup algorithm for the female participation towards that for the male. Labor is also disaggregated by skill level, as determined by educational attainment, in a separate labor supply variable (LABSUP) which is used to distribute labor earnings by skill level. [** LABSUP do not affect the demand/supply balance now]

Labor demands (LABDEMS) are driven by sectoral technology functions used to compute the labor requirement by skill level for each unit of potential valued added in the sector. These labor coefficients (LABCOEFFS) are multiplied with the projected value added for the sector to compute the needed manpower. The balancing mechanisms determines the labor employed in each of the sectors (LABS).  

The balancing, in the current version of the model, can be done in one of the two ways. In the first method, total needs combined from all economic sectors is normalized to the available pool of labor computed by subtracting the unemployed from those who are at or looking for work. The rate of unemployment is kept at its natural rate for which we use the base year rate of unemployment. (** This might need to be changed for countries where the market is undergoing some abrupt transition.)

In the second balancing method, added in a recent revision of the model, total demand is equilibrated to supply through a CGE like market equilibrium model. An indexed wage (LABWAGEIND) and the rate of unemployment (LABUNEMPR) work as the equilibrating variables. As unemployment deviates from the target, PID algorithms send a signal for the wage to adjust. Wage adjustments cause adjustments in the “base” labor demands by sector computed from the labor-coefficient functions as described earlier. Wage signals also affects the labor participation rate. The magnitude of impact on the supply side is much lower than that on the demand side.

Wage and unemployment rate are aggregated for the total labor market. The wage index starts with a base year value of 1 and the unemployment rates start with the historical data for the base year. Initial year unemployment rate works as the target for long term unemployment.

Key Dynamics

The following key dynamics are directly related to the dominant relations:

• Labor supply is determined from population of appropriate age in the population model (see its dominant relations and dynamics) and endogenous labor force participation rates, influenced exogenously by the growth of female participation.
• Labor demand is driven by sectoral demand functions driven by technological progress

Structure and Agent System

System/Subsystem	Labor market
Organizing Structure	Labor supply by skill level and labor demand by sector for each skill category represented within an equilibrium-seeking model with wage and unemployment rate as the equilibrating variables
Stocks	Population, labor, education,  accumulated technology
Flows	Participation rate; Coefficients of labor demand; Employment (unemployment); Wage
'Key Aggregate 'Relationships  (illustrative, not comprehensive)	Labor supply is driven by demographic changes; Participation of female change over time; Labor requirement changes with technological development; Unemployment rate drives wage; Wage movements affect labor demand and participation rate
'Key Agent-Class Behavior 'Relationships (illustrative, not comprehensive)	Households and work/leisure, and female participation patterns;   Firms and hiring;

Labor Model Data

The labor supply and unemployment data that we use in our model is from International Labor Organization (ILO). For data on the demand side, we used data from the Global Trade Analysis Project. Wage variable used in the equilibration algorithm is an index anchored to the base year of the model. IFs preprocessor prepared these data for model use using various estimation, conversion and reconciliation processes.     

Definitional Issues

There are ambiguities in the way some of the labor market variables are defined. Labor participation rates and the rate of unemployment are two that need special attention.

The size of the labor supply available for economic activities is expressed with the labor force participation rate. ILO defines this as a “measure of the proportion of country’s working-age population that engages actively in the labor market, either by working or looking for work.” National labor force surveys and census data are used to estimate this rate. The definition of labor force here includes both employed and unemployed and the rate is expressed as a percentage of working-age population. Working-age population is defined here as the population above legal working-age. For international comparability, ILO adopts a convenient minimum threshold of fifteen years as working age and avoids putting any upper age limit. In practice, both the minimum and the upper-age limits can vary by country. For example, the working-age in the USA is sixteen years. In the Netherlands the upper age limit is seventy-five years, whereas South African data uses an upper age limit of 64.

Ambiguities are more abundant in the definition of unemployment. ILO came up with a guideline on this as well. Per the ILO guideline, the unemployed are those among the working-age population who are not employed, are available for work and are actively looking for jobs; the unemployment rate is expressed as a percentage of those who are in the labor force. The availability and job-seeker status could be defined in different ways giving rise to incompatibility in data.  While there seems to be little room for disagreement on whether someone is at work or not, whether that work should be considered as employment is contested at many times.

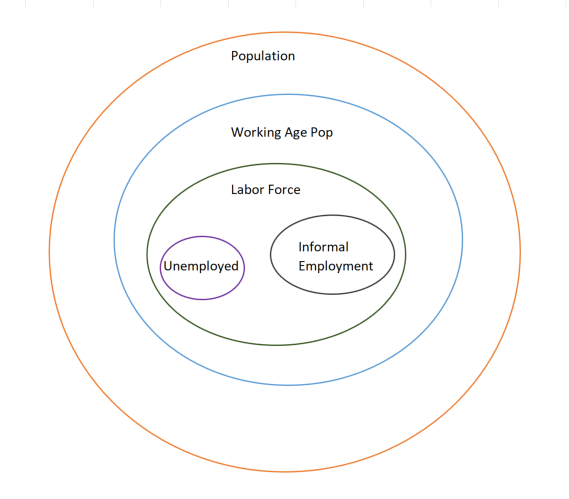
The debates around the nature and type of employment can range from gainfulness to workplace setting. For example, a large number of workers in the low-income low-regulation developing countries work outside the purview of formal enterprises. According to an ILO estimate, more than half of the global labor force and more than 90% of Micro and Small Enterprises (MSEs) worldwide are in the so called informal economy. This might explain the apparently counterintuitive pattern of low unemployment rate in some low-income countries (e.g., 2.2% for Guatemala) and relatively higher numbers for some of the developed nations. The low numbers in the poorer countries hide the prevalence of extremely low wage jobs in the informal sectors in these countries, the only options for the vulnerable people in the absence of any kind of social safety net.  Contrastingly, in the developed countries the so called ‘gig-economy’ is attracting more and more workers who choose to work on their own rather than in a formal enterprise. ILO conceptualization makes the informal work part of total employment. The stacked Venn diagram below presents the relationship among the labor force metric including informal employment. IFs also models informal economy both in terms of GDP share and employment share of informal in the total economy and employment.

Relationship among various labor measurement

Incompatibility can arise in the treatment of various population groups for the computation of the denominator for participation and unemployment rates. ILO makes their best efforts to make adjustments in the data for the sake of international comparison. For example, ILO asks countries that deviate from ILO guidelines to collect data needed to convert national figures to ILO figures. It is likely that some differences might have slipped past the adjustment process. We use ILO data and continue to update our database  

The GTAP data that we use for the demand side of the labor model is taken as labor headcounts and is thus immune from ambiguities around rate computation. As far as we could gather, the data includes both the formal and informal employment. We also need mention here that the GTAP database reconciles the labor data to calibrate the general equilibrium modeling that they do for the trade analyses. The data could thus be somewhat different from data collected through direct surveys. As a CGE model IFs is benefited by using calibrated data.

Sources of Labor Data

IFs model uses ILO data for labor participation rates and for the unemployment rate. The data in IFs are collected from World Bank’s World Development Indicators (WDI) database. According to their documentation, WDI obtained the data from the ILO.

Unemployment rate data in IFs is also collected from WDI. Like the participation rates WDI also obtains their unemployment data from ILO.

For employment and labor demand data IFs uses Purdue University’s Global Trade Analysis Project (GTAP) database. GTAP collects and compiles factor payments, imports, and intersectoral flow data to calibrate CGE models of national economies for trade and other analyses. In their ninth release in 2016, GTAP published data for 140 countries and regions for the year 2011. The earlier GTAP releases, which the IFs model used for its previous versions, compiled data for the years 2004 and 2007. GTAP data release aggregates economic activities into 57 commodities and activities following International Standard Industrial Classification (ISIC). The IFs model maps the 57 GTAP sectors into six economic sectors of IFs – agriculture, energy, material and mining, manufacture, services and ICT. Appendix 2 presents two tables listing the sectors mapping between IFs and GTAP, and GTAP and ISIC. GTAP further disaggregates labor in each of the commodities/activities into five occupation and skill categories following the nine category International Standard Classification of Occupations (ISCO-88). The IFs model collapses five GTAP occupation categories into the simple IFs dichotomy of skilled and unskilled. The mapping of occupations and skills are presented in the third appendix of this document.  

The data in the main GTAP database, prepared for CGE modeling, are all in dollar unit and thus do not include labor headcounts. We have used a ‘satellite’ GTAP database for labor headcounts by skill and sector. The labor counts were also used to plot labor requirement functions for each of the IFs economic sectors and skill categories. The wage share of skilled and unskilled labor in each sector was computed using the labor headcounts and labor payments.

Scope of IFs Labor Model

The IFs labor model simulates labor market at the national level. Each national labor market forecasts labor demand and employment by six sectors - agriculture, energy, mining, manufacture, services and ICT- and two skill levels - skilled and unskilled. The supply side do not have sectoral representation. IFs forecasts total labor force and labor supply by the two skill levels. Labor participation rate is computed in IFs by gender. Wage and unemployment rate is forecast for the overall labor market only.  

Labor Model Pre-processor

IFs system has a data preprocessor that prepares the initial conditions for the model using historical databases and various assumptions and estimated relationships to fill in the missing data and make data adjustments as needed[1]. Pre-processing of labor data takes place in two IFs pre-processing modules. Labor participation rate data, which is closely related to demography, is processed in the population pre-processor. Unemployment rate and labor demand data are processed in the economic pre-processor.  

---

[1] For more details, please see ‘The Data Pre-Processor of International Futures (IFs)” by Barry B. Hughes (with Mohammod Irfan) at http://www.ifs.du.edu/assets/documents/preprocessorv1_0.pdf

Pre-processing Labor participation rate and unemployment

For initializing labor participation rates by sex (LABPARR) the model uses the historical values from the base year or the most recent year with data[1]. For countries with no data we use regression relationships of the participation rates, for men and for women, with income per capita. The relationships, shown in the next figure, are not great. However, the functions affect only five countries for which we do not have any data at all: Grenada, Kosovo, Micronesia, Seychelles and South Sudan[2].

 

---

[1] The data tables that the IFs model pre-processor use for initializing labor participation rates are: SeriesLaborParRate15PlusFemale%, SeriesLaborParRate15PlusMale%.

[2] We should try to collect participation rate for these countries from country sources.

IFs data series SeriesLaborUnemploy% is used for the initialization of unemployment rates. That series has annual unemployment rates for one or more years between 1980 and 2016, for 181 of the 186 IFs countries. For five countries (Grenada, Kosovo, Micronesia, Taiwan and South Sudan[1]) there is no data at all. To fill in the missing data we use a regression function of unemployment rate against GDP per capita. Like the participation rate functions, this function does also not have much of an explanatory power.

---

[1] These are pretty much the same countries for which we do not have any participation rate data. This indicates ILO might have some administrative limitation in reporting data for these countries (notice Kosovo, Seychelles etc in the list)

Pre-processing labor demand and unemployment from GTAP

The IFs economic pre-processor reads labor headcount and labor payment data from the GTAP database. In addition to performing sector and occupation/skill mapping between GTAP and IFs, pre-processor also use the labor headcount data to compute labor coefficient functions, the principal driver of labor demand in the IFs model.

Labor coefficients are defined as the amount of labor needed to produce one unit of value added in a certain sector of the economy. The coefficients depend on the level of technology. The model uses GDP per capita as an indicator of the level of technological development. IFs pre-processor estimates labor coefficient functions for labor of different skill levels for the different sectors of the economy.

The functions are derived from GTAP data we described earlier. The model pre-processor reads data on factor payments and aggregates data from 57 GTAP sectors to six IFs sectors. Shares of payment going to skilled and less-skilled workers in each of the sectors are then computed. Countries are grouped according to their level of technological development as represented by per capita income. For each group labor coefficients are obtained by taking an average of the country coefficients.  We also convert labor payments data to labor headcount data using per capita income as a proxy for average wage. Labor coefficients and income are then plotted into a power function relationship. The figure below plots some of those labor functions.  The functions fit quite well with a power law formulation[1].

---

[1] This is interesting given the prevalence of power law in all sorts of scale-up activities (West 2017).

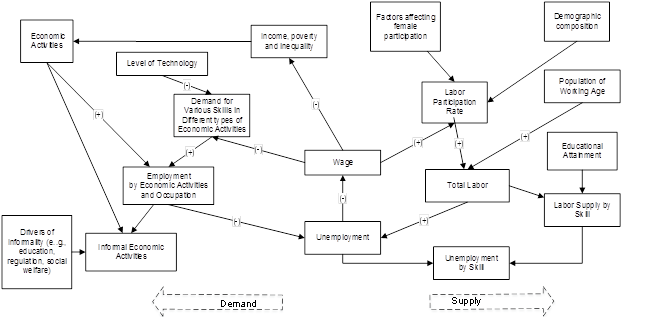
Labor Model Flowcharts

The diagram below shows an outline of the IFs labor model. On the supply side, the total labor pool (LAB) is computed from the labor force participation rates, by sex, (LABPARR) and the population (POP) in their working age, i.e., population over 15 (POP15TO65 + POPGT65). Participation rates are driven by the demographic changes with an additional negative impact from aging and a catch-up in female participation rate. Skill level of the labor supply (LABSUP) is driven by the level of development (GDPPCP) and the demand for labor is driven by labor-coefficients (LABCOEFFS) computed from coefficient function representing shifts in demand with technological progress as proxied by the level of development (GDPPCP). Coefficients computed by sector and skill gives the labor requirement by skill type for each unit of value added (VADD) in the sector. Multiplying these coefficients with projected value added in each sector gives an estimate of the labor demand.  

Any surplus or shortage between total labor demand and supply is used to compute the rate of unemployment. Deviations in the unemployment rate (LABUNEMPR) signal wage changes through an equilibrium seeking algorithm. Both demand and supply respond to the wage variable (LABWAGEIND) indexed to the base year. The supply responses are much slower than the demand responses.

Labor Model Flowchart

Labor Model Equations

Overview

The labor model is a part of the IFs economic model that uses labor model output as an input to a Cobb-Douglas production function in a multi-sector general equilibrium model. IFs is a very long-run dynamic model. Instead of computing fixed short-run equilibria that clear the relevant markets IFs uses an equilibrium seeking algorithm to balance the various systems over the longer run. The algorithm is known as the PID (proportion-integral-derivative) controller algorithm and is used widely in industrial control systems. It makes equilibrium seeking variables in IFs move towards a set target. The algorithm works by computing a multiplier based on the movement of the variable towards the target, as obtained by an integral (I) of the path traversed, and the rate of movement towards the target, the derivative term. The multiplier is applied on the process variable (the P term), or a response variable, in the subsequent time period. In the labor model, unemployment rate (LABUNEMPR) is used as the process variable and the PID multiplier is used on the wage rate (LABWAGEIND). Job availability (LABDEMS) and participation rate (LABPARR) get affected by changes in wage.   

Throughout this section we use subscripts and notations common to other modules of IFs. For example, we use t for time period. Subscripts p and r represent sex and country/region, respectively, c is the cohort number, with cohort 1 representing the newborns, cohort1 the the one-year to four-year-olds, cohort two five-year to nine-year-olds etc. Values for p are 1 for male, 2 for female and 3 for both sexes combined. For economic sectors we use s and for skill levels sk.

Labor Supply: Equations

The total pool of labor is computed by multiplying the population of working age with the labor force participation rate (LABPARR).  Population forecasts come from IFs demographic model which computes both five-year and single-year age-sex cohorts (agedst, fagedst).  

The labor model forecasts participation rates by country/region  and gender. Participation rates in the model move with the changes in the demographic composition. Female participation rates, which have historically been lower than the same for the male in all societies, but has moved up in modern and affluent societies, get a catch-up boost in the model. Participation rates can also change when there is labor shortage or surplus and the employers try to incentivize or discourage workers by changing wage. This last impact is much less slow than similar wage impacts on the demand side.

Labor Participation Rate

Labor participation rates (LABPARR) for male and female are first initialized with historical data.

$LABPARR_{r,p}=LABPARR_{r,p,t=1}$

A ‘catch-up’ boost is added to the female participation rate. The boost added (FemParLabMul) starts at a third of a percentage point and withers away following a non-linear path as the female rates approaches the catch-up target (FemParTar), The maximum catch-up that can occur over the horizon of the model is thirty percent.

$FemParTar_{r}=Amin(LabParRI_{r,p=1},LabParRI_{r,p=2}+30)$

$FemParLabMul_{r}=(FemParTar_{r}-LABPARR_{r,p=2,t-1})/(FemParTar_{r}-LABPARR_{r,p=2,t-1})$

$LABPARR_{r,p=2,t}=LABPARR_{r,p=2,t-1}+FemParLabMul_{r}*0.3$

Next, we compute and apply the aging impact on the participation rate. As the relative share of people over the retirement age increases, the participation rate declines. The model keeps track of the changes in the demographic ratio (PopAgingRatio) of the population who are in their prime working age of 15 to 64 (POPWORKING) to those at a common retirement age of sixty-five or older (POPGT65). This ratio declines as countries age. The percentage drop in the ratio comparative to the base year is scaled appropriately to compute the aging impact (aging_impact). This impact is added to the male and female labor participation rates, with the impact on the female participation rate being slightly lower than that on male rates.

$POPAgingRatio_{r,t}=POPWORKING_{r,t}/POPGT65_{r,t}$

$aging_{i}mpact_{r,t}=100*((POPAgingRatio_{r,t}/POPAgingRatio_{r,t=1})-1)*0.2$

$LABPARR_{r,p=1,t}=LABPARR_{r,p=1,t}+aging_{i}mpact_{r,t}$

$LABPARR_{r,p=2,t}=LABPARR_{r,p=1,t}+aging_{i}mpact_{r,t}*0.95$

Participation rates respond slowly to changes in wage and unemployment rate. The impact is implemented through a wage impact factor computed from annual changes in the wage index (labwageimpact). The base participation rates can be changed by model user through two model parameters: a direct multiplier on the participation rate (labparm), or one that changes participation by moving the retirement age (labretagem)

$LABPARR_{r,p,t}=LABPARR_{r,p,t}*(1-labwageimpact*0.05)*labparm_{r,p,t}*labretagem_{r,p,t}$

Total participation rate (LABPARRr,p=3,t) is computed by an weighted average of male and female participation rates.

$LABPARR_{r,p=3,t}=(sum_{p=1to2}sum_{c=4to21}(agedst{r,c,p,t}*LABPARR_{r,p,t}))/(sum_{p=1to2}sum_{c=4to21}agedst{r,c,p,t})$

Total Labor

Finally, the total number of labor available for work (LAB) is computed by multiplying the total participation rate with the population of fifteen-year-olds or older.

$LAB_{r,t}=LABPARR_{r,p=3,t}*sum_{p=1to2,c=4to21}agedst_{r,c,p,t}$

Labor by skill level

The labor model forecasts labor supply (LABSUP) by two skill categories. The variable (LABSUP) is initialized in the pre-processor by reading the employment by skill/occupation (LABEMPS) data from GTAP[1]  and adding the unemployment numbers. We assume same unemployment rate (LABUMEMPR) for skilled and unskilled labor.

$LABSUP_{r,t=1,sk}=sum_{s=1to6}(LABEMPS_{r,s,t=1}/(1-(LABUNEMPR_{r,t=1}/100))$

The model forecasts labor by skill through a model of the skilled share of the labor. Education, training, exposure, and experience of the employees all improve with the level of development. The model captures this with an analytic function of the skilled share (perskilled) driven by GDP per capita at PPP (GDPPCP) -

$perskilled_{r}=f(GDPPCP_{r})$

Among the causal drivers of skill, education is considered to be the most proximate. Education is strongly correlated with the level of development, the deeper driver of skill in the model. However, the recent increase in education and/or a policy driven educational expansion might add to the impact of education on skill. Additional impacts from education on skill, when there is any, is computed through an expected function formulation. For example, in a society where an average adult has more (or less) education than the adults in other societies at that level of development, the skill share is given a slight upward push (or downward pull). The expectation function is a logarithmic function of educational attainment of working age population (EDYRSAG15) driven by GDP per capita at PPP. Attainment above (or below) the expected level (YearsEdExp) is computed by the function output (YearsEd) adjusted for country situation (yearseddiff). The percentage adjustment to the skilled share (LabSupSkiAdj) is computed using additional (limited) education, i.e., the difference between actual (EDYRSAG15) and expected values of educational attainment, expressed as a percentage of the expected value. The adjustment is scaled appropriately and peters off over time.

$YearsEd_{r,t}=f(GDPPCP_{r,t})$

$yearsdeddiff_{r}=EDYRSAG15_{r,p=3,t=2}-YearsEd_{r,t=2}$

$YearsEdExp_{r,t}=YearsEd_{r,t}+yearsdeddiff_{r}$

$LabSupSkiAdj_{r,t}=0.3*(EDYRSAG15_{r,p=3,t=2}*YearsEdExp_{r,t})/YearsEd_{r,t}$

$LabSupSkiAdj_{r,t}=ConvergeOverTime(0,LabSupSkiAdj_{r,t},70)$

$perskilled_{r,t}=perskilled_{r,t}*(1+LabSupSkiAdj_{r,t})$

The skilled share (perskilled) is multiplied with the total labor supply (LAB) to obtain the number of labors who are skilled (LABSUPskilled)

$LABSUP_{r,skilled,t}=LAB_{r,p,t}*perskilledI_{r,t}$

As a last step, the model adjusts for the country specific variations in the skilled labor count not captured by the deeper and the proximate models. This is done by saving a ratio (LABSUPSkilledRI) of the actual historical data and the model computed value in the initial year. In the subsequent years this ratio is used to adjust the skilled labor forecast gradually.

$LABSUPCompSkilled_{r}=LAB_{r}*perskilled_{r,t=1}/100$

$LABSUPSkilledRI_{r}=LABSUP_{r,skilled,t=1}/LABSUPCompSkilled_{r}$

$LABSUP_{r,skilled,t}=LABSUP_{r,skilled,t}*ConvergeOverTime(LABSUPSkilledRI_{r},1,85)$

Number of unskilled labor is obtained by subtracting the skilled labor from the total pool.

$LABSUP_{r,unskilled,t}=LAB_{r,p,t}-LABSUP_{r,skilled,t}$

Labor Demand: Equations

IFs economic model forecasts production in six economic sectors. IFs labor model computes the longer-term and shorter-term determinants of demand for skilled and unskilled labor (LABDEMS) for the production processes. The long-term drivers of labor requirement are technological progress or the lack of it. In the shorter-term wage affects the labor demand most. Wage in turn is affected by labor supply or skill shortage.

The IFs model divides economic activities into six economic sectors – agriculture, energy, materials, manufacture, services and information, and communication technologies. Workers in the IFs labor model are disaggregated into two skill types. While the skill composition varies by the technology used in the sector and starts tilting towards the more skilled with the progress in technology, absolute number of labors needed to produce the same output goes down with technological development for both skilled and unskilled labor. This is illustrated in the next figure which plots the changes in labor requirement against GDP per capita at PPP, a proxy for level of development. Agriculture is a much less skill-intensive process than the manufacture, however, with technological progress skill requirement improves rapidly in both sectors. The IFs labor model computes these labor requirement functions in the model pre-processor. As we have already described in the pre-processor section, the computation of these functions use GTAP data on employment by occupation and economic activity. Appendices 3 and 4 lists sector and occupation mapping between GTAP and IFs.

These functions are used to compute the labor coefficients (LABCOEFFS), i.e., number of skilled and unskilled labor needed to produce unit amount of output with the technology available, for which we use GDP per capita at PPP as a proxy.

$LABCOEFFS_{r,sk,s,t}=f(GDPPCP_{r})$

manufacture, services and ICTech) and the subscrip sk stands for skill categories with 1 denoting unskilled and 2 skilled. The labor coefficients obtained from the analytical functions require some adjustments to incorporate country deviations from the functions for various factors not captured in the regression relationship. The first of these adjustments is a gradual removal of impacts of short-run fluctuations in output and labor from the computation of labor coefficient. This adjustment is applied on the coefficients computed from the function. The equation below shows a simplified form of these computations.

$LabCoeffAdjFac_{r,k,s,t}=f(igdpr_{r,t=2},(LAB_{r,t=2}/LAB_{r,t=1}),(LABCOEFFS_{r,t}/LABCOEFFS_{r,t-1}))$

$LABCOEFFS_{r,sk,s,t}=LABCOEFFS_{r,sk,s,t}(1-LabCoeffAdjFac_{r,k,s,t})$

Model users can use a global parameter (labcoeffsm) to change the labor coefficients by skill level for any or all of the six sectors –

$LABCOEFFS_{r,sk,s,t}=LABCOEFFS_{r,sk,s,t}*'''labcoeffsm_{s,sk}'''$

To forecast the total labor demand, the labor coefficients (LABCOEFFS) are multiplied to the total projected output for each of the economic sectors. The forecast is adjusted for any discrepancy between data and model. The adjustment factor (LABDemsAdjFac) is computed as the initial ratio between the actual and computed employment. Actual employment is obtained from historical data (LABEMPS) processed using the GTAP database. The computed employment is obtained by multiplying the labor coefficients (LABCOEFFS) with the final output of the sector (VADD).

$LabDemsAdjFac_{r,s,sk}=LABEMPS_{r,s,sk,t=1}/(VADD_{r,s,t=1}*LABCOEFFS_{r,sk,s,t})$

The projected output is obtained by applying the growth rate (IGDPRCOR) on the sectoral value added from the previous year (VADD). The total labor demand is given by the product of the labor coefficients, projected output, demand adjustments and wage impacts (labwageimpactmul) and the number 1000 which adjusts the units for the equation. Wage impact comes from the level of unemployment and is computed in an equilibration process described in the next section. Model users can use a multiplicative parameter (labdemsm) to slide the demand upward or downward.

$LABDEMS_{r,s,sk,t}=1000*VADD_{r,s,t-1}*(1+IGDPRCOR_{r})*LABCOEFFS_{r,sk,s,t}*LabDemsAdjFac_{r,s,sk}*labwageimpactmul_{r,s,sk}*'''labdemsm_{r,s}'''$

Unemployment and Wage: Labor Market Equilibration

The IFs labor model balances the labor market through an equilibrium seeking algorithm rather than computing an exact equilibrium at each time step. We use an algorithm borrowed from the control systems engineering. This PID controller algorithm, described also in the IFs economic model documentation, works by computing corrective signals for equilibrating variables using the deviations of a buffer variable, for example unemployment rate (LABUNEMPR), from a target value. The signal is computed from two quantities, the distance of the buffer from the target and the current rate of change of the buffer. The computation is tuned with PID elasticities to avoid oscillations. The computed signal is applied on the variable/s which need to be balanced, for example, demand and supply in the event of a market equilibration, thus getting closer to a balance at each step of simulation. The target value for the buffer variable and the tuning parameters of the control algorithm are obtained through rules-of-thumb and model calibration. The IFs labor model uses unemployment rate (LABUNEMPR) as the buffer variable for the market equilibration of labor demand and labor supply. The multiplier (i.e., corrective signal) obtained from the PID is applied on the wage index (LABWAGEIND). Changes in wage indices comparative to the base year, moderated through a second PID controller, is used to compute the final signal (labwageimpactmul) that drives labor demand and labor supply. Even though the model forecasts labor demand by sector and skill, and computes labor supply for both skill types, the equilibration algorithm works over the entire pool of labor. In other words, we assume that the skills are replaceable across sectors and the lack (or abundance) of jobs affects skilled and unskilled persons equally.

At each annual timestep, the model computes the unemployment rate (LABUNEMPR) as the gap in between the total supply of labor (LAB) and the total demand. The gap (EmplGap) is expressed as a share of the total labor, the standard way to express unemployment rate.

$sumld=sum_{s,sk}LADEMS_{r,s,sk,t}$

$EmplGap=LAB_{r,t}*sumld$

$LABUMENPR_{r,t}=(EmplGap/LAB_{r,t})*100$

As the target value (LabUnEmpRateTar) for the PID controller that modulates unemployment rate we use either the historical unemployment rate or a ten percent unemployment rate when the historical rate is higher than ten. Model users can override the historical target through a model parameter (labunemprtrgtval).

$LABUMENPRi_{r,t}=LABUMENPR_{r,t}$

$LabUnempRateTarget_{r}=labunemptargetval_{r}$

$IfLabUnempRateTarget_{r}=0,LabUnempRateTarget_{r}=AMIN(LABUMENPRi_{r,t},10)$

Unemployment rate target, when it is different from the base year value, is reached gradually with a convergence period of forty years . The target rate is converted to count (LabUnEmplTar) to make it equivalent to the employment gap (EmplGap) computed earlier.

$LabUnEmplTar_{r}=LAB_{r,t}*ConvergeOverTime(LABUMENPRi_{r,t},0,100)$

The first order difference (Diffl1) between the target unemployment and the demand-supply gap is used to compute a second order difference (Diffl2) accounting for changes in the rate of movement. The two differences and the PID multipliers (elwageunemp1, elwageunemp2) are provided to the PID function (ADJSTR). Working age population (POP15TO65r,t) works as the scaling base of the PID controller. The controller algorithm gives a multiplier (mullw) that is used in the subsequent year to adjust wage.

$Diffl1_{t}=LabUnEmplTar_{r}-EmplGap$

$Diffl2_{t}=Diffl1_{t}-Diffl1_{t-1}$

$mullw_{r,t}=ADJSTR(POP15TO65_{r,t},Diffl1_{t},Diffl2_{t},elwageunemp1_{r},elwageunemp2_{r})$

Wage adjustments affect demand and supply with an increase in wage drawing demand downward and supply upward. The opposite affects occur with a downward movement of wage. The wage variable affected by the PID multiplier (LABWAGEIND) is an index initialized at one. We use an indexed rather than a dollar wage in the equilibration process to avoid affecting the process from other economic phenomena that affects wage, for example, a rise in real wage as GDP or the labor share of income grows.

$LABWAGEIND_{r,t=1}=1$

In the subsequent years of the model run, the wage index is first adjusted with the equilibration signal obtained from the unemployment rate PID controller in the previous period

$LABWAGEIND_{r,t=1}=LABWAGEIND_{r,t=1}*mullw_{r,t-1}$

A wage impact (labwageimpact) is then computed using the changes in the wage index relative to the base value. The impact is smoothed with a moving average algorithm.

$labwageimpact_{r}=labwageimpact_{r,t-1}*0.9+(1-LABWAGEIND_{r,t})*0.1$

The smoothed impact is used as the equilibration signal for labor supply. As we have already described in the section on labor supply, a small fraction of the impact (labwageimpact) is applied to the labor participation rate. The impact is scaled down to account for the slow pace of changes on the supply side.

$LABPARR_{r,p,t}=LABPARR_{r,p,t}*(1-labwageimpact_{r,t}*0.05)$

For the impacts of wage on labor demand we use a second PID multiplier as opposed to using the changes in wage index that we have done on the supply side. The second PID uses the wage index itself as the process variable and uses the base year value of 1 as the target. The reason we had to use this second PID is to control the pace at which wage disequilibrium can affect demand, especially in the event of an abrupt shock. The smoothing and scaling down that works on the supply side is not enough to control oscillations on the demand side.

$Diffl1_{t}=LABWAGEIND_{r,t=1}-1$

$Diffl2_{t}=LABWAGEIND_{r,t}-LABWAGEIND_{r,t-1}$

$mullw_{r,t}=ADJSTR(POP15TO65_{r,t},Diffl1_{t},Diffl2_{t},ellabwage1_{r},ellabwage1_{r})$

A second impact factor (labwageimpactmul) is computed using the correction signal from this second multiplier:

$labwageimpactmul_{r,t}=labwageimpactmul_{r,t-1}*mullw_{r,t}$

This impact factor is applied on the labor demand as described in the section on labor demand.

$LABDEMS_{r,s,sk,t}=LABDEMS_{r,s,sk,t}*labwageimpactmul_{r,t}$

Informal Labor

IFs forecast labor and GDP share of the informal sector. Informal labor forecast is not explicitly endogenized in the labor market though. They are rather driven by development, skill and regulatory factors[1]. However, the productivity and revenue impacts of changes in informality affects output and thus labor demand implicitly as a very distal driver.

References